Fourier Sine and Cosine Series
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Series Concept
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss the Fourier sine and cosine series, which are key to solving boundary value problems in partial differential equations.

How do we determine when to use sine or cosine series?

Great question! We typically use sine series for Dirichlet boundary conditions — where the function is set to zero at the boundaries. Conversely, we apply cosine series for Neumann conditions — where the derivative at the boundaries is zero.

So it's all about the boundary conditions?

Exactly! Remember the mnemonic 'DC for Dirichlet and NC for Neumann' to help with the association.
Deriving Fourier Sine and Cosine Series
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore how we can derive these series. For a function defined on [0, L], the Fourier sine series is expressed as a sum of sines...

Can you show an example of this?

Absolutely! If we have a function f(x) defined, the sine series can be defined as... Remember, the coefficients are crucial!

What if the function is not periodic?

That’s a good point! We often use piecewise continuous functions to ensure convergence.
Application in Engineering Problems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about applications. How do you think Fourier series helps in civil engineering?

It helps model things like temperature distribution, right?

Exactly! There’s an example where we solve the heat equation using a Fourier sine series...

Are there any specific engineering problems where one series is preferred over the other?

Yes, for instance, in heat conduction with fixed endpoints, we often use sine series.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The Fourier sine and cosine series represent a means to express periodic functions defined on a closed interval, specifically adapting to boundary conditions in scenarios such as Dirichlet and Neumann conditions. This conversion is crucial in civil engineering applications where solving PDEs is fundamental.
Detailed
Fourier Sine and Cosine Series
The Fourier sine and cosine series are essential tools in representing functions defined on the interval [0, L]. They allow engineers to address boundary conditions effectively when solving partial differential equations (PDEs). In cases where the boundary conditions are Dirichlet (where the function is zero at the boundaries), the sine series is appropriate. Conversely, in situations where Neumann conditions are applied (where the derivative is zero at the boundaries), the cosine series is more fitting.
This section explains how these series can be developed from periodic functions and emphasizes their significance in the context of PDE solutions relevant to various engineering problems such as heat transfer and fluid flow.
Youtube Videos
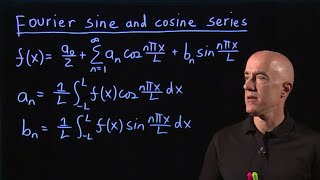








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Sine Series
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For functions defined on [0, L], we can define:
• Fourier sine series (odd extension)
These are used to match boundary conditions in PDE problems:
• Dirichlet BCs (zero at boundaries): Use sine series
Detailed Explanation
The Fourier sine series allows us to represent functions defined on the interval [0, L] as sums of sine functions. When we have boundary conditions that require the function to be zero at the boundaries (Dirichlet boundary conditions), the sine series is particularly effective. This is because sine functions naturally have a zero value at both ends of the interval, effectively matching these boundary conditions.
Examples & Analogies
Imagine tuning a guitar string. When you pluck the string, it vibrates and produces sound waves. If you imagine that the ends of the string are fixed (the boundaries), the vibrations can be represented using sine functions, which always start and end at zero — just like the ends of the guitar string.
Fourier Cosine Series
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Fourier cosine series (even extension)
These are used to match boundary conditions in PDE problems:
• Neumann BCs (zero derivative at boundaries): Use cosine series
Detailed Explanation
The Fourier cosine series provides another way to express functions defined on the interval [0, L]. This series is suitable for scenarios where boundary conditions require the function's derivative to be zero at the ends (Neumann boundary conditions). The cosine functions start at their peak value and can smoothly taper off to zero, making them suitable when the function itself doesn't need to be zero at the boundaries, but the slope does.
Examples & Analogies
Consider a smooth water surface in a pond. When a pebble is thrown in, the waves that ripple out from the point of impact can be thought of in terms of cosine functions, which smoothly rise and fall. Unlike sine waves, cosine functions can represent the situation where the height of the water surface is maximum at the start (the edge), tapering off smoothly toward the center, where the natural flow isn’t disturbed.
Boundary Conditions and Their Importance
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
These are used to match boundary conditions in PDE problems:
• Dirichlet BCs (zero at boundaries): Use sine series
• Neumann BCs (zero derivative at boundaries): Use cosine series
Detailed Explanation
Boundary conditions are crucial for solving partial differential equations (PDEs) as they define specific behavior at the boundaries of the domain. Dirichlet boundary conditions specify the value of a function at the boundaries, while Neumann boundary conditions specify the rate of change (derivative) at those boundaries. By selecting the appropriate Fourier series (sine for Dirichlet and cosine for Neumann), we can ensure that our solutions meet these requirements, leading to accurate interpretations of physical phenomena.
Examples & Analogies
Think about weather forecasting as a form of boundary condition application. Meteorologists consider temperature readings (like Dirichlet conditions) and the rate at which temperatures change (like Neumann conditions) at various locations on the map to predict how weather patterns evolve over a region. Just like they have specific data points to work with, engineers use sine and cosine series to accurately model systems under various conditions.
Key Concepts
-
Sine Series: A series used for functions with Dirichlet boundary conditions.
-
Cosine Series: A series used for functions with Neumann boundary conditions.
-
Boundary Conditions: Constraints set on a function at its boundaries which determine the type of Fourier series to use.
Examples & Applications
For a function defined as f(x) = 0 at x=0 and x=L, the Fourier sine series representation is utilized to model issues like heat transfer.
In a scenario with fixed endpoints and needing to maintain zero gradient at boundaries, a Fourier cosine series is implemented.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Sine at the edges is zero, Cosine gets zero slope, bring solutions with ease, how we work with hope.
Stories
Imagine a bridge where the temperature must stay below a certain point at both ends—sine waves help it cool uniformly like a steady breeze.
Memory Tools
DC = Dirichlet Conditions mean values fix; NC = Neumann Conditions mean slopes can't mix.
Acronyms
S.D. represents Sine for Dirichlet; N.C. is for Cosine a Neumann array!
Flash Cards
Glossary
- Fourier Sine Series
A representation of a function defined on [0, L] as an infinite sum of sine functions, typically used for Dirichlet boundary conditions.
- Fourier Cosine Series
A representation of a function defined on [0, L] as an infinite sum of cosine functions, typically used for Neumann boundary conditions.
- Dirichlet Boundary Condition
Boundary conditions where a function assumes specific values at the boundaries.
- Neumann Boundary Condition
Boundary conditions where the derivative of a function is specified at the boundaries.
Reference links
Supplementary resources to enhance your learning experience.
