Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Orthogonality Property
Unlock Audio Lesson
Today, we'll discuss the orthogonality property of eigenfunctions. Can anyone tell me what orthogonality means in the context of functions?
Does it mean that the functions are at right angles to each other?
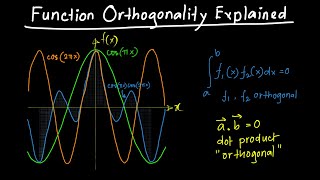
Good point, Student_1! Mathematically, it means the inner product of two different eigenfunctions is zero when integrated over a specified interval. For our case, it's the sine functions over [0, L].
So, what’s the formula for that?
The formula is: \( \int_0^L \sin\left(\frac{m\pi x}{L}\right) \sin\left(\frac{n\pi x}{L}\right) dx\). This integral equals zero when \( m \neq n \), ensuring unique contributions in our series expansion. It's essential for ensuring that each coefficient we calculate is accurate!
Why is this important for practical applications, like those in engineering?
Excellent question! The orthogonality ensures that the Fourier series can effectively represent complex functions. It guarantees that solutions we obtain for PDEs, such as temperature distributions or structural vibrations, are unique and stable.
So, to summarize this session, the orthogonality of eigenfunctions allows us to confidently compute Fourier coefficients, ensuring that our series solutions remain accurate and applicable.
Fourier Coefficients from Inner Products
Unlock Audio Lesson
Now, let’s delve into calculating Fourier coefficients using inner products. Can someone explain how we use the projection of a function onto an eigenfunction?
Do we take the function, multiply it by the eigenfunction, and integrate?
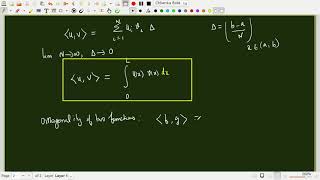
Absolutely, Student_4! The nth Fourier coefficient is given by: \( C_n = \frac{\langle f(x), \phi_n(x) \rangle}{\langle \phi_n(x), \phi_n(x) \rangle} \), where \( \langle f(x), \phi_n(x) \rangle \) is the inner product of the function and the eigenfunction.
What does the inner product tell us?
Great question! The inner product measures how much of the eigenfunction is in the function f(x), allowing us to find its coefficient in the Fourier expansion. This process is crucial for modal analysis in structural engineering.
Can you give us an example?
Sure! If we take a function f(x) and decompose it into its eigenfunction series, we can determine the specific contributions of each eigenfunction to represent f(x) accurately. Remember, these contributions must respect the orthogonality to maintain accuracy!
In summary, using inner products to find Fourier coefficients allows for an efficient decomposition of functions, ensuring that we construct accurate models in engineering applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the orthogonality property of eigenfunctions derived from Sturm–Liouville problems, which play a crucial role in computing Fourier coefficients. This orthogonality ensures the uniqueness and completeness of the Fourier series, providing a foundation for solving partial differential equations in engineering applications.
Detailed
Orthogonality and Eigenfunction Expansion
In this section, we delve into the concepts of orthogonality and eigenfunction expansion, pivotal in the context of Fourier series. The eigenfunctions, specifically the sine functions arising from Sturm–Liouville problems, are orthogonal over the interval [0, L]. This property is mathematically expressed as:
\[
\int_0^L \sin\left(\frac{m\pi x}{L}\right) \sin\left(\frac{n\pi x}{L}\right) dx = \begin{cases}
0, & m \neq n\
\frac{L}{2}, & m = n
\end{cases}
\]
This orthogonality is vital for determining Fourier coefficients used in representing functions as a sum of sine and cosine terms, ensuring that each function in the series contributes uniquely to the solution. Additionally, we introduce the inner product notion, where the projection of a function onto an eigenfunction determines the corresponding Fourier coefficient. Understanding these principles is crucial for applications in civil engineering, particularly when analyzing heat distribution, vibrations, and fluid flow.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Orthogonality Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The eigenfunctions {sin(nπx)} arising from Sturm–Liouville problems are orthogonal over the interval [0,L]:
\[ \int_{0}^{L} \sin(m\pi x) \sin(n\pi x) \; dx = \begin{cases} 0, & \text{if } m \neq n \ \frac{L}{2}, & \text{if } m = n \end{cases} \]
This orthogonality is crucial for computing Fourier coefficients and ensures the uniqueness and completeness of the series solution.
Detailed Explanation
The orthogonality property refers to how different eigenfunctions do not overlap in terms of their contributions over a specific interval, which, in this case, is from 0 to L. When you take the integral of two distinct sine functions (for different n values), the result is zero, indicating that these functions do not influence each other. However, if the two functions are the same (m=n), the integral equals L/2. This property is critical when calculating Fourier coefficients, allowing us to uniquely determine a function's representation in terms of these eigenfunctions. It guarantees that the representation is both unique (no other combination of functions will give the same result) and complete (any possible function can be represented).
Examples & Analogies
Imagine two musical notes played simultaneously. If the notes are different (like a C and a G), they sound harmonious and don't clash, just like orthogonal functions. If you play the same note twice, they amplify each other, resulting in a stronger sound, similar to how the integral equals L/2 for identical functions.
Fourier Coefficients from Inner Products
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let \( \phi_n(x) \) be the nth eigenfunction. Then the projection of f(x) onto \( \phi_n(x) \) (using the inner product) gives:
\[ \langle f(x), \phi_n(x) \rangle \]
\[ C_n = \frac{\langle f(x), \phi_n(x) \rangle}{\langle \phi_n(x), \phi_n(x) \rangle} \]
This inner product viewpoint forms the basis of modal analysis in structural engineering.
Detailed Explanation
In this part, the relationship between a function f(x) and the eigenfunctions \( \phi_n(x) \) is described through inner products, similar to measuring how much one function aligns with another. The expression \( C_n \) is essentially a coefficient that expresses how much of eigenfunction \( \phi_n(x) \) is present in the function f(x). It is derived by dividing the inner product of f(x) and \( \phi_n(x) \) by the inner product of \( \phi_n(x) \) with itself, ensuring you are scaling correctly based on the 'size' of the eigenfunction. This concept is crucial in fields such as structural engineering, where understanding the modes of vibration can lead to better designs and analyses.
Examples & Analogies
Think of this like measuring someone's participation in a group project where different members contribute differently. The inner product measures how much effort each member (eigenfunction) contributes toward the final project (function). The coefficient C_n reflects that member's contribution to the overall project, providing insights into their importance or role.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonality: The condition where different eigenfunctions contribute uniquely and do not overlap in the context of Fourier series expansion.
-
Fourier Coefficient: A value that indicates the contribution of an eigenfunction to the overall function representation, derived through inner products.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a boundary value problem where the temperature distribution in a rod is modeled using Fourier series expansion, demonstrating eigenfunction orthogonality.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Orthogonal functions, like two roads, don't cross, they contribute uniquely without any loss.
📖 Fascinating Stories
-
Imagine a dance floor where each dancer moves independently in their own space. Just like in Fourier series, each dancer contributes to the overall performance without stepping on each other's toes, representing the uniqueness of eigenfunctions.
🧠 Other Memory Gems
-
O.E.C. - Orthogonality Ensures Contributions. This helps to remember how orthogonality relates to Fourier coefficients.
🎯 Super Acronyms
FOC - Fourier Orthogonality Condition.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonality
Definition:
A property of functions where the integral of their product over a defined interval equals zero for distinct functions.
-
Term: Eigenfunction
Definition:
A special type of function that is associated with a particular linear operator or equation, often utilized in solving differential equations.
-
Term: Fourier Coefficient
Definition:
A coefficient derived from the inner product between a function and an eigenfunction, used in the representation of a function as a Fourier series.