Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonality
Unlock Audio Lesson
Today, we're going to discuss the concept of orthogonality, particularly in relation to eigenfunctions derived from Sturm-Liouville problems. Can anyone tell me what orthogonality means in a mathematical sense?
Isn't it about two functions being perpendicular to each other?
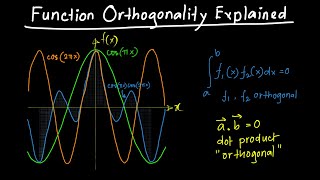
Exactly! When we say two functions are orthogonal, we mean their inner product is zero, which means they do not overlap in their contributions. This is crucial when working with Fourier series. Can you guys think of a common example of orthogonality?
Maybe the sine and cosine functions?
Great example! Similarly, the sine functions we are discussing here are orthogonal over the interval [0, L]. This property helps in simplifying computations of Fourier coefficients.
So it helps to make the calculations easier, right?
Yes, exactly! And this relationship is fundamental for the uniqueness and completeness of Fourier series solutions. Remember this as we move forward!
Mathematical Description of Orthogonality
Unlock Audio Lesson
Now, let’s dive into the math behind orthogonality. We can express it as an integral: the inner product of sine functions. Can someone recall the formula?
I think it's something like the integral of sin(mπx/L) times sin(nπx/L) from 0 to L?
Correct! The result is zero when m does not equal n, which illustrates the orthogonality. What do you think this property implies for Fourier coefficients?
It means we can find the coefficients separately without worrying about interference from other functions?
Absolutely! This is why we can use these orthogonal eigenfunctions to expand arbitrary functions in a unique way.
So, if we have a function, we can just project it onto these eigenfunctions?
Exactly! This projection helps us compute the Fourier coefficients effectively.
Applications of Orthogonality in Engineering
Unlock Audio Lesson
Let’s connect the dots between today’s mathematics and engineering. How do you think the orthogonality property applies in civil engineering?
I suppose it helps in analyzing vibrations in structures?
Yes! In structural engineering, the modal analysis relies heavily on understanding these orthogonal functions. What benefits do you think this brings to engineers?
It helps in predicting how structures might respond to different loads or forces without complex interactions?
Exactly! It simplifies understanding and designing for different environmental conditions by using distinct modes of vibration.
So the orthogonality property isn’t just theoretical; it has practical implications?
Indeed! Understanding this property allows engineers to create safer, more reliable structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Orthogonality of eigenfunctions, particularly the sine functions, plays a critical role in determining Fourier coefficients. This property ensures that different eigenfunctions do not interfere, allowing for the effective expansion of functions in terms of these orthogonal bases.
Detailed
Orthogonality Property
In the context of Sturm–Liouville problems, the eigenfunctions
$$ \left\{ \sin\left( \frac{n\pi x}{L} \right) \right\}_{n=1}^{\infty} $$
are orthogonal over the interval \([0,L]\). The inner product defined as:
$$ \int_0^L \sin\left( \frac{m\pi x}{L} \right) \sin\left( \frac{n\pi x}{L} \right) \, dx = \begin{cases}
0, & m \neq n \
\frac{L}{2}, & m = n
\end{cases} $$
is fundamental in the computation of Fourier coefficients. The property guarantees the uniqueness and completeness of the expansion, making it easier to represent any periodic function within the defined space. This foundational aspect enhances the modal analysis in structural engineering, where the projections of functions onto these eigenfunctions are critical.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Orthogonality of Eigenfunctions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The eigenfunctions {sin(nπx)/L} arising from Sturm–Liouville problems are orthogonal over the interval [0,L]:
\[ \int_0^L \sin\left(m\frac{\pi x}{L}\right) \sin\left(n\frac{\pi x}{L}\right) dx = \begin{cases} 0, & m \neq n \ 0, \ m=n \end{cases} \frac{L}{2} \]
Detailed Explanation
This chunk discusses the concept of orthogonality among eigenfunctions derived from Sturm–Liouville problems. In simpler terms, it tells us that when we take the integral (the sum of the products) of two different eigenfunctions (in this case, sine functions with different frequencies) over a specified interval ([0, L]), if the frequencies are not the same (m ≠ n), the integral equals zero. This means that these eigenfunctions do not 'interfere' with each other and are independent. If m equals n, then the integral equals L/2, reflecting that the function does have an intrinsic 'value' when paired with itself. This property of orthogonality is crucial in mathematics because it allows us to represent complex functions as sums of simpler ones without overlaps that could distort the representation.
Examples & Analogies
Think of orthogonal eigenfunctions like different musical notes. Each note can be played independently without mixing with others when played together in a chord. Just as you can separate the sounds of different notes to play a harmonious melody, you can use orthogonal eigenfunctions to piece together complex functions while ensuring that they don’t interfere with each other.
Importance of Orthogonality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This orthogonality is crucial for computing Fourier coefficients and ensures the uniqueness and completeness of the series solution.
Detailed Explanation
Orthogonality is very important when we use Fourier series in calculations. Because the eigenfunctions are orthogonal, we can confidently compute coefficients needed to describe different functions without overlap. This enables us to create unique and complete representations of functions when expressed as a series of these eigenfunctions. In other words, due to this property, the Fourier series can encapsulate all the different properties of a function, ensuring nothing is left out and that multiple functions aren't confused with each other in the series representation.
Examples & Analogies
Imagine trying to describe a complex painting. Each color (like each eigenfunction) plays a unique role without interfering with the others. If you know how much of each color to use, you can reproduce the exact painting. Similarly, with orthogonal functions, we can determine the precise coefficients to create an accurate representation of a function without mixing up the contributions from each eigenfunction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonality: The condition under which the inner product of two functions integrates to zero over a specified interval.
-
Eigenfunctions: Functions that arise in solving differential equations that form a basis for function expansion through orthogonality.
-
Fourier Coefficients: Scalar values computed from the inner products of a function and its orthogonal basis to represent the function in series form.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The sine functions \( \sin(\frac{n\pi x}{L}) \) are orthogonal over the interval [0, L], which means their integration leads to values of zero for differing indices.
-
In modal analysis for structures, eigenfunctions represent different vibrational modes, enabling engineers to predict responses accurately.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Sines that do not mix, they keep their own tricks, through inner product, they aren’t in the mix.
📖 Fascinating Stories
-
Imagine a dance floor where every dancer (eigenfunction) has their own unique space. They perform their moves without stepping on each other's toes because they are orthogonal – separate but harmonizing through music (Fourier series).
🧠 Other Memory Gems
-
Remember 'O.E.F.' for Orthogonality, Eigenfunctions, and Fourier – the essentials of Fourier series!
🎯 Super Acronyms
Use 'O.E.F.' to remember the key concepts
- Orthogonal functions
- Eigenfunctions
- and their role in Fourier Series.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonality
Definition:
The property of functions being perpendicular, indicated by the zero value of their inner product when integrated over a specified interval.
-
Term: Eigenfunctions
Definition:
Functions derived from a differential operator that satisfy specific conditions, forming an orthogonal basis for function expansion.
-
Term: Fourier Coefficients
Definition:
Coefficients derived from the inner products of a function with orthogonal eigenfunctions, used in generating Fourier series.
-
Term: SturmLiouville Problems
Definition:
A class of problems in which a linear differential operator is set, leading to an eigenvalue problem associated with eigenfunctions.