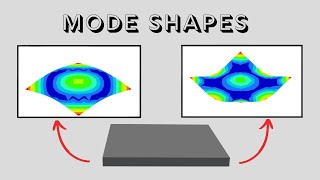
Mode Shapes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore mode shapes. First, can anyone tell me what a mode shape represents in a structural context?

Is it the way a structure vibrates?

Exactly, mode shapes indicate the specific patterns in which structures vibrate based on different frequencies. Can anyone give me an example of a mode shape?

Like the fundamental mode with a single half-wave?

Great example! Now, remember that higher modes, like the first overtone, show more complex patterns. These shapes are critical for predicting a structure's dynamic response.
Importance of Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand mode shapes, why do you think they are important for civil engineers?

They help us predict how buildings will respond to things like earthquakes?

Exactly! Knowing the natural frequencies and corresponding mode shapes enables us to design safer structures that can withstand dynamic loads.

So if a building vibrates too much in certain modes, it could fail?

That's correct! Excessive vibration can lead to structural failure, which is why analyzing these modes is essential.
Visualization of Mode Shapes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s think about visualizing mode shapes. How can Fourier series help us represent these shapes?

By breaking down complex shapes into sine and cosine components?

Right again! Each term in a Fourier expansion corresponds to a different mode shape. This breakdown helps identify the contribution of each vibrational pattern.

And the higher frequency components represent the more complex shapes?

Exactly! Over time, as the system settles, these higher modes diminish, leaving simpler patterns dominating the response.
Analyzing Temperature and Vibrations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's connect temperature distribution with vibrations. How might temperature affect mode shapes?

Different temperatures can change the material properties, affecting how it vibrates?

Exactly! Changes in temperature can alter stiffness and mass, impacting the natural frequencies and mode shapes we analyzed.

So engineers need to consider these factors in design?

Absolutely! Considering temperature along with vibrational modes leads to safer, more effective designs.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses mode shapes, which correspond to the unique vibrational patterns of structures resulting from eigenfunctions. Understanding mode shapes is critical in predicting how structures respond to dynamic loads, thereby aiding in design and analysis.
Detailed
Detailed Summary
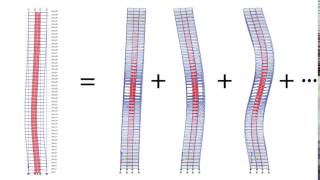
Mode shapes are essential concepts in structural analysis, particularly in understanding how structures such as beams and bridges behave under dynamic loads. Each eigenfunction corresponds to a specific vibrational mode of the structure. For instance, the fundamental mode (n=1) is characterized by a single half-wave, while the first overtone (n=2) has one full wave, and the second overtone (n=3) features two full waves. An understanding of these shapes is important as they dictate the natural frequencies of the system. Additionally, mode shapes illustrate how structures vibrate differently under various frequencies, affecting their overall performance and safety. This section emphasizes how Fourier expansions represent these vibrational modes and help in visualizing the dynamic behavior of structures as well as the decay of higher frequency effects over time.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fundamental Mode
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• n=1: Fundamental mode (single half-wave)
Detailed Explanation
The fundamental mode is the simplest form of vibration in a structure, represented by n=1. In this mode, the structure experiences one complete half-wave, which means there is one peak and one trough along its length. This is the lowest frequency at which the structure can vibrate, and often the most significant in terms of response.
Examples & Analogies
Imagine a jump rope being shaken at one end; the fundamental mode would look like the entire rope forming one large wave as it oscillates. It's the easiest movement for the rope, just like n=1 is for a structure.
First Overtone
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• n=2: First overtone (one full wave)
Detailed Explanation
The first overtone corresponds to n=2 and features one full wave in the length of the structure. This means that there are two peaks and two troughs along its length. This mode has a higher frequency than the fundamental mode and typically contributes significantly to the overall vibrational characteristics of the structure, particularly in dynamic loading scenarios.
Examples & Analogies
Think of a guitar string when you pluck it. The first overtone would create a sound with a frequency that is higher than the lowest sound (fundamental frequency) and would be heard as a sharper tone, just like how this mode provides a sharper response in a vibrating structure.
Second Overtone
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• n=3: Second overtone, etc.
Detailed Explanation
The second overtone is represented by n=3 and involves three half-waves along the length of the structure, resulting in three peaks and three troughs. This mode represents an even higher frequency and adds complexity to the behavior of the structure during vibration. These higher modes can interact with loads and lead to various vibrational behaviors.
Examples & Analogies
Returning to the jump rope analogy, shaking it in this second overtone would mean creating more complex waves, essentially waving it three times along its length. This increased motion demonstrates a more complex way in which a structure can respond to forces, similar to how musical instruments create different notes.
Vibrational Modes and Natural Frequency
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is analogous to a vibrating beam or bridge where each term in the Fourier expansion represents a different natural frequency.
Detailed Explanation
The concepts of mode shapes relate directly to the natural frequencies at which a structure can vibrate. Each mode is characterized by a specific frequency, and when a structure is subjected to dynamic forces, it may resonate at one of these natural frequencies, leading to amplified vibrational response.
Examples & Analogies
Think of how a swing set can sway. If you push it at just the right moments (the natural frequency), it swings higher and higher with less effort—this is resonance! Similarly, understanding the mode shapes helps engineers design structures that avoid resonating dangerously with certain frequencies.
Key Concepts
-
Mode Shape: The pattern of vibration specific to a structure at a given frequency.
-
Eigenfunction: A function that defines the relationship between certain physical properties and a structure's behavior.
-
Natural Frequency: The frequency at which a system tends to oscillate in the absence of any driving force.
Examples & Applications
The first mode shape of a cantilever beam is characterized by a single curve bowing upward.
A bridge oscillates in various modes during wind loading, with higher frequencies demonstrating shorter and more complex shapes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When buildings sway, they take a shape, Mode shapes arise as the vibrations take.
Stories
Imagine a violin string; when it's plucked, it vibrates in specific shapes, creating beautiful music. Each shape is a mode shape, representing a different frequency, just as different notes are played.
Memory Tools
Remember 'FMH' for fundamental, overtone, and higher modes: F is for the first simple shape, M is for the multiple waves of overtones, H for higher complexities.
Acronyms
Use 'M.O.D.E' to remember
for Mode
for Overtone
for Dynamics
for Eigenfunctions.
Flash Cards
Glossary
- Mode Shape
The specific pattern or shape in which a structure vibrates at its natural frequency.
- Eigenfunction
A non-zero function that, when acted upon by a linear operator, produces a scalar multiple of itself.
- Fundamental Mode
The first vibrational mode of a structure characterized by the simplest mode shape.
- Overtone
A mode shape whose frequency is a whole-number multiple of the fundamental frequency.
- Fourier Series
A way to represent a function as an infinite sum of sines and cosines.
Reference links
Supplementary resources to enhance your learning experience.
