Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Gaussian Elimination
Unlock Audio Lesson
Today, we will be discussing Gaussian elimination, a fundamental technique in solving linear systems. Can anyone tell me what linear systems are?
Are they sets of equations with multiple variables?
Exactly! These systems can be represented in matrix form as Ax = b. Now, what is our goal when we apply Gaussian elimination?
To find the values of the variables x?
Yes! We will eventually find x by transforming our matrix. Remember this acronym P.E.V.: 'Pivot, Eliminate, Verify'. It encapsulates the essence of our process.
What does 'pivot' refer to?
Great question! Pivoting involves selecting a leading coefficient to make other entries in the column below it zero. Let’s elaborate on that as we continue.
Forward Elimination
Unlock Audio Lesson
Now let's discuss forward elimination. This step transforms our system into an upper triangular form. Can anyone explain why this is beneficial?
So that we can use back substitution easily?
Exactly! By zeroing out the lower part of the matrix, we simplify our calculations. Who can recall the types of row operations we use?
We can swap rows, multiply rows by constants, and add or subtract rows.
Great! So as we perform these operations, we modify our augmented matrix step by step. It’s essential to maintain the equality of the equations.
Backward Substitution
Unlock Audio Lesson
Having reached upper triangular form, let’s explore backward substitution. Why do you think it’s called backward substitution?
Because we start from the last equation and move upward?
Exactly! We solve for the variables starting from the last equation where there’s only one variable. Can anyone give an example of how this works?
If we had an equation like 2x = 4, we would solve x = 2.
Perfect! Each variable found helps simplify the equation above it, demonstrating a clear order of operations.
Practical Applications
Unlock Audio Lesson
Let’s talk about why we should care about Gaussian elimination. How might engineers use this technique?
To analyze structures and ensure safety in designs!
Also, in modeling flows in civil engineering projects like drainage systems.
Absolutely! It’s integral in ensuring that systems behave predictively and correctly. So remember, whenever you encounter linear equations, think of Gaussian elimination!
Wrap-Up and Recap
Unlock Audio Lesson
To wrap up, what are the two major steps in Gaussian elimination?
Forward elimination and backward substitution!
And why do we perform these steps?
To find the solution to a linear system by transforming the matrix!
Exactly! Remember the mnemonic P.E.V., and you'll keep the process in mind. Great discussions today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
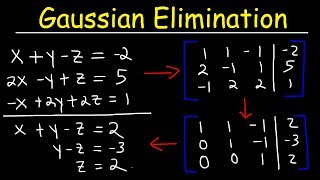
The Gaussian elimination method consists of two main steps: forward elimination, which transforms the given matrix into an upper triangular form, and backward substitution, which finds the solution to the equations. This systematic approach is foundational for solving linear systems.
Detailed
Gaussian Elimination
Gaussian elimination is an essential algorithm in linear algebra used to solve systems of linear equations. The process involves manipulating the augmented matrix of the system into upper triangular form and then performing back substitution to derive the solution.
Steps:
- Forward Elimination: This step modifies the original augmented matrix to reach an upper triangular form, allowing for easier calculation of the solutions.
- Backward Substitution: Once in upper triangular form, this step starts from the last equation and substitutes back to find the values of all unknowns sequentially.
The importance of Gaussian elimination cannot be understated as it lays the groundwork for various applications in fields such as engineering and mathematics, and it serves as the basis for more advanced algorithms like LU decomposition or Gauss-Jordan elimination.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Gaussian Elimination
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This method transforms the matrix into an upper triangular form using row operations, and then solves the resulting equations via back substitution.
Detailed Explanation
Gaussian elimination is a systematic method for solving systems of linear equations. The first step is to transform the matrix of coefficients into an upper triangular form. This means that all entries below the main diagonal of the matrix will be zero. After achieving this upper triangular form, the next step is known as back substitution, where you solve for the unknowns starting from the last equation and working your way up to the first equation. This method is efficient for finding solutions to linear equations as it simplifies the equations progressively.
Examples & Analogies
Think of Gaussian elimination like organizing a set of stacked boxes. Initially, they are jumbled up. Your goal is to sort them so that the largest boxes are at the bottom and the smaller boxes are stacked on top in such a way that any box can be accessed easily. Once sorted, you can easily identify which boxes to remove first to access smaller boxes underneath.
Steps of Gaussian Elimination
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Steps:
1. Forward elimination to convert to upper triangular form.
2. Backward substitution to compute unknowns.
Detailed Explanation
The process of Gaussian elimination consists of two main phases: forward elimination and backward substitution. During forward elimination, you perform row operations to create zeros below the pivot elements (which are the first non-zero numbers in each row). This process transforms the system of equations into an easier form. Afterward, backward substitution is applied. Here, starting from the last equation (which now only includes one variable), you substitute back up into the previous equations to find the values of all unknowns. Each step logically builds upon the last, leading to a complete solution.
Examples & Analogies
Consider solving a puzzle step-by-step, where each piece represents an equation. In the forward elimination step, you focus on creating space by removing pieces that don’t fit below each row. Once you have an organized area, you can start inserting pieces back into the puzzle, starting from the end and ensuring everything fits correctly as you work your way back to the beginning.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Gaussian elimination: A procedure for solving linear equations and finding solutions to linear systems.
-
Upper triangular matrix: A matrix form that simplifies solving linear equations after elimination.
-
Row operations: Actions taken to modify the rows of a matrix without changing the solution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Transform the system of equations into an augmented matrix and apply Gaussian elimination to solve for the variables.
-
Applying Gaussian elimination to a system with parameters will help analyze structural stability in engineering designs.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pivot the numbers, make zeros align, forward and backward, solutions will shine.
📖 Fascinating Stories
-
Once upon a time, in the land of Algebra, a brave student embarked on a quest to solve a series of linear equations using Gaussian elimination. Armed with their row operations and the magical techniques of forward elimination and backward substitution, they transformed complex systems into simple solutions.
🧠 Other Memory Gems
-
Remember 'P.E.V.' for Gaussian elimination: Pivot, Eliminate, Verify.
🎯 Super Acronyms
Use 'G.E.' to keep in mind Gaussian Elimination - where G is for Goal (to solve equations), and E is for Elimination (removing variables).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Gaussian elimination
Definition:
A systematic method for solving linear systems by transforming them into an upper triangular form, followed by back substitution.
-
Term: Upper triangular form
Definition:
A matrix form where all entries below the main diagonal are zero.
-
Term: Back substitution
Definition:
A method used after Gaussian elimination to find the values of the variables by substituting known values back into previous equations.
-
Term: Row operations
Definition:
Operations used in matrix manipulation, including row swapping, scaling, and row addition or subtraction.