Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Iterative Methods
Unlock Audio Lesson
Today we'll learn about iterative methods for solving large systems of linear equations. Why do you think we might need to use these methods instead of direct ones like Gaussian elimination?
Because direct methods might take too long for very large data sets?
Exactly right! Direct methods can be computationally expensive, especially with systems arising from applications in engineering. Iterative methods can provide solutions more efficiently.
What are some examples of iterative methods?
Great question. Some common examples include the Jacobi Method, Gauss-Seidel Method, and Successive Over-Relaxation. We'll go over each of these in detail today.
Jacobi Method
Unlock Audio Lesson
Let’s start with the Jacobi Method. Can anyone explain how it works in a simple way?
Is it where you update each variable sequentially based on previous values?
That's right! Each iteration uses only the values from the previous iteration for all variables. Do you remember the formula?
It's like you find each variable one at a time?
Exactly! Remember, convergence is usually guaranteed only if the matrix is diagonally dominant for the Jacobi method to be effective.
Gauss-Seidel Method
Unlock Audio Lesson
Now, let's look at the Gauss-Seidel Method. How does it improve upon the Jacobi Method?
By using updated values immediately during the iterations?
Exactly! This results in generally faster convergence. Can anyone articulate the new formula for this method?
I think it uses earlier updated values in the current iteration.
Correct! The Gauss-Seidel method utilizes the most recent solutions, leading to more efficient computations. Excellent work.
Successive Over-Relaxation (SOR)
Unlock Audio Lesson
Now let’s discuss the Successive Over-Relaxation method. What do you think makes this method unique?
It adds a relaxation parameter that can help speed up convergence?
Exactly! This parameter helps adjust how much of the new value contributes to the next iteration. Can anyone explain the SOR formula?
It's similar to Gauss-Seidel but includes the relaxation factor.
Well done! Understanding when and how to apply these methods can significantly improve your problem-solving skills in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Iterative methods are essential for handling large systems, especially in applications like finite element analysis. The Jacobi Method, Gauss-Seidel Method, and Successive Over-Relaxation are discussed, detailing how they improve efficiency for large datasets.
Detailed
Iterative Methods for Large Systems
For very large systems (e.g., in finite element grids), direct methods like Gaussian elimination become computationally intensive. Therefore, several iterative methods have been developed to provide solutions more efficiently:
1. Jacobi Method
This method updates the solution vector iteratively by solving for each variable based on values from the previous iteration:
\[ x^{(k+1)} = \frac{b - \sum_{j \neq i} a_{ij} x^{(k)}j}{a{ii}} \]
It converges slowly, primarily requiring the matrix to be diagonally dominant for convergence.
2. Gauss-Seidel Method
An improvement upon the Jacobi method, the Gauss-Seidel Method utilizes the most recent values as soon as they are available:
\[ x^{(k+1)} = \frac{b - \sum_{j < i} a_{ij} x^{(k+1)}j - \sum{j > i} a_{ij} x^{(k)}j}{a{ii}} \]
This method generally converges faster due to the updated values being used immediately.
3. Successive Over-Relaxation (SOR)
This method takes the Gauss-Seidel Method further by introducing a relaxation parameter \( \omega \), allowing for potential acceleration of convergence:
\[ x^{(k+1)} = (1 - \omega) x^{(k)} + \frac{\omega}{a_{ii}} \left( b - \sum_{j \neq i} a_{ij} x^{(k)}_j \right) \]
It is widely used in applications requiring robust solutions in various engineering fields.
Youtube Videos
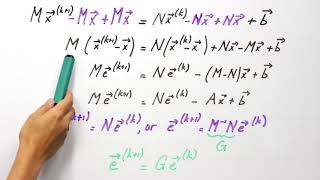
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Iterative Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For very large systems (e.g., in finite element grids), direct methods like Gaussian elimination become computationally intensive. Iterative methods are used instead:
Detailed Explanation
Iterative methods are techniques used to solve large systems of equations more efficiently than direct methods. When dealing with very large systems, such as those found in finite element analyses, direct methods can take too much time and computational power to yield results. Instead, iterative methods approach the solution incrementally, refining estimates until a satisfactory level of accuracy is reached.
Examples & Analogies
Think of iterative methods like tuning a musical instrument. Instead of hoping to get the perfect note on the first try (like a direct method that aims for an immediate exact solution), a musician tunes gradually, adjusting the pitch bit by bit until the desired sound is achieved. Here, each adjustment represents an iteration toward the final solution.
Jacobi Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
25.14.1 Jacobi Method
An iterative algorithm where each variable is solved using the values from the previous iteration:
x(k+1)= (b−∑a x(k)) / a(i)
Where the sum is taken over j where j ≠ i.
Converges slowly, and only if the matrix is diagonally dominant.
Detailed Explanation
The Jacobi Method is a simple iterative technique to find solutions to systems of linear equations. In this method, each variable is calculated using the most recent estimates of the other variables. The formula shows that for each next iteration, you compute the new value of x_i based on the values of other variables from the last iteration. This process continues until the changes are negligible, indicating convergence to a solution. However, the method relies on the matrix being diagonally dominant, meaning the absolute value of the diagonal entry in each row is greater than the sum of the absolute values of the other entries in that row.
Examples & Analogies
Imagine you and your friends are trying to evenly split a bill where everyone's contribution affects the final amount due. At first, everyone makes a guess based on previous amounts. After considering everyone's guesses, you readjust your amounts based on what everyone else has estimated. You repeat this process until you all agree on a fair split, similar to how the Jacobi Method adjusts values iteratively to converge on the final solution.
Gauss–Seidel Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
25.14.2 Gauss–Seidel Method
Improves over Jacobi by using updated values immediately in the iteration:
x(k+1)= (b−∑a x(k+1)−∑a x(k)) / a(i)
Where the first sum is over j where j < i, and the second sum is over j where j > i.
Detailed Explanation
The Gauss–Seidel Method enhances the Jacobi Method by making use of the most recent updates of the variables during iteration. This means that as soon as a new value for x_i is calculated, it can be used immediately to calculate the next value of x_i+1. This often leads to faster convergence compared to the Jacobi Method, as values are updated more frequently, allowing the iterations to incorporate new information as it becomes available.
Examples & Analogies
Consider a team collaborating on a project, where each member builds on the input from others. If one person finishes their part and shares it, the next person can immediately use that completion for their work instead of waiting for everyone to finish before starting again. This 'passing of ideas' in real-time is akin to the Gauss-Seidel Method, which uses the latest information to refine the solution more quickly.
Successive Over-Relaxation (SOR)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
25.14.3 Successive Over-Relaxation (SOR)
A modification of Gauss–Seidel introducing a relaxation parameter ω:
x(k+1)=(1−ω)x(k)+ω(b −∑a x(k)) / a(i)
Where the sum is over j where j ≠ i.
Used extensively in:
- Structural mesh solvers.
- Hydraulic modeling with boundary constraints.
Detailed Explanation
Successive Over-Relaxation (SOR) is a refined technique that builds on the Gauss–Seidel Method by introducing a relaxation factor (denoted ω). This factor helps accelerate convergence by allowing the solution to 'over-relax' or adjust more aggressively in the direction of the solution. If ω is set to a value greater than 1, it encourages larger steps toward the solution, potentially speeding up the convergence process. This method is especially effective in applications where the system of equations can have complex structures, like in structural analysis and fluid dynamics.
Examples & Analogies
Imagine a runner who is trying to get to a finish line faster. If they traditionally run (like simple iterations), they reach the end eventually. But by employing a strategy of sprinting (the over-relaxation), the runner can get closer to the finish line in fewer strides. In SOR, just like this runner, the iterative method takes bigger steps towards the solution, thus aiming to reach the desired outcome faster.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Iterative Method: A process for increasingly accurate approximations to solutions.
-
Jacobi Method: Updates all variables independently across iterations.
-
Gauss-Seidel Method: Incorporates immediately updated values for faster convergence.
-
Successive Over-Relaxation: Modifies Gauss-Seidel with a relaxation factor to potentially improve convergence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Jacobi Method to solve a system: x + y = 4 and x - y = 2.
-
Applying Gauss-Seidel Method to find values for x and y quickly in the same equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When matrices grow so large in a flurry, use iterative methods, don’t you worry!
📖 Fascinating Stories
-
Imagine a race where each runner takes a turn re-evaluating the leader. The one behind calculates based on the previous runner, much like Jacobi; but the current runner updates on the go, like Gauss-Seidel. And finally, with a special twist, one runner adjusts their pace based on how quickly they need to finish—the Successive Over-Relaxation.
🧠 Other Memory Gems
-
Recall 'J.G.S.' for 'Jacobi, Gauss-Seidel, SOR' to remember three key iterative methods.
🎯 Super Acronyms
Use 'IRD' for 'Iterative, Relaxation, Diagonal dominance' when remembering key features of these methods.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Iterative Method
Definition:
A technique for finding solutions to linear systems by repeatedly improving estimates.
-
Term: Jacobi Method
Definition:
An iterative algorithm that updates each variable based on the values from the previous iteration.
-
Term: GaussSeidel Method
Definition:
An iterative algorithm that updates variables immediately using the most recent values.
-
Term: Successive OverRelaxation (SOR)
Definition:
An enhancement of the Gauss-Seidel Method that introduces a relaxation parameter to accelerate convergence.