Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Systems of Linear Equations
Unlock Audio Lesson
Today, we’re diving into systems of linear equations. Can anyone tell me what defines a system of linear equations?
I think it’s a set of equations that have some common variables!
Exactly! They involve the same set of variables. Now, we can represent these systems compactly in matrix form. What does the general equation Ax = b stand for?
A is the matrix of coefficients, x is the vector of unknowns, and b is the right-hand side vector, right?
Correct! A crucial understanding for us in applied mathematics and engineering. Remember the acronym 'A for All, x for unknowns, and b for balance' — it helps keep their roles clear!
Types of Solutions
Unlock Audio Lesson
Now that we understand how to represent systems, let’s discuss the types of solutions they can yield. What can happen if a system is inconsistent?
It means it has no solution!
Right! And when it has exactly one solution, we call that consistent and independent. What about infinite solutions?
That’s when it’s consistent but dependent, because the equations aren't giving us new information!
Great insights! Let’s remember that with the phrase 'Inconsistent? No Solution!' for easy recall.
Conditions for Existence and Uniqueness
Unlock Audio Lesson
Let's now explore conditions for existence and uniqueness. Can anyone summarize when a system Ax = b has at least one solution?
It exists if Rank(A) equals Rank([A∨b]?)
Exactly! And if that solution exists, how do we determine its uniqueness?
If Rank(A) equals the number of unknowns, n!
Correct! To remember this easily, just think 'Rank Equals Number for Unique Results!'
Homogeneous and Non-Homogeneous Solutions
Unlock Audio Lesson
Now, let’s differentiate between homogeneous and non-homogeneous systems. Who can tell me what a homogeneous system is?
It’s when b equals 0!
Exactly, and the trivial solution always exists! What can you say about non-homogeneous systems?
They have a particular solution, plus solutions of the associated homogeneous system.
Great job! To remember this, think of 'Special First, Then General' for how solutions build on each other.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Systems of linear equations are foundational in engineering for modeling various phenomena. This section covers their mathematical representation in matrix form, explores solution types based on consistency and dependency, and outlines conditions for existence and uniqueness of solutions.
Detailed
System of Linear Equations
Systems of linear equations, prevalent in fields like engineering, consist of multiple equations with shared variables. The general form of such a system can be presented in a structured way using matrices.
- The foundational equation can be expressed as Ax = b, where:
- A is an m×n matrix of coefficients,
- x represents the vector of unknowns in Rn, and
- b denotes the right-hand side vector in Rm.
- Types of solutions include:
- No Solution: The system is inconsistent.
- Exactly One Solution: The system is consistent and independent.
- Infinitely Many Solutions: The system is consistent but dependent.
- The nature of solutions depends on the ranks of the matrix and its augmented form:
- Solutions exist if Rank(A) = Rank([A∨b]).
- For uniqueness, if a solution exists with Rank(A) = n, the matrix has full column rank, ensuring that the solution is unique. In square systems, this translates to det(A) ≠ 0 for uniqueness.
- Homogeneous systems (where b = 0) always contain at least the trivial solution x = 0, while non-homogeneous systems derive their solution from a particular solution plus the solutions of the associated homogeneous system.
Understanding these fundamentals paves the way for deeper insights into matrices, ranks, and their applications in solving real-world problems within engineering domains.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a System of Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A system of linear equations is a collection of equations involving the same set of variables. The general form of a system with m equations and n unknowns is:
a_11 x_1 + a_12 x_2 + ... + a_1n x_n = b_1
a_21 x_1 + a_22 x_2 + ... + a_2n x_n = b_2
...
a_m1 x_1 + a_m2 x_2 + ... + a_mn x_n = b_m
Detailed Explanation
A system of linear equations consists of multiple equations that share the same variables. In this system, each equation represents a linear relationship among the variables. The general setup includes 'm' equations and 'n' unknowns. Each equation can be expressed in the form where coefficients (like a_11, a_12, etc.) are multiplied by the variables (x_1, x_2, etc.), resulting in a constant (b_1, b_2, etc.).
Examples & Analogies
Think of a system of linear equations like a recipe with different ingredients. Each ingredient can influence the final dish, similar to how each variable influences the equations. If you have a recipe (equation) and you want to determine the correct quantities (variables) to achieve a desired taste (result), you're essentially solving a system of equations.
Matrix Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This can be compactly written in matrix form as:
A x = b
Where:
- A is an m×n matrix of coefficients.
- x ∈ R^n is the vector of unknowns.
- b ∈ R^m is the right-hand side vector.
Detailed Explanation
The system of linear equations can be conveniently represented using matrices. In this representation, 'A' is a matrix that contains all the coefficients of the variables from the system equations. The vector 'x' contains the unknown variables, and the vector 'b' represents the constants on the right side of the equations. This matrix form simplifies the mathematical handling of the equations and allows for efficient computations.
Examples & Analogies
Imagine you're organizing a sports tournament with teams, scores, and match-ups. Each match can be represented as a row in a table (matrix) where the columns might represent the scores of different teams (variables). By converting all this information into a structured format (matrix), you can easily analyze outcomes and determine standings, just like solving a system of equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Matrix Representation: Systems of linear equations are expressed in the form Ax = b, simplifying their analysis.
-
Types of Solutions: Systems can be inconsistent (no solution), independent (exactly one solution), or dependent (infinitely many solutions).
-
Existence and Uniqueness Conditions: Solutions exist when Rank(A) = Rank([A∨b]), with uniqueness determined by Rank(A) = n.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Consider the system of equations:
-
2x + 3y = 5
-
4x + 6y = 10
-
This system is dependent, having infinitely many solutions, represented as a line in R2.
-
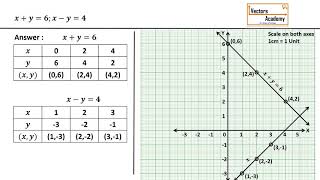
Example 2: The system:
-
x + y = 1
-
x - y = 2
-
This system is independent with a unique solution at the point (1.5, -0.5) in R2.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In equations, all aligned, to solve them, we must find; Solutions three: none, one, more - Rank conditions open the door!
📖 Fascinating Stories
-
Imagine a group of friends trying to meet at a common point (solution). Sometimes, they just can't (no solution), other times they meet once (unique solution), and sometimes they can gather in many places (infinitely dependent solutions).
🧠 Other Memory Gems
-
To remember ranks: R is for Ranks, A is for Augmentation, N is for Number of variables - RAN for 'Rank Equals Number'.
🎯 Super Acronyms
USE to remember conditions
- Unique solutions require 'U' for Rank(A) = n
- 'S' for solutions exist with Rank(A) = Rank([A∨b])
- and 'E' for equations forming a system.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: System of Linear Equations
Definition:
A collection of linear equations involving the same set of variables.
-
Term: Matrix
Definition:
A rectangular array of numbers or functions arranged in rows and columns.
-
Term: Homogeneous System
Definition:
A system of linear equations where the right-hand side is zero (Ax=0).
-
Term: NonHomogeneous System
Definition:
A system of linear equations where the right-hand side is non-zero (Ax=b).
-
Term: Rank
Definition:
The maximum number of linearly independent row or column vectors in a matrix.
-
Term: Unique Solution
Definition:
A solution to a system of equations that satisfies all equations precisely with no alternatives.
-
Term: Inconsistent System
Definition:
A system of equations that has no solutions.
-
Term: Dependent System
Definition:
A system of equations that has infinitely many solutions due to redundancy among equations.
-
Term: Independent System
Definition:
A system of equations where each equation provides unique information leading to a single solution.