Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Homogeneous Systems
Unlock Audio Lesson
Today, we will discuss homogeneous systems of linear equations. Can anyone tell me what the general form of such a system looks like?
Isn't it Ax = 0, where A is the matrix?
Exactly! In this equation, A is our coefficient matrix and x is the vector of unknowns. What do you think is the trivial solution?
I believe the trivial solution is when x equals zero?
Correct! x = 0 is always a solution. Now, when would we have non-trivial solutions?
If the rank of matrix A is less than the number of variables, right?
That's right! Remember, when Rank(A) < n, there are infinitely many non-trivial solutions. This leads us to the concept of the null space of A.
What is the null space, exactly?
Great question! The null space consists of all possible solutions to Ax = 0. And this space is crucial in understanding the solutions of linear systems.
To summarize, a homogeneous system always has the trivial solution. If Rank(A) < n, it also has other solutions, forming a vector subspace called the null space.
Characteristics of Homogeneous Systems
Unlock Audio Lesson
Now that we've covered the basics, let’s discuss the characteristics of these systems. Why does a homogenous system always have a solution?
Because of the trivial solution?
Exactly! The trivial solution x = 0 always exists. But what happens when Rank(A) equals n?
Then there would be a unique solution?
Close! In homogeneous systems, Rank(A) = n results in only the trivial solution—no other solutions exist. What could this mean practically?
It might indicate that the system constraints are such that only the trivial outcome is possible.
Great point! On the other hand, if Rank(A) < n, we encounter infinitely many solutions. Why does this matter?
It means there are many ways to satisfy the system’s equations?
Correct! These solutions form a vector subspace known as the null space of A, providing insight into the system's behavior.
In summary, in homogeneous systems, we either have only the trivial solution or infinitely many, significantly shaping our understanding of solutions in linear algebra.
Implications and Applications of Homogeneous Systems
Unlock Audio Lesson
Let’s discuss why understanding homogeneous systems is practically important. Can anyone think of an example?
Homogeneous systems are often used in structural analysis, right?
Indeed! Engineers often model structures using homogeneous equations to ensure stability. How do these equations help us?
They help in determining the conditions under which a structure can sustain loads without collapse.
Exactly! In homogeneous systems, the trivial solution can represent an equilibrium state. Also, what if we encounter a non-trivial solution?
That could mean there are several configurations that would also maintain stability.
Yes! Hence, these systems are essential in various engineering scenarios. Can anyone summarize the significance of null space again?
The null space contains all solutions to the homogeneous equation and tells us about the flexibility of solutions in the system.
Perfect! To conclude, homogeneous systems play a crucial role in mathematics and engineering, affecting how we model physical structures and analyze stability.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
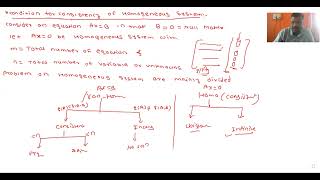
This section discusses homogeneous systems of linear equations, defined as Ax=0, focusing on the existence of solutions and the conditions that lead to trivial and non-trivial solutions. It also highlights the role of the null space or kernel of A in determining the nature of these solutions.
Detailed
Detailed Summary
In this section, we explore homogeneous systems of linear equations, which are represented in the form Ax = 0, where A is an m×n matrix and x is a vector of unknowns. A key characteristic of such systems is that they always include the trivial solution, x = 0. However, under certain conditions, specifically when the rank of matrix A (Rank(A)) is less than the number of unknowns (n), the system can also possess infinitely many non-trivial solutions.
This relationship is essential in linear algebra, as it relates to the concepts of vector spaces. In such cases, the set of all solutions forms what is known as the null space or kernel of the matrix A, which is a vector subspace of R^n. Understanding these properties is vital for applications in various engineering fields, where the behavior of systems can be modeled mathematically.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Homogeneous Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If b=0, the system is homogeneous:
Ax=0
Detailed Explanation
A homogeneous system of linear equations is defined as one where the right-hand side of the equation, denoted as 'b', is equal to zero. This means that the system can be expressed in the form Ax = 0, where A is the matrix of coefficients and x is the vector of unknowns. In this equation, the solution sought is the value of the vector x that satisfies the equation such that when multiplied by matrix A, it results in the zero vector.
Examples & Analogies
Think of it like a balance scale. When both sides of the scale are perfectly balanced, we can say that it’s at rest. In the same manner, when we say 'Ax = 0', we imply that there’s no net force acting on the unknown values (x), hence they balance out to zero.
Trivial Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The trivial solution x=0 always exists.
Detailed Explanation
In every homogeneous system, there is at least one solution known as the trivial solution, which is the zero vector (x = 0). This solution satisfies the equation Ax = 0 because if you multiply any matrix A by the zero vector, the result is always the zero vector. This is a fundamental property of linear algebra and confirms that the homogeneous system will always have a solution.
Examples & Analogies
Imagine you have a set of weights on a seesaw. If there are no weights on either side, the seesaw is balanced, representing the trivial case where the solution (x = 0) holds true. No additional weights or adjustments are needed.
Non-Trivial Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If Rank(A)<n, then there are infinitely many non-trivial solutions.
Detailed Explanation
A homogeneous system can have more than just the trivial solution. If the rank of matrix A (the maximum number of linearly independent column vectors in A) is less than the number of variables (n), this indicates that there are additional degrees of freedom in the solutions. Therefore, there exist infinitely many solutions known as non-trivial solutions. These solutions occur because the existence of free variables allows us to express some variables in terms of others, leading to multiple valid solutions.
Examples & Analogies
Consider a group of friends standing in a playground where they can choose any position as long as they remain in a certain zone. If there are fewer unique positions (rank) than friends (variables), they can shift around, creating many different configurations where they can still stay in the zone. Each configuration represents a different non-trivial solution.
Vector Subspace and Null Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution set forms a vector subspace of Rn called the null space or kernel of A.
Detailed Explanation
The collection of all solutions to a homogeneous system forms a mathematical structure known as a vector subspace. Specifically, this subspace is referred to as the null space (or kernel) of the matrix A. This space contains all possible solutions and has several important properties: it includes the zero solution, is closed under addition (the sum of two solutions is also a solution), and is closed under scalar multiplication (a solution multiplied by a scalar remains a solution). This structure helps in analyzing the solution space geometrically and algebraically.
Examples & Analogies
Think of the null space as a vast playground where the children (solutions) can roam freely in every direction as long as they respect the boundaries set by the specific rules (matrix A). Any group of children playing together in the playground can form different configurations (solutions) while always obeying those rules.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Homogeneous System: A system where the output vector is zero.
-
Trivial Solution: The solution where all unknowns are zero.
-
Null Space: The set of all possible solutions to the homogeneous equation.
-
Rank: The maximum number of linearly independent column vectors in the matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: The system 2x + 3y = 0 and x - y = 0 is homogeneous, having the trivial solution (0,0) and potentially other solutions.
-
Example 2: For a system Ax=0 where A has rank less than the number of variables, it represents a line or plane through the origin in vector space, indicating infinitely many solutions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a system that’s homogenous, the zero solution’s one to trust; if rank is low, then many will bust.
📖 Fascinating Stories
-
Imagine a bridge supported by cables. If no load is applied, its condition is stable (trivial solution), but with unexpected shifts in support, many configurations are still possible (non-trivial solutions).
🧠 Other Memory Gems
-
To remember the conditions for the solutions, use 'TRN': Trivial solution (always exists), Rank < number of Variables (infinitely many solutions), Non-trivial (when Rank < n).
🎯 Super Acronyms
Think 'HNR' for Homogeneous, Null Space, Rank when discussing homogeneous systems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Homogeneous System
Definition:
A system of linear equations where the right-hand side vector is zero, taking the form Ax = 0.
-
Term: Trivial Solution
Definition:
The solution x = 0, which always exists in a homogeneous system.
-
Term: NonTrivial Solution
Definition:
Any solution of the homogeneous system that is not the trivial solution (i.e., x ≠ 0).
-
Term: Rank
Definition:
The dimension of the vector space generated by the rows (or columns) of a matrix.
-
Term: Null Space
Definition:
The set of all vectors x that satisfy the equation Ax = 0, which forms a vector subspace of R^n.