Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Systems
Unlock Audio Lesson
Today, we're diving into the fascinating world of linear systems. A linear system is essentially a set of equations with the same variables. Can anyone give me the general form of such a system?
Is it something like ax + by = c?
Great! That's a simple example for two variables. In general, we express it as Ax=b, where A is a matrix of coefficients. Does everyone understand what A, x, and b represent?
A is the matrix of coefficients, x is the vector of unknowns, and b is the output vector, right?
Exactly! And understanding these terms is crucial as they lead us to analyze the system's solutions.
Types of Solutions
Unlock Audio Lesson
Now let's discuss the types of solutions one can encounter. Can anyone name them?
There can be no solutions, exactly one solution, or infinitely many solutions.
Correct! That's three distinct categories. Let's elaborate: 'No solution' means the system is inconsistent. What about when it’s consistent?
If it's consistent and independent, there’s only one solution. If it's dependent, there are infinitely many solutions.
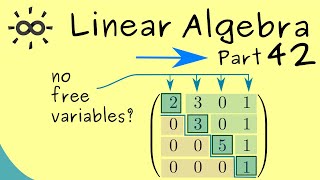
Well done! Remember, these classifications stem from the ranks of the matrix A and the augmented matrix [A|b].
Existence and Uniqueness of Solutions
Unlock Audio Lesson
Let's get into the nitty-gritty of existence and uniqueness! What condition do we need for at least one solution to exist?
You mentioned that Rank(A) must equal Rank([A|b].
Exactly! This equation tells us a lot. How about the uniqueness of that solution?
If the rank of A equals the number of unknowns, then there is a unique solution!
That's right! For square systems, this translates simply. If the determinant of A isn’t zero, we can be confident in our unique solution. Any questions about this?
General Form of Solutions
Unlock Audio Lesson
Now, let's articulate how we express solutions. For homogeneous systems, what does Ax=0 represent?
That’s the trivial solution!
Right! And if the rank of A is less than the number of variables, what can we say about the non-trivial solutions?
There are infinitely many non-trivial solutions that form a vector subspace!
Exactly! For non-homogeneous systems, if we find a particular solution, the general solution can be expressed by adding that particular solution to the homogeneous solution. It's fascinating how linear algebra describes complex systems!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Systems of linear equations play a critical role in various fields, especially in engineering. This section examines the conditions under which solutions exist, whether they are unique, and how to represent a general solution effectively.
Detailed
Detailed Summary
This section delves into the critical concepts of linear systems, exploring when solutions exist and under what conditions they can be described as unique or dependent. It begins by defining what a system of linear equations is, including its general mathematical formulation using matrices (i.e., Ax=b). The section also categorizes solutions into three discrete types: no solution (inconsistent), exactly one solution (consistent and independent), and infinitely many solutions (consistent but dependent).
It explains that the existence of a solution hinges on the rank of the coefficient matrix A equating to the rank of the augmented matrix [A|b]. Furthermore, if a solution exists and the rank matches the number of variables, then that solution is deemed unique. The treatment of homogeneous and non-homogeneous systems allows students to grasp how these solutions can be structured mathematically.
The significance of this understanding is embodied in practical engineering applications, where insights into the behavior of these systems contribute to the implementation of reliable computational methods in modeling real-life structures. Subsequently, different approaches for solving linear systems such as Gaussian elimination and LU Decomposition are highlighted, establishing a strong theoretical and practical foundation for further studies in this crucial area.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
System of Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
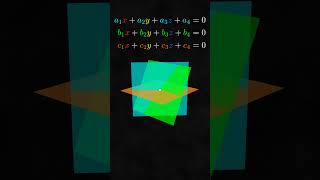
A system of linear equations is a collection of equations involving the same set of variables. The general form of a system with m equations and n unknowns is:
a x + a x + ⋯+ a x = b
11 1 12 2 1n n 1
a x + a x + ⋯+ a x = b
21 1 22 2 2n n 2
⋮
a x + a x + ⋯+ a x = b
m1 1 m2 2 mn n m
This can be compactly written in matrix form as:
Ax = b
Where:
- A is an m×n matrix of coefficients.
- x ∈ R^n is the vector of unknowns.
- b ∈ R^m is the right-hand side vector.
Detailed Explanation
In this chunk, we define a system of linear equations, which is a set of equations involving the same variables. For instance, in a situation where you have three equations and three unknowns, the system might look like three different ways to express a relationship between the same three variables. All of these equations can be organized into a matrix form, which simplifies calculations significantly in linear algebra. Here, 'A' represents the matrix of coefficients that corresponds to the variables 'x,' and 'b' represents the output of each equation.
Examples & Analogies
Imagine you're trying to solve a puzzle with different pieces that each represent a relationship (the equations). The variables are like the pieces that fit together to form the final picture (the solution). The matrix form is like organizing your puzzle pieces in a neat box, making it easier to see how they match up.
Types of Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A system of linear equations may have:
- No solution: The system is inconsistent.
- Exactly one solution: The system is consistent and independent.
- Infinitely many solutions: The system is consistent but dependent.
The nature of the solution depends on:
- The rank of the matrix A,
- The rank of the augmented matrix [A|b],
- The number of variables n.
Detailed Explanation
This chunk discusses the types of solutions a linear system can have. A system can either be inconsistent (no solution), have a unique solution, or have infinitely many solutions. The classification of the solutions is based on the rank of the matrices, which indicates the number of linearly independent rows (or equations) in the matrix. Essentially, rank helps us understand how much information we have in our equations, and consequently, what kind of solutions we can expect.
Examples & Analogies
Think of a college admission process as an analogy for these solutions. If the criteria (equations) don't match (inconsistent), no one can get in. If the school accepts one student who meets all requirements (one unique solution), that's straightforward. But if many students meet the criteria (infinitely many solutions), the school might have various ways to choose among eligible candidates.
Conditions for Existence of a Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A system Ax = b has at least one solution (i.e., it is consistent) if and only if:
Rank(A) = Rank([A|b])
If this condition is not satisfied, the system has no solution.
Detailed Explanation
This chunk states that for a linear system to have at least one solution, the rank of the coefficient matrix must equal the rank of the augmented matrix. In simpler terms, this means that the information (rank) contained in the coefficients needs to match the information in the entire system, including the outputs. If they do not match, it indicates that the equations contact contradictory information, resulting in no solutions.
Examples & Analogies
Consider trying to find a meeting time for a group of people with conflicting schedules. If their available times don't overlap (the ranks don't match), no time can be set (no solution). But if at least some schedules align (ranks match), a time can be found.
Conditions for Uniqueness of Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a solution exists and the rank of A equals the number of unknowns n (i.e., the matrix is of full column rank), then the solution is unique.
If Rank(A) = n, then the system has a unique solution.
In other words:
- For square systems (m = n): If det(A) ≠ 0, the system has a unique solution.
- For rectangular systems (m ≠ n): Use rank conditions.
Detailed Explanation
Here, we explore when a system has a unique solution. If the rank of the coefficient matrix matches the number of unknowns, the system will have a unique solution. For square systems (same number of equations as unknowns), if the determinant of the matrix is not zero, this further confirms uniqueness. In contrast, for systems with a different number of equations and variables, we rely on rank conditions to determine the uniqueness of solutions.
Examples & Analogies
Think of trying to navigate a new city with a GPS (the equations) that only provides one route to your destination (the unique solution). If there are multiple paths that might lead you there (more variables), the conditions must line up so that you trust the GPS directions and don’t get lost.
General Form of Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Homogeneous Systems
If b = 0, the system is homogeneous:
Ax = 0
- The trivial solution x = 0 always exists.
- If Rank(A) < n, then there are infinitely many non-trivial solutions.
- The solution set forms a vector subspace of R^n called the null space or kernel of A.
Non-Homogeneous Systems
For b ≠ 0, if a particular solution x_p exists, then the general solution is given by:
x = x_p + x_h
Where:
- x_p: A particular solution.
- x_h: General solution of the homogeneous system Ax = 0.
This means every solution of the non-homogeneous system is a sum of one particular solution and all solutions of the associated homogeneous system.
Detailed Explanation
This chunk presents the general forms of solutions for both homogeneous and non-homogeneous systems. A homogeneous system has a solution of zero and potentially more if the rank condition is met. Non-homogeneous systems build upon a known solution and add to it the solutions from the associated homogeneous system. This structure helps organize and understand the variety of solutions that can exist.
Examples & Analogies
Think of a chef preparing a dish (the particular solution) and then adding spices and herbs (the solutions of the homogeneous system) to enhance flavor. No matter the dish's base, the additional flavors (non-homogeneous solutions) create a unique experience, yet simultaneously stem from a consistent foundation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Systems: Equations involving the same variables; expressed in the form Ax=b.
-
Types of Solutions: Systems can be inconsistent (no solution), consistent and independent (unique solution), or consistent and dependent (infinitely many solutions).
-
Existence of Solutions: Rank(A) must equal Rank([A|b] for at least one solution to exist.
-
Uniqueness of Solutions: If Rank(A) equals the number of variables, then uniqueness is assured.
-
General Solution: Can be expressed as a combination of particular and homogeneous solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For the linear system represented by 2x + 3y = 6 and 4x + 6y = 12, the system is dependent and has infinitely many solutions.
-
The linear equation x + 2y = 4 has a unique solution at (4, 0) assuming proper rank conditions are satisfied.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a system of lines, when they cross just right, You'll find a unique solution in plain sight.
📖 Fascinating Stories
-
Imagine three friends trying to meet at a café. If their paths never intersect, they have no solution; if they meet precisely at one point, that’s unique; if they can continuously join forces, they create infinite possibilities.
🧠 Other Memory Gems
-
For no, one, or many solutions, remember: 'NiOs CLog' (No solutions, One solution, Many solutions Classified Logically).
🎯 Super Acronyms
Existence and Uniqueness = E.U.; think of 'Every Unique' as you connect solutions!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear System
Definition:
A collection of linear equations involving the same set of variables.
-
Term: Matrix
Definition:
A rectangular array of numbers, symbols, or expressions arranged in rows and columns.
-
Term: Matrix Rank
Definition:
The maximum number of linearly independent row vectors in a matrix.
-
Term: Homogeneous System
Definition:
A system of linear equations where the output vector b is zero.
-
Term: NonHomogeneous System
Definition:
A system of linear equations where the output vector b is non-zero.
-
Term: Determinant
Definition:
A scalar value that can be computed from the elements of a square matrix that provides insight into the matrix's properties.