Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Gauss–Jordan Elimination
Unlock Audio Lesson
Today, we'll discuss Gauss–Jordan elimination. This method modifies Gaussian elimination by converting matrices to reduced row echelon form, or RREF, which allows for direct reading of solutions. Can anyone explain why this might be beneficial?
It saves time by eliminating the need for back substitution!
Exactly! By getting to RREF, we make it much easier to isolate each variable. Let's also remember the acronym RREF: Reduced Row Echelon Form. This will help us recall its significance.
What are the actual steps involved in performing this elimination?
Good question! We'll first create an augmented matrix, perform row operations, and interpret the results. Let’s take a closer look at each.
Row Operations in Gauss–Jordan Elimination
Unlock Audio Lesson
In Gauss–Jordan elimination, we utilize three main row operations: row swapping, scaling, and row addition. Can anyone provide an example of when we might need to do these?
We would swap rows if one of the pivot positions is zero, right?
Correct! Row swapping helps us get a leading coefficient in place. Scaling adjusts rows to make the leading coefficients 1. Does anyone know what happens next?
We need to eliminate other entries in that column!
That's right! Through these operations, we aim to simplify the matrix until we achieve the RREF.
Interpreting the RREF
Unlock Audio Lesson
Once in RREF, how do we determine if a solution exists and what it is?
We look for any rows that imply inconsistency, like having a zero row equaling a non-zero number.
Exactly! If there are no inconsistencies, the solutions for each variable can be directly read from the matrix. Can someone explain how this might look?
If we see leading 1s in every column corresponding to variables, it shows we have a unique solution!
Well put! Understanding how to read RREF is key to solving linear systems effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores Gauss–Jordan elimination, highlighting how this augmented version of Gaussian elimination allows matrices to be transformed into RREF without the need for back substitution. Understanding this technique is crucial for engineers and mathematicians when dealing with linear systems.
Detailed
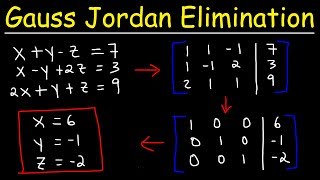
Gauss–Jordan Elimination
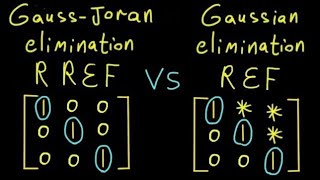
Gauss–Jordan elimination is an advanced form of the Gaussian elimination method used for solving systems of linear equations. This technique allows one to transform a matrix into reduced row echelon form (RREF), which simplifies the process of finding solutions to linear systems significantly. While traditional Gaussian elimination leads to an upper triangular matrix requiring back substitution, Gauss–Jordan elimination completes the process in a single step by eliminating all variables one directly after the other and producing a matrix form from which solutions can be read immediately.
The procedure begins with the construction of an augmented matrix from the equations involved. Through a series of row operations, the matrix is manipulated to achieve RREF. At this stage, each leading coefficient is 1 and is the only non-zero entry in its column. The simplicity of RREF makes it evident whether a solution exists and what the solution is in terms of the variables. This method is particularly useful in various applications, such as computer algorithms, engineering, and mathematical modeling.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Gauss–Jordan Elimination
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a modified version of Gaussian elimination that converts the matrix to reduced row echelon form (RREF), allowing the solution to be read directly without back-substitution.
Detailed Explanation
Gauss–Jordan elimination is a technique used to simplify a matrix for solving systems of linear equations. Unlike Gaussian elimination, which transforms a matrix into an upper triangular form, Gauss–Jordan elimination goes a step further to create a reduced row echelon form (RREF). In RREF, each leading entry of a row is 1, and is the only non-zero entry in its column. This means you can read off solutions directly from the matrix without needing to perform back-substitution. This makes it a very efficient method for finding solutions to linear systems.
Examples & Analogies
Think of Gauss–Jordan elimination like organizing a bookshelf. Instead of just stacking books in a row (like Gaussian elimination), you arrange them in such a way that each shelf has a clear title (the leading 1) and each title is unique to that shelf (only one non-zero entry per column). This makes it easier to find exactly what you need without digging through piles of books.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Gauss-Jordan Elimination: A method that allows direct retrieval of solutions from row-reduced matrices.
-
Row Operations: Fundamental manipulations applied to matrix rows during elimination.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of solving a linear system using Gauss–Jordan elimination resulting in RREF.
-
Demonstrating how inconsistency arises through an augmented matrix leading to a row implying no solution.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To eliminate in rows we play, swap, scale, and add all day.
📖 Fascinating Stories
-
Imagine a baker organizing his ingredients in rows, swapping what he needs, adjusting quantities, and combining flavors until he has the perfect recipe — this is like applying Gauss–Jordan elimination to solve equations!
🧠 Other Memory Gems
-
Remember the phrase 'Swap, Scale, Add' to recall the row operations in Gauss–Jordan.
🎯 Super Acronyms
WRAP - Write the matrix, Row reduce, Analyze, Print the solution.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reduced Row Echelon Form (RREF)
Definition:
A matrix form where every leading coefficient is 1, and is the only non-zero entry in its column.
-
Term: Row Operations
Definition:
Operations applied to the rows of a matrix, including row swapping, scaling, and row addition.