Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Singular Matrices
Unlock Audio Lesson
Today, we are diving into singular matrices. A square matrix is called singular if its determinant is zero. Can anyone tell me what that means for our system of equations?
It probably means the matrix can’t be inverted, right?
Exactly! And when a matrix is singular, that might lead us to have no solution or infinitely many solutions. This leads us to explore the solutions of the associated linear system. Can someone give an example of when we might encounter a singular matrix?
Maybe in systems with redundant equations?
Great example! Redundant equations can lead us to this scenario. Remember, whenever the determinant is zero, we’re in the territory of singular matrices.
Understanding Ill-Conditioned Systems
Unlock Audio Lesson
Now, let’s shift to ill-conditioned systems. What do we mean by that term?
I think it refers to systems that react a lot to tiny changes in parameters?
Correct! In an ill-conditioned system, small changes in coefficients can lead to significantly large errors in the solutions. This property is measured using the condition number of the matrix. Does anyone know how that is calculated?
Is it that κ(A) = ||A|| * ||A⁻¹||?
Spot on! If κ(A) is much greater than one, we say the system is ill-conditioned. Can you think of why this would matter in engineering?
It could lead to unreliable models or unsafe designs in engineering!
Exactly, and mitigating these issues is essential. We will discuss remedies shortly.
Remedies for Singular and Ill-Conditioned Systems
Unlock Audio Lesson
To address the challenges we face with singular and ill-conditioned systems, there are several techniques we can employ. What are some strategies you think we could use?
Using pivoting in Gaussian elimination might help!
Great suggestion! Pivoting aids in reducing numerical errors. Improving numerical precision is another method. Can you think of other strategies?
We could reformulate the equations or model to avoid these issues?
Exactly! Reformulating models can significantly enhance stability. In summary, handling singularity and ill-conditioning is vital in ensuring our engineering models are reliable.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we define singular matrices as those with a determinant of zero, indicating non-invertibility, which can lead to no solutions or infinitely many solutions. Additionally, we explore ill-conditioned systems, which are sensitive to changes in data, thereby impacting solution precision. Remedies for these issues, such as pivoting and improved numerical precision, are also discussed.
Detailed
Singular and Ill-Conditioned Systems
In the realm of linear systems, understanding singular and ill-conditioned matrices is vital for numerical stability. A singular matrix A is characterized by its determinant being zero (det(A) = 0). This condition means that such a matrix does not possess an inverse, leading to two potential outcomes for the associated linear system: it may either have no solutions (inconsistent) or infinitely many solutions (dependent).
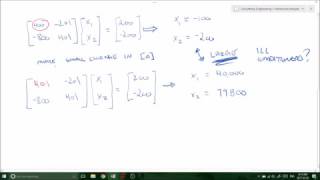
Ill-conditioned systems, on the other hand, are those that exhibit a high sensitivity to small changes within their coefficients or data inputs. This sensitivity is quantified by the condition number of the matrix, expressed as κ(A) = ||A|| * ||A⁻¹||. If the condition number is significantly greater than one (κ(A) ≫ 1), the system is deemed ill-conditioned, while a condition number close to one indicates a well-conditioned matrix.
Ill-conditioned systems frequently arise in structural engineering applications, especially within statically indeterminate structures or the modeling of complex geometries such as long-span bridges. Remedies for dealing with these issues include applying pivoting techniques during Gaussian elimination, improving the numerical precision of the data, or reformulating the model to enhance stability. By addressing singularity and ill-conditioning, we ensure that our models remain both solvable and reliable in engineering contexts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Singular Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A matrix A is singular if det(A)=0. In such cases:
- The system may have no solution or infinitely many solutions.
- The matrix is not invertible.
Detailed Explanation
A singular matrix is one whose determinant is zero, meaning it cannot be inverted. This situation arises because the rows (or columns) of the matrix are linearly dependent, which indicates that some equations in the system do not provide unique information. As a result, when solving Ax=b, the system may either not have a solution at all (inconsistent) or have an infinite number of solutions (dependent). Understanding this concept is crucial because it signifies limitations in finding a unique solution to linear systems.
Examples & Analogies
Imagine trying to find the intersections of two lines that are the same or parallel; if they are the same (infinite solutions), you can never pinpoint just one intersection. If they are parallel (no solution), they simply won't meet. This illustrates how singular matrices lead to similar scenarios in linear equations.
Ill-Conditioned System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An ill-conditioned system is highly sensitive to small changes in coefficients or data, leading to large errors in the solution.
This is measured by the condition number of matrix A:
κ(A)=∥A∥⋅∥A−1∥
- κ(A)≫1: Ill-conditioned
- κ(A)≈1: Well-conditioned
Such systems are common in:
- Statically indeterminate structures with close-to-parallel constraints.
- Long-span bridge modeling.
Detailed Explanation
An ill-conditioned system is one that reacts dramatically to slight changes in the input data used to create the equations. This sensitivity can lead to solutions that vary widely, even with minor modifications in the parameters, making the results unreliable. The condition number κ(A) is a key indicator of this sensitivity: a much larger than one value indicates instability. Engineers and mathematicians need to be aware of this issue to ensure their models provide reliable data, especially in critical fields like civil engineering.
Examples & Analogies
Think of an ill-conditioned structure; if you were building a bridge and each tiny error in measurement leads to structural issues, it's like trying to balance a pencil on its tip—any little breeze (data change) will knock it over. Knowing how sensitive your design is can help you make better decisions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Singular Matrix: A matrix with a determinant of zero, indicating potential infinitely many solutions.
-
Ill-Conditioned System: A system where small changes in input values yield large variations in output solutions.
-
Condition Number: A ratio indicating the sensitivity of a matrix, critical for assessing stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A system of equations represented by a matrix with zero determinant could lead to infinitely many solutions, such as when two equations are duplicates.
-
An example of an ill-conditioned system is one where the coefficients are nearly identical, leading to numerical inaccuracies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A singular matrix, oh what a sight, with zero determinant, it won't take flight.
📖 Fascinating Stories
-
Imagine you’re building a bridge with precise measurements. If your calculations are off slightly due to an ill-conditioning, it could lead to disastrous consequences, just like crossing a shaky bridge.
🧠 Other Memory Gems
-
To remember factors of ill-conditioning, think of 'SENSE': Sensitivity, Errors, Numerical instability, Statically indeterminate, and Equations.
🎯 Super Acronyms
S.I.N.E.
- Singular
- Ill-conditioned
- Non-invertible
- Error-prone.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Singular Matrix
Definition:
A matrix that has a determinant of zero, indicating it is non-invertible.
-
Term: IllConditioned System
Definition:
A system sensitive to small changes in coefficient values, leading to large errors in solutions.
-
Term: Condition Number (κ)
Definition:
A measure of sensitivity of a matrix, calculated as κ(A) = ||A|| * ||A⁻¹||.