Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Rank
Unlock Audio Lesson
Welcome, everyone! Today, we delve into the Rank-Nullity Theorem. Can anyone tell me what 'rank' refers to in the context of a matrix?
Is it the number of linearly independent rows or columns in the matrix?
Exactly! The rank of a matrix reflects how many of its rows or columns are linearly independent. This tells us about the dimension of the image of the matrix. Remember, a high rank indicates more information captured in those vectors. Let’s explore why this is important.
Right! So, a higher rank means more solutions possible?
Not quite! A higher rank often means fewer solutions exist, especially when the rank is equal to the number of variables. Let's explore this further.
Does that imply that if rank is less than the number of variables, there could be infinite solutions?
That's exactly right! If rank is less than the number of variables, it leads us to infinite or no solutions.
Understanding Nullity
Unlock Audio Lesson
Now, let’s discuss nullity. Who can define it for me?
Isn’t it the dimension of the null space of the matrix? The solutions to Ax=0?
Good job! Nullity measures the dimension of the solution space for the homogeneous equation. It's vital because it directly influences the total number of solutions our system can have.
So, if we have a nullity greater than zero, does that mean infinite solutions are likely?
Exactly! A nullity greater than zero implies infinite solutions because there exists at least one non-trivial solution to Ax = 0.
How can we visualize that in terms of the Rank-Nullity Theorem?
Great question! The theorem shows that the combination of rank and nullity gives us the total number of variables. So, if one increases, the other must decrease to maintain the balance!
Application of the Rank-Nullity Theorem
Unlock Audio Lesson
Let’s put this into practice. If we have a matrix \( A \) with \( ext{Rank}(A) = 3 \) and the matrix has 5 columns, what is its nullity?
So applying the theorem, \( 3 + ext{Nullity}(A) = 5\) would mean \( ext{Nullity}(A) = 2 \).
Perfect calculation! This means there are two dimensions in the solution space for \( Ax=0\). Can anyone apply this insight to a real-world situation or example?
In engineering designs, if we have more variables than the rank, it suggests multiple feasible options in system designs!
Well said! This flexibility is crucial in practical applications like civil engineering for solving complex systems. Remember, balancing rank and nullity leads to valuable insights on the behavior of the system.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elaborates on the Rank-Nullity Theorem, which states that the sum of the rank and nullity of a matrix equals the number of its columns. It highlights the significance of these dimensions in understanding the solutions of linear systems, particularly in describing the image and null space of the matrix.
Detailed
Rank and Nullity Theorem
The Rank-Nullity Theorem is a pivotal theorem in linear algebra that provides a relationship between two key properties of a matrix: its rank and its nullity. For an \( m \times n \) matrix \( A \), the theorem states:
\[ \text{Rank}(A) + \text{Nullity}(A) = n \]
Where:
- Rank(A) is the dimension of the image of the matrix \( A \) (i.e., the number of linearly independent columns).
- Nullity(A) is the dimension of the null space (or kernel) of the matrix \( A \), representing the number of solutions to the homogeneous equation \( Ax=0 \).
This theorem allows us to deduce critical information about the solutions of the linear system \( Ax = b \) by understanding the rank and nullity of the matrix involved. If the rank is equal to the number of variables, then the system has a unique solution. However, if the rank is less than the number of variables, this leads to different scenarios such as infinitely many solutions or no solution at all. It emphasizes the interplay between the structure of the matrix and the nature of solutions it can yield.
Youtube Videos
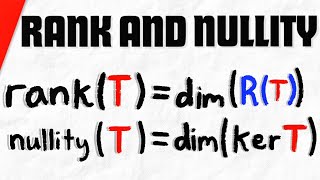
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Rank and Nullity Theorem Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For an m×n matrix A, the Rank–Nullity Theorem states:
Rank(A) + Nullity(A) = n
Where:
- Rank ≡ dim(Image of A)
- Nullity ≡ dim(Null space of A)
Detailed Explanation
The Rank-Nullity Theorem is a crucial result in linear algebra that applies to any matrix A with 'm' rows and 'n' columns. It states that the sum of the rank of a matrix (the dimension of its image, or the number of linearly independent columns) and the nullity of the matrix (the dimension of the null space, or the number of solutions to the equation Ax=0) equals the total number of columns 'n'. This means that if you know the rank of a matrix, you can easily calculate the nullity, and vice versa.
Examples & Analogies
Imagine a library where the total number of books is represented by 'n'. Each book can either be checked out or is available on the shelf. The rank would represent the number of unique books that are currently available (the shelves), while the nullity would represent the number of books that are checked out (the ones not available on the shelves). According to the Rank-Nullity Theorem, the total number of books 'n' is simply the sum of the books available and the books checked out.
Understanding Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Rank ≡ dim(Image of A)
Detailed Explanation
In the context of the Rank-Nullity Theorem, 'Rank' refers to the dimension of the image of the matrix A. This represents the maximum number of linearly independent column vectors in A. The rank tells you how many dimensions can be spanned by the output of the linear transformation described by the matrix. If a matrix has a full rank (i.e., rank equals the lesser of the number of rows or columns), it means that all its columns contribute uniquely to the image.
Examples & Analogies
Think of rank like the number of paths leading out of a park: if there are multiple unique paths (let’s say 5) that connect the park to the surrounding areas, the park’s 'rank' is 5. Each path allows you to reach a new destination, similar to how each independent column adds dimension to the output of the matrix.
Understanding Nullity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Nullity ≡ dim(Null space of A)
Detailed Explanation
Nullity represents the dimension of the null space of the matrix A. The null space consists of all the solutions x that satisfy the equation Ax=0. The nullity indicates how many degrees of freedom exist in the solution to this homogeneous equation. Essentially, the greater the nullity, the more solutions exist, but they must all lie within the constraints set by the original equations represented by the matrix.
Examples & Analogies
Imagine a job with specific requirements (the parameters set by the matrix). Nullity represents the number of ways you can fill a position without meeting one of those requirements. For instance, if a job requires a degree or extensive experience, and the nullity is high, there may be many candidates who don’t meet every requirement but could still be considered for the job based on their unique qualifications or skills.
Implications of the Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This provides insight into the dimension of the solution space of Ax=0.
Detailed Explanation
The Rank-Nullity Theorem not only provides an arithmetic relationship among rank, nullity, and the number of columns, but it also offers significant information about the solution space for the system of equations represented by Ax=0. If the nullity is greater than zero, it indicates that there are infinitely many solutions to this equation, while a nullity of zero means the only solution is the trivial solution (x=0). By understanding this, one can determine the nature of solutions present in a system and thus analyze its behavior more effectively.
Examples & Analogies
Think of a classroom where students are assigned to work on projects (the equations). If all groups have a unique approach (high rank) and no groups have overlapping ideas (nullity is zero), their projects will be independent. However, if several groups are based on the same idea while having some unique elements (indicative of non-trivial solutions), then you’ll have multiple ways of completing the project, demonstrating how nullity gives insight into various approaches to problem-solving.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Rank: The number of linearly independent rows or columns in a matrix.
-
Nullity: The number of free variables in the solution to Ax=0, representing dimensions where solutions can exist.
-
Rank-Nullity Theorem: A pivotal relationship stating that Rank(A) + Nullity(A) = number of columns.
-
Column Space: The subspace formed by all linear combinations of the matrix's columns.
-
Null Space: The solution space for the equation Ax=0, indicating possible solutions to the system.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: For a matrix A of size 4x3, if Rank(A) = 2, then Nullity(A) = 3 - 2 = 1, indicating that there is one free variable in the system Ax=0.
-
Example 2: In a real-world context, an engineering problem may involve multiple designs with certain constraints. By analyzing the rank and nullity of the design matrix, engineers can identify flexible design options or pinpoint the design failures.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Rank and Nullity, one is free, their sum gives columns, in harmony.
📖 Fascinating Stories
-
Imagine a library where each book (column) has readers (rank); if some books read by no one (nullity), we still count all books (columns) in our library tally.
🧠 Other Memory Gems
-
R+N=C: Rank plus Nullity equals Columns – RNC for Rank, Nullity, Columns!
🎯 Super Acronyms
RNC
- Remember
- Nullity counts the free
- Rank shows independence
- together they define!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rank
Definition:
The dimension of the column space of a matrix, indicating the number of linearly independent columns.
-
Term: Nullity
Definition:
The dimension of the null space of a matrix, representing the number of solutions to the homogeneous equation Ax = 0.
-
Term: Column Space
Definition:
The subspace formed by the linear combinations of the columns of the matrix.
-
Term: Null Space
Definition:
The subspace formed by the solutions to the equation Ax = 0.
-
Term: Image
Definition:
The set of all possible output vectors produced by a matrix when applied to input vectors.