Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Overdetermined Systems
Unlock Audio Lesson
Today, we are going to discuss overdetermined systems. Can anyone tell me what we mean by 'overdetermined'?
Is it when there are more equations than unknowns?
Exactly! When we have more equations than variables, this usually means we might not be able to find an exact solution. What do you think we would want to do in such cases?
Maybe we try to minimize the differences somehow?
Yes! We aim to minimize the error in a least squares sense. This means we want to find a solution that gets us as close as possible to satisfying all our equations. Can anyone think of a practical example where this might be important?
Curve fitting?
Correct! Curve fitting is a perfect application. Let's summarize what we've learned: Overdetermined systems have more equations than unknowns and we use least squares methods to find an approximate solution.
Mathematical Representation of Overdetermined Systems
Unlock Audio Lesson
Now, let's look at the mathematical representation. We minimize the expression by finding a solution vector x that minimizes the difference between Ax and b. Can anyone recall how we express this mathematically?
It's something like min ||Ax - b||²?
That's right! And from this, we derive the normal equations. What do those equations look like?
I think it’s A^TAx = A^Tb?
Perfect! This set of equations gives us the best approximation of x for our system. Remember, this is essential in applications like sensor network calibrations. To sum up, overdetermined systems lead us to use the least squares method and derive normal equations for solutions.
Applications of Overdetermined Systems
Unlock Audio Lesson
Let's explore some real-world applications of overdetermined systems. Where can we see least squares approximations being employed?
In civil surveying!
Exactly! It helps in determining the best estimate for land measurements. Any other examples?
What about curve fitting for experimental data?
Correct again! It's also used in sensor network calibration. When we have inaccurate data points, we can still find a useful estimate for the underlying function. So remember, overdetermined systems guide us in precise modeling across various fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In overdetermined systems, represented by more equations than unknowns (m > n), solutions may not exist. Instead, a least squares approach aims to minimize the error between the estimated and actual solutions. The resulting solution is calculated using the normal equations from the pseudo-inverse method, particularly useful in practical applications like civil surveying and curve fitting.
Detailed
Overdetermined Systems
Overdetermined systems occur when there are more equations than unknowns, represented mathematically as m > n, where 'm' is the number of equations and 'n' is the number of unknowns. These systems may often be inconsistent, meaning there may not be an exact solution that satisfies all equations simultaneously. The objective in such cases is usually to find a solution that minimizes the error in a least squares sense.
To achieve this, we focus on minimizing the distance (or norm) between the actual output vector b and the predicted output vector Ax. This minimization leads to the formulation:
$$\text{min} ||Ax - b||_2^2$$
Consequently, the solution is derived from the normal equations formulated as follows:
$$A^TAx = A^Tb$$
This form helps in finding the best approximation to the solution, especially in scenarios like civil surveying, where accurate positional data is essential. Additionally, this method is fundamental in curve fitting processes and sensor network calibrations, making it crucial in engineering and applied mathematics.
Youtube Videos
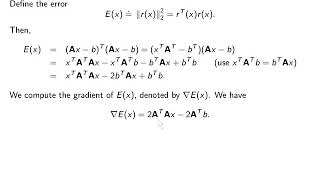
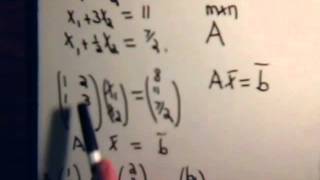
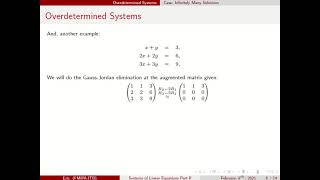
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Overdetermined Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When m > n, the system may be inconsistent. In such cases, we seek a solution that minimizes the error in a least squares sense: min∥Ax−b∥².
Detailed Explanation
An overdetermined system occurs when there are more equations (m) than unknowns (n). This situation often leads to inconsistencies, meaning that the equations may not all be satisfied at the same time. To address this, we find a solution that minimizes the difference between the left side (Ax) and the right side (b) in a least squares manner. The expression min∥Ax−b∥² defines this minimization, where ∥Ax−b∥ represents the Euclidean norm of the vector difference between Ax and b.
Examples & Analogies
Imagine you are trying to fit a straight line to a set of points on a graph (like in a linear regression). If you have more points than the dimensions of the line (which is 2D, with a slope and an intercept), you may find that no single line can pass through all points simultaneously. Instead, the best approach is to find a line that minimizes the total distance from all the points, which is what least squares fitting achieves.
Mathematical Formulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The solution is given by: AT Ax=ATb.
Detailed Explanation
To find the least squares solution to an overdetermined system represented by Ax = b, we reformulate the problem in terms of matrix operations. The equation AT Ax = ATb arises from setting the derivative of the error term with respect to x to zero. Here, AT is the transpose of matrix A, and the left side (AT A)x represents transforming the problem into a system that can accurately approximate the solution for x. This adjustment enables us to solve for the best fit in a consistent manner.
Examples & Analogies
Think of this as trying to find the optimal angle to shoot a basketball to make the most successful baskets. You have several attempts (each being an equation), but varying factors such as your position and the wind (more complex than a simple shot) affect the outcome. By creating a 'best fit' model, similar to the equation AT Ax = ATb, you can find the angle that minimizes your missed shots, leading to a more effective shooting strategy.
Applications of Overdetermined Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Used in:
- Civil surveying.
- Curve fitting in construction data.
- Sensor network calibration.
Detailed Explanation
Overdetermined systems are pivotal in various fields, particularly when multiple measurements or equations are available to solve for a limited number of unknowns. In civil surveying, for example, multiple data points from different locations are used to determine the best fit for land contours or structure placements. Similarly, in curve fitting, data collected from experiments can lead to the optimal mathematical model representing the underlying phenomena. Sensor networks often generate data that needs to be calibrated accurately, ensuring the readings are correct despite potential inconsistencies in the measurements.
Examples & Analogies
Consider the process of strain gauge measurements on a bridge. Different sensors spread across the structure collect data on how the bridge behaves under weight. These readings can be inconsistent due to noise or inaccuracies. By utilizing an overdetermined system approach, engineers apply least squares to find a single model that best represents all sensor data, ensuring the accuracy of their assessments regarding the bridge's structural integrity.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Overdetermined System: A system with more equations than unknowns, often leading to inconsistencies.
-
Least Squares Approximation: A technique used to minimize the error in overdetermined systems.
-
Normal Equations: Generated from least squares methods to find the best fit solution.
-
Pseudo-Inverse: A mathematical tool to solve certain systems that are not invertible.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In civil engineering, least squares methods are employed in surveying to obtain accurate land measurements.
-
Curve fitting in statistical analysis often utilizes overdetermined systems to approximate relationships.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Equations abound, more than the unknown, seeking the closest answer to what is shown.
📖 Fascinating Stories
-
Imagine a detective with too many clues for one case, trying to fit them all together but often requiring the best guess instead of a complete solution.
🧠 Other Memory Gems
-
Remember 'Least Squares' = Leaning towards accuracy over exactness.
🎯 Super Acronyms
A.F.I.N.E. - Approximate Fit In Overdetermined Equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Overdetermined System
Definition:
A system of equations with more equations than unknowns, often leading to no exact solution.
-
Term: Least Squares Approximation
Definition:
A method to find the best fit solution by minimizing the sum of the squares of the differences between observed and calculated values.
-
Term: Normal Equations
Definition:
Equations derived from least squares approximation, typically expressed as A^TAx = A^Tb.
-
Term: PseudoInverse
Definition:
A generalization of the inverse matrix used in solving systems that are not square or not invertible.