Introduction to System Responses
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
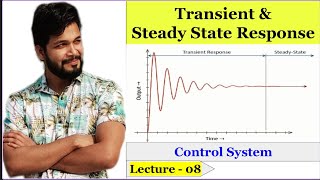
Transient Response
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss the transient response of control systems. Can anyone tell me what we mean by transient response?

Is it how the system reacts to a sudden change, like a step input?

Exactly! The transient response is how a system behaves right after an input change. It's measured by characteristics like rise time, overshoot, and settling time. Does anyone remember what rise time represents?

I think rise time is the time it takes for the output to go from 10% to 90% of its final value.

Correct! Remember that rise time indicates how quickly the system responds to changes. Let's also discuss overshoot. Can anyone define it?

Overshoot is the maximum peak of the output response compared to the steady-state value.

Great! Too much overshoot can affect system performance. Let’s summarize — transient response involves rise time, settling time, overshoot, and peak time.
Steady-State Response
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's pivot to steady-state response. What do you think this refers to?

Is it about how the system behaves after everything has settled?

Exactly! The steady-state response shows how the output behaves with a constant input, after transient effects die down. What do we call the difference between desired and actual output in this state?

That's the steady-state error!

Correct! We determine steady-state error using error constants for different inputs. Can anyone give an example of one of these constants?

The position error constant Kp for step inputs.

Spot on! Understanding steady-state responses is essential for assessing a system's accuracy. To summarize, steady-state responses relate to constant inputs, error constants, and steady-state error.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Understanding system responses is vital for control system design. This section outlines the differences between transient and steady-state responses, explaining how each phase impacts system stability, speed, and accuracy.
Detailed
Detailed Summary of Introduction to System Responses
In control systems, a thorough understanding of system responses is crucial for designing stable and high-performance systems. System responses are classified into two main phases:
- Transient Response: This refers to the system's immediate reaction following a change in input, such as a step input. It is concerned with how the system behaves initially after disturbances and how quickly it approaches its ultimate value.
- Steady-State Response: This phase reflects the long-term behavior of the system after it has settled and reached equilibrium. It helps understand the system's behavior once transient effects have diminished.
Both responses are integral to evaluating the speed, stability, and accuracy of control systems. Designers must assess them to ensure optimal performance in various operational conditions.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Importance of Understanding System Responses
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In control systems, understanding the system response is essential to designing stable and high-performance systems.
Detailed Explanation
To engineer effective control systems, it's crucial to understand how these systems respond to different inputs. This understanding helps design systems that maintain stability and perform well under various conditions.
Examples & Analogies
Think of a car's steering system; when you turn the wheel, the car needs to respond smoothly and predictably. If the steering system isn't designed well, the car could swerve or respond too slowly, making it difficult and potentially dangerous to drive.
Phases of System Response
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A system's response can be divided into two primary phases:
1. Transient Response: The behavior of the system immediately after a change in input (such as a step input) before it reaches steady-state. It reflects how the system reacts to initial disturbances and how quickly it settles to its final value.
2. Steady-State Response: The behavior of the system after it has had enough time to settle and reach equilibrium. It reflects how the system behaves once transient effects have subsided.
Detailed Explanation
System response is categorized into two distinct phases. The transient response captures the system's immediate reaction to changes, while the steady-state response indicates the system's long-term behavior after settling down. Both phases are significant for evaluating how effectively a control system operates.
Examples & Analogies
Consider boiling water. Initially, when you turn on the heat (the input change), there’s a quick reaction (transient response) as the water heats up and starts bubbling. Eventually, when the water reaches a steady temperature (steady-state response), it maintains that temperature until you turn the heat off.
Significance of Both Responses
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Both responses are important for assessing system stability, speed, and accuracy.
Detailed Explanation
Analyzing both the transient and steady-state responses helps engineers ensure that a system behaves predictably and efficiently. A stable system quickly settles to a desired value without excessive oscillations or delay. Understanding these responses allows designers to fine-tune systems for optimal performance.
Examples & Analogies
In a roller coaster, the initial drop creates excitement (transient response) but if the ride ends smoothly and safely (steady-state response), it reassures passengers that the ride was well-designed. Engineers need to focus on both aspects to provide a thrilling yet safe experience.
Key Concepts
-
Transient Response: Behavior of a system immediately after an input change.
-
Steady-State Response: The system's behavior in equilibrium after transients.
-
Error Constants: Quantities used to compute steady-state error for different input types.
Examples & Applications
In a car's acceleration from a stop, the initial quick surge represents the transient response, while the car maintaining a constant speed is the steady-state response.
For a step input in an electrical circuit, observing how the voltage rises quickly and then stabilizes illustrates the transient and steady-state responses.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Settling tight, just hold on tight; Transient reacts, steady's in sight.
Stories
Imagine a runner (transient) bursting out of the starting line but eventually finds their pace (steady-state).
Memory Tools
Remember the acronym ROSS: Rise, Overshoot, Settle, Steady-state for transient response.
Acronyms
SORE - Steady, Overshoot, Rise, Equilibrium.
Flash Cards
Glossary
- Transient Response
The immediate response of a system following a change in input, showcasing how quickly it approaches a steady state.
- SteadyState Response
The behavior of a system when it has settled into a constant state, reflecting its performance following transient effects.
- Rise Time (trt_r)
The duration it takes for the output to move from 10% to 90% of its final value.
- Settling Time (tst_s)
The time needed for the output to remain within a certain percentage of its final value.
- Overshoot (MpM_p)
The extent to which the output exceeds its final steady-state value, typically expressed as a percentage.
- Damping Ratio (ζ)
A dimensionless measure indicating the level of damping in a system, affecting speed and oscillation.
- Natural Frequency (ωn)
The frequency at which a system oscillates in the absence of damping, significant for transient response.
- SteadyState Error
The difference between the expected output of a system and its actual output as time approaches infinity.
- Error Constants
Quantities that help to determine the steady-state errors for different types of input, such as step, ramp, and parabolic.
Reference links
Supplementary resources to enhance your learning experience.
