Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Combinational Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are exploring combinational circuits, which are circuits where the output is solely based on the current inputs. Can anyone describe what we mean by 'current inputs'?
I think it means the inputs that are happening right now, without considering anything from before.
Exactly! Current inputs are the signals processed at the moment, and the circuit outputs depend only on these signals. Let's use the acronym 'CIRCLES'βCurrent Inputs Result in a Combination of Logic Elements. Can you all remember that?
That makes sense! So, these circuits donβt remember anything?
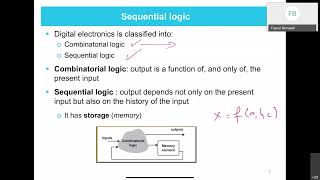
Correct! They do not have memory. Unlike sequential circuits, which can store previous states, combinational circuits work instantly.
What about the types of combinational circuits? Are there examples?
Great question! Yes, examples include adders, multiplexers, decoders, and comparators. Each serves different purposes. Let's summarize: Combinational circuits handle current inputs only; examples include adders and logic gates.
Types of Combinational Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand what a combinational circuit is, letβs discuss specific types. Starting with adders, can someone explain what an adder does?
An adder adds two binary numbers together.
Exactly! Thereβs the half adder for simple addition of two bits and a full adder which can take in a carry bit as well. Can anyone tell me the difference?
A half adder doesnβt take a carry in, but a full adder does!
Correct! Remember, 'HALF has no Carry'βuse that mnemonic to differentiate. Now, shifting gears, what is a multiplexer?
It selects one input from multiple inputs based on control signals.
Well done! Multiplexers are like traffic managers for data in the circuit. So, to summarize: half adders and multiplexers are key combinational circuits, each with distinct roles.
Applications of Combinational Circuits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs take a moment to explore why understanding these circuits is essential. Can anyone think of a real-life application of combinational circuits?
Digital calculators use adders to perform math operations.
Right! Calculators are a perfect example. Combinational circuits are also critical for computer processors and signal routing. How do you think they make our devices faster?
Because they process information quickly without waiting on previous input states?
Exactly! Their ability to provide instantaneous outputs contributes to overall efficiency. Letβs wrap this up: Combinational circuits are vital in various applications, such as calculators and data multiplexing, emphasizing their importance in digital circuit design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into combinational circuits, which compute their outputs based only on present inputs through Boolean operations. It outlines characteristic examples, emphasizing their distinction from sequential circuits, which consider previous states.
Detailed
Understanding Combinational Circuits
Combinational circuits are a foundational concept in digital design, emphasizing that the output is determined exclusively by the current set of inputs. Unlike sequential circuits, combinational circuits lack memory; hence, they do not retain information about prior states.
The circuits operate through Boolean algebra, employing basic logic gates and facilitating essential functionalities. Common examples of combinational circuits include:
- Adders (such as Half Adders and Full Adders)
- Multiplexers (MUX) which select one of several input signals
- Decoders that translate binary information from coded inputs into unique outputs
- Encoders performing the opposite function of decoders
- Comparators that compare two values and provide output based on their equality or inequality
- Basic Logic Gates (AND, OR, NOT, XOR).
The understanding of combinational circuits is crucial for designing complex digital systems, as they form the basis for more complex sequential logic circuits.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Combinational Circuits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Combinational circuits are circuits where the output is purely a function of the present input. The output is determined by applying Boolean operations to the inputs. These circuits do not have memory or storage capabilities and respond instantly to changes in input.
Detailed Explanation
Combinational circuits are a fundamental type of digital circuit where the output is directly determined by the current inputs. This means that if you change the input, the output will change instantaneously based on predefined Boolean logic (e.g., AND, OR, NOT). Unlike sequential circuits, they do not remember past states or inputs; their response is solely based on what they are currently receiving.
Examples & Analogies
Think of a light switch in your home. When you flip the switch (input), the light (output) turns on or off immediately, without retaining any memory of the previous state. If you flip the switch again, the light responds right away based on the new input.
Basic Examples of Combinational Circuits
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Basic Examples of Combinational Circuits:
β Adders (e.g., half adder, full adder)
β Multiplexers (MUX)
β Decoders
β Encoders
β Comparators
β Logic Gates (AND, OR, NOT, XOR)
Detailed Explanation
Combinational circuits can take various forms, each serving a different purpose in digital logic design. Some common types include:
- Adders: Circuits used for addition (such as half adders and full adders).
- Multiplexers (MUX): Select one of many inputs to pass through to the output.
- Decoders: Convert binary information from n input lines to a maximum of 2^n unique output lines.
- Encoders: Perform the reverse of a decoder, taking multiple input lines and encoding them into a fewer number of output lines.
- Comparators: Used to compare two binary values.
- Logic Gates: Basic building blocks like AND, OR, NOT that perform logical operations on one or more binary inputs.
Examples & Analogies
Consider a vending machine for the examples: it can be viewed as a combinational circuit, where the coins you insert (the inputs) determine whether you get your desired snack (the output). Different combinations of coins (inputs) either result in the machine giving you a snack or returning your coins based on defined rules, similar to how logical operations dictate the outputs in combinational circuits.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Current Inputs: Signals present at any moment in time that determine the output.
-
No Memory: Combinational circuits do not retain past information.
-
Boolean Operations: Fundamental mathematical operations used to derive outputs from inputs.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Half Adder: A simple device that adds two single binary digits and outputs their sum and carry.
-
Full Adder: An adder that can handle a carry input and generate a carry output.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To add bits here and there, full adders handle carry with flair.
π Fascinating Stories
-
Once upon a time, two bits wanted to marry. The full adder brought a carry into their family!
π§ Other Memory Gems
-
Remember 'LOCK' for Logic Operators Creating Knowledge: Logic gates create functions.
π― Super Acronyms
CIRCLE - Current Inputs Result in a Combination of Logic Elements.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Combinational Circuit
Definition:
A digital circuit whose output depends solely on the current inputs.
-
Term: Boolean Operations
Definition:
Mathematical operations based on Boolean algebra, involving true/false values.
-
Term: Adder
Definition:
A circuit that performs the addition of binary numbers.
-
Term: Multiplexer (MUX)
Definition:
A device that selects one of many input signals and forwards it to a single output line.
-
Term: Decoder
Definition:
A circuit that converts binary data from encoded inputs to unique outputs.
-
Term: Encoder
Definition:
A circuit that converts information from one format to another, typically from analog to digital.
-
Term: Comparator
Definition:
A device that compares two values and determines their equality or inequality.