Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to FSMs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about Finite State Machines, or FSMs. Can anyone tell me what they think an FSM is?
Is it a method to keep track of what a system is doing at any moment?
Exactly! FSMs model systems that can exist in a finite number of states. They help us understand and design complex systems by breaking them down into manageable parts. Can anyone give me an example of where we might use an FSM?
Like in a traffic light system?
Yes, that's a perfect example! In a traffic light system, each light represents a different state of the FSM. Now, let's remember this with the acronym 'TEA'βTransitions, Events, and Actions. These are crucial in how FSMs function.
So the traffic light changes based on events like cars approaching?
Exactly! Great connection. Letβs summarize: FSMs are crucial for modeling systems because they only allow a finite number of states and transitions based on inputs.
Components of FSMs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Alright, letβs dive deeper into FSMs. Can someone explain what the main components of an FSM are?
States and transitions?
Correct! States are the various conditions that an FSM can be in, and transitions are the rules for moving from one state to another. Why do you think that this distinction is important?
It helps us understand system behavior and how it reacts to inputs.
Right! The clarity provided by states and transitions allows for systematic design and analysis. Letβs remember 'S-TAP'βStates, Transitions, Actions, and Processes. This helps us keep the essential elements of FSMs in mind.
What about the outputs? Are they linked to states?
Good point! Outputs in FSMs are indeed correlated with the current states. Letβs summarize: FSMs consist of states and transitions, providing a robust model for analyzing dynamic systems.
Real-world Applications of FSMs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand FSMs, letβs talk about where we see them in real life. Can anyone mention an application?
Digital clocks!
Exactly! Digital clocks cycle through states based on time increments. Who can think of another example?
How about video game states, like moving from the menu to the game?
Great! Video games often utilize FSMs to manage different states of gameplay. Letβs use the mnemonic 'TRAC' for Traffic systems, Real-time systems, Applications in gaming, and Control systems, to remember the examples of FSMs.
So, FSMs are everywhere! Thatβs interesting!
Exactly! They are integral to modern system designs. To recap, FSMs can be applied broadly from traffic lights to digital controllers because they help simplify state management effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
FSMs are a fundamental design element in digital systems that can represent states and transitions based on inputs. They are essential in applications like traffic light controllers, digital clocks, and more, allowing systems to behave predictively based on current and past input states.
Detailed
Understanding FSMs
Finite State Machines (FSMs) are an essential concept in digital system design, particularly in control applications where a system can exist in a finite number of states. FSMs are instrumental in various technical domains including traffic light control systems, control systems, digital clocks, and protocol handlers. The basic principle of FSMs is that they transition between a limited number of predetermined states based on input signals and can output different actions based on the current state.
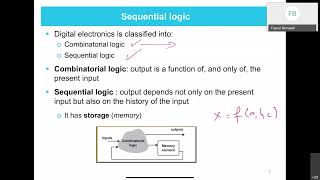
FSMs are comprised of two primary elements: states and transitions. States represent the various conditions or configurations at any given moment, while transitions dictate how the FSM progresses from one state to another in response to input signals. Typically, FSM designs involve the use of flip-flops for state memory and combinational logic to govern state transitions and outputs.
In system design, FSMs simplify the design process while providing a clear representation of behavior, enhancing both debugging and system integrity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to FSMs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
FSMs are used to model systems that have a finite number of states.
Detailed Explanation
FSMs, or Finite State Machines, are a type of computational model used in designing logic systems or controllers. They are characterized by a finite number of statesβthe conditions or statuses that the system can be in at any given time. Transitioning from one state to another is dictated by specific input signals.
Examples & Analogies
Think of a traffic light. It can be in one of three states: Red, Yellow, or Green. Depending on the current state and certain inputs (like a timer), it will switch to the next state. This model helps us understand how the traffic light functions predictably and ensures the traffic flows smoothly.
Applications of FSMs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
They are widely used in control systems, digital clocks, traffic light controllers, and protocol handlers.
Detailed Explanation
FSMs are utilized in various applications where predefined conditions must dictate system behavior. For instance, in a digital clock, the state could represent the time in hours and minutes, transitioning with each clock tick. Similarly, traffic light controllers rely on FSMs to determine the sequence and duration of light changes to maintain safe traffic flow.
Examples & Analogies
Consider a simple vending machine. It uses an FSM to manage states like selecting a product, checking if the correct amount of money is inserted, and dispensing the product. Each state has specific transitions based on user actions, ensuring a functional and orderly process.
Implementation of FSMs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
FSMs are typically implemented using flip-flops and combinational logic to define the state transitions and outputs.
Detailed Explanation
In designing FSMs, flip-flops are used as memory elements to store the current state of the machine, while combinational logic circuits determine the conditions under which the transitions between states occur. This ensures a clear mapping from inputs to state changes and subsequent outputs.
Examples & Analogies
Imagine the gears in a simple clock mechanism. The flip-flops act like the gears that keep track of the current time state, while the combinational logic is akin to a set of rules guiding their interactions to ensure the clock ticks smoothly from one time to the next without skipping.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Finite State Machines (FSM): A model that represents systems with a finite number of states.
-
States: Specific configurations within an FSM.
-
Transitions: Rules dictating the movement between states.
-
Outputs: Results derived from current states and inputs.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A traffic light controller that changes the light based on time intervals, cycling through red, yellow, and green states.
-
A digital clock that transitions between hours and minutes based on user interactions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
FSMs have states that do change, with events that keep them in range.
π Fascinating Stories
-
Imagine a traffic light that always knows when to shift from red to green safely focusing on time and cars.
π§ Other Memory Gems
-
Remember TEA: Transitions, Events, Actions when thinking of FSMs.
π― Super Acronyms
S-TAP
- States
- Transitions
- Actions
- Processes for understanding FSMs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Finite State Machine (FSM)
Definition:
A computational model that represents a system with a finite number of states and transitions between those states based on inputs.
-
Term: State
Definition:
A specific condition or configuration that an FSM can be in at any given time.
-
Term: Transition
Definition:
The movement from one state to another in an FSM, which is triggered by an event or input.
-
Term: Output
Definition:
The result produced by the FSM based on its current state and inputs.