Deformations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Translations in Fluid Elements
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss how fluid elements translate from one point to another. Can anyone tell me what we mean by translations in fluids?

Isn’t that when a fluid particle moves from point A to point B?

Exactly! The movement is defined by the velocity components, u, v, and w in the x, y, and z directions respectively. The displacement can be calculated using the formula: Displacement = Velocity × time. Can anyone provide an example of this?

If water is flowing through a pipe, we can calculate how far a particle moves from the inlet to the outlet during a certain time.

Great example! Remember, the translations depend on the flow's velocity profile. To summarize, translations are about understanding how fluid particles travel through a flow field induced by their velocity.
Rotations and Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s shift our focus to rotational motions within fluids, specifically vorticity. Who can explain what vorticity is?

Isn't it the measure of rotation of fluid particles?

Exactly! Vorticity can be mathematically defined as the curl of the velocity field. It quantifies how much a fluid element is rotating in space. If we consider angular velocity, what factors do you think impact it?

I think it would depend on the velocity variation between different points in the fluid.

Absolutely! This relationship is key to understanding fluid dynamics, especially in situations involving turbulence. To sum up, vorticity helps us understand the rotational movements of fluid particles in motion.
Strain Rates in Fluids
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into strain rates now. What do you understand about linear strain in fluids?

It relates to how a fluid element stretches or compresses when stress is applied, right?

Correct! Linear strain is the rate of change in length per unit length. And how does shear strain play a role here?

Shear strain involves the change in shape without volume change, like in fluids flowing through constrictions.

Excellent point! Understanding these strains helps us analyze stresses experienced by fluid elements. In summary, both linear and shear strains are fundamental in characterizing how fluids deform.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we delve into fluid deformations, discussing the motions of fluid elements under various conditions, including translations and rotations and how these movements relate to strain rates. Key concepts include vorticity, linear deformation, shear strain, and the significance of velocity gradients in fluid mechanics.
Detailed
Detailed Summary of Deformations
This section of the chapter on Fluid Mechanics focuses on the concept of deformations within fluid motion. Fluid elements can undergo changes in shape and position, influenced by the fluid's motion represented through translations and rotations. These deformations can be characterized by various types of strain rates including:
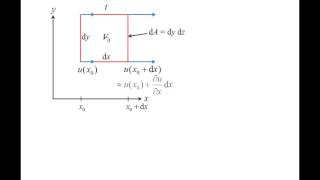
- Translations: The displacement of fluid elements is driven by the velocity components in the x, y, and z directions, resulting in a relative movement from point A to B based on the scalar velocity components.
- Rotations: Angles of rotation (angular velocity) are introduced as a result of velocity variations across a fluid element. The rotations can be computed through the relative differences between velocity components at different points, leading to the concept of vorticity, which quantifies the rotation of fluid particles.
- Strain Rates: Two important types of strain rates are Linear and Shear. Linear strain captures the rate of elongation/shortening of a fluid element, while shear strain measures how a fluid element distorts due to applied stresses.
- Vorticity: Vorticity represents the rotational aspect and is described mathematically as the curl of the velocity vector field. Understanding vorticity is essential for describing fluid behaviors, especially in turbulent flows.
The application of these concepts is crucial in fields such as aerodynamics, hydrodynamics, and any scenario where fluid motion is present. The interplay between velocity gradients and resulting deformations is fundamental in analyzing fluid behavior under various conditions.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Element Motions
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you come back to our basic fluid mechanics okay, so as in the last class I talked about 2 types of descriptions; one is Eulerian frame of descriptions, another is Lagrangian frame of description and that the descriptions we try to visualize as form of virtual fluid balls, okay. So, today I will talk about that I have the fluid element which is you know in any of fluid mechanics book. They talk about the fluid element which is representing a certain space of the fluid particles which is much larger scale than the molecules levels or it is not that bigger scale to represent the flow process.
Detailed Explanation
In fluid mechanics, we can understand fluid behavior using two distinct frames of reference: Eulerian and Lagrangian. The Eulerian approach focuses on specific locations in space, observing how fluids flow past these points over time. Conversely, the Lagrangian perspective tracks individual 'fluid elements' or 'virtual fluid balls' as they move through the fluid. This means that instead of just looking at motion at one point, we can visualize the movement and transformations of these elements as they interact with their surroundings. You can think of these virtual fluid balls as being larger than individual molecules but smaller than sections of fluid, helping us analyze the fluid's properties effectively.
Examples & Analogies
Imagine you are tracking a ball in a crowded stadium (Lagrangian approach) versus watching the crowd from a fixed spot (Eulerian approach). When you focus on the ball (Lagrangian), you can see its journey and how it interacts with people around it. In contrast, if you're at your fixed spot (Eulerian), you notice the patterns of movement of many people as they flow past your view.
Types of Movements of Fluid Elements
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, when you have balls then it can have go through any type of motions and the differences like it can be translations like variations that you have a ball, it can be translated, it can go in a u direction or v direction. Or it can have a displacement in a x direction, y direction, z direction and if the displacement is caused because of the velocity component...
Detailed Explanation
Fluid elements can undergo two main types of movements: translation and rotation. Translation refers to the movement of the fluid element from one place to another, which can occur in any direction based on the velocity components of the fluid (u, v, w). For example, if a fluid element moves from point A to point B in three-dimensional space, we can calculate its new position based on its velocity at the initial time. Rotation, on the other hand, involves the fluid element spinning around an axis. This rotational motion can be clockwise or counterclockwise and depends on the velocity gradients within the fluid. Understanding these movements helps us analyze how fluids behave in different scenarios.
Examples & Analogies
Think of water in a rotating carousel (rotation) and water flowing from a faucet (translation). As water flows from the faucet, it travels in a predictable path, moving from a higher to a lower point (translation). Meanwhile, the water in the carousel swirls around due to the rotation of the carousel, demonstrating how water can also spin around an axis.
Deformations of Fluid Elements
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
the fluid element can go for a rotation, so that means we can compute what could be this angular velocity, if it is going through a rotation; the clockwise rotations or anti-clockwise rotations. So, if you try to understand that these rotations all depends upon the velocity fields, the velocity of the field also talk about how the translations motion will happen from point A to point B...
Detailed Explanation
When fluid elements rotate, they can experience angular velocity which tells us how fast and in what direction they are rotating. This rotation can be influenced by the velocity distribution around them. Additionally, fluid elements can deform when they are subjected to forces; this can happen in the form of linear strain or shear strain. Linear strain occurs when the fluid element is stretched or compressed, altering its dimensions, while shear strain occurs when adjacent particles slide past each other, changing the shape but not the volume. Understanding these deformations is crucial because it helps us describe fluid behavior under various flow conditions.
Examples & Analogies
Imagine stretching a rubber band (linear strain) or twisting a piece of clay (shear strain). As you stretch the rubber band, it becomes longer; as you twist the clay, its shape changes even though the amount of material stays the same. Similarly, fluid elements experience deformations as they flow, which affects their dynamics in a fluid system.
Key Concepts
-
Translations: Movement of fluid particles from one point to another.
-
Rotations: Angular shifts in fluid elements resulting from velocity variations.
-
Vorticity: A key parameter for quantifying the rotation of fluid, crucial for understanding dynamics.
-
Linear Strain: Rate of change in length of fluid elements.
-
Shear Strain: Change of angle between intersecting lines in a fluid from deformation.
Examples & Applications
Example of water flowing through a pipe demonstrating translations.
Analyzing the rotation of fluid elements in a cyclone using vorticity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a gentle stream, fluids glide, from A to B, they do not hide.
Stories
Imagine a dance of fluid particles, swirling and stretching, sometimes rolling, showing us how they move and deform under different pressures, just like a playful group of children on a merry-go-round.
Memory Tools
To remember strain types: 'Linear means stretch, shear means twists, keep these in mind on your fluid shifts!'
Acronyms
Remember V.S.T.R for Vorticity, Strain, Translation, and Rotation - the essence of fluid motions.
Flash Cards
Glossary
- Translations
The movement of fluid elements from one point to another influenced by velocity components.
- Rotations
The angular movement of fluid particles caused by velocity variations.
- Vorticity
The measure of the local rotation in a fluid, mathematically described as the curl of the velocity field.
- Linear Strain
The rate of change in length per unit length of a fluid element.
- Shear Strain
The rate of change of angle between two perpendicular lines in a fluid element due to deformation.
Reference links
Supplementary resources to enhance your learning experience.
