Vorticity Vectors
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll dive into the concept of vorticity, which quantifies the local spinning motion of fluid particles. Can anyone tell me what they think vorticity might be?

Isn't it related to how fast the fluid is rotating?

Exactly! Vorticity is indeed a measure of the local rotation of a fluid. Now, what do you think affects this rotation?

Could it be the velocity of the fluid?

Great point! The velocity field's curl helps us understand vorticity. Remember, vorticity is mathematically defined as the curl of the velocity vector field.

In essence, it's how the velocity changes over space. A mnemonic to remember this is 'Curl The Wave', referring to the curl operator applied to the velocity vector.

So if there's no change in velocity, there’s no rotation?

Correct! If a fluid element maintains a constant velocity, it won't exhibit any vorticity.

To summarize, vorticity quantifies the rotation of fluid and relies directly on how the velocity field changes. Next, we'll explore how this relates to real-world phenomena.
Vorticity and Angular Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s examine the relationship between vorticity and angular velocity. What do you think this relationship implies?

Does it mean that they affect each other?

Exactly! The vorticity of a fluid is related to twice the angular velocity. This is a crucial concept in understanding the motion of fluid elements. Who can recall what angular velocity is?

Isn't it how fast and in which direction something is rotating?

Right! And it matters significantly in rotational systems when studying fluids. Think of it as the fluid's 'spin rate'.

So, higher vorticity means faster rotations, right?

Exactly! That's why vorticity plays a pivotal role in phenomena such as cyclones. To visualize this, remember: 'Twice to Spin'. Vorticity is double the angular velocity.

In summary, vorticity gives us valuable insights into the rotating behavior of fluids and correlates directly with angular velocity, crucial for many fluid motion analyses.
Applications of Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s connect our understanding of vorticity to real-world applications, especially in cyclone prediction. How do you think understanding vorticity helps in this context?

Maybe it helps to predict where a cyclone is going?

Absolutely! Cyclones behave like large vortices. Understanding how vorticity behaves in these systems is crucial for weather predictions.

Do we have tools to measure this?

Yes, tools like Particle Image Velocimetry help researchers measure fluid velocities and infer vorticity. This data is essential for simulating complex systems like cyclones.

I see how it all connects now!

To wrap up, vorticity is not just theoretical; its practical applications impact areas from weather forecasting to engineering fluid systems. Let’s remember: 'Vorticity is the key to predict the spin of storms and more!'
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Vorticity vectors measure the rotational characteristics of fluid motion, playing a crucial role in fluid dynamics by relating to the velocity field of the fluid. This section also covers the relationship between vorticity and angular velocity, emphasizing the importance of understanding these concepts for real-world applications like cyclone formations.
Detailed
Detailed Summary of Vorticity Vectors
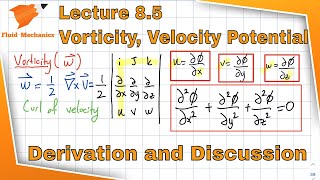
Vorticity, an essential concept in fluid mechanics, pertains to the measure of rotation of fluid elements. It is mathematically expressed in terms of the curl of the velocity field, indicating how velocities change in space.
Key Points Discussed:
- Definition of Vorticity: Vorticity vectors represent the local spinning motion of fluid particles. The mathematical formulation establishes that they can be derived from the velocity field.
- Concept of Angular Velocity: The relation between vorticity and angular velocity is crucial, as the vorticity of a fluid is proportional to twice the angular velocity of the fluid element.
- Importance in Real Applications: Understanding vorticity is vital for analyzing complex fluid behavior in various situations, such as cyclone formation in the Bay of Bengal, where large-scale vortices can influence weather patterns.
- Practical Measurement Techniques: Techniques like Particle Image Velocimetry (PIV) are discussed as effective ways to measure fluid motion and enhance the understanding of turbulence and vortex formation.
- Examples & Applications: Real-world applications and simulations provide context for the theoretical discussions, showcasing how understanding vorticity can help design better fluid systems and predict environmental phenomena.
Youtube Videos
![What you need to know about Vorticity [Fluid Mechanics]](https://img.youtube.com/vi/Xu5IT4bL-v8/mqdefault.jpg)


![Vorticity Explained Conceptually [Aero Fundamentals #67]](https://img.youtube.com/vi/X-hgPslzTcc/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Vorticity
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The vorticity vector, denoted as \( \omega \), is a measure of the rotation of fluid particles. It is mathematically defined as the curl of the velocity vector \( \mathbf{V} \):
$$ \mathbf{\omega} = \nabla \times \mathbf{V} $$
This shows that vorticity represents the angular velocity of fluid motion, where a higher vorticity indicates more rotation within the fluid.
Detailed Explanation
Vorticity provides a quantitative measure of how much and how fast fluid particles are twisting or rotating. When we take the 'curl' of the velocity, we're essentially looking at the local rotation at a given point in the fluid. The higher the vorticity, the more swirling motion is present. If the fluid has no rotation, the vorticity would be zero, indicating laminar flow.
Examples & Analogies
Think of vorticity like the spin of a basketball. When a player spins the ball on their finger, that spin is the vorticity of the ball. In water, if you see a whirlpool, the faster it spins (or the higher the vorticity), the stronger the visual representation of how the water is moving in a circular path.
Relationship Between Vorticity and Angular Velocity
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The relationship between vorticity and angular velocity is characterized by:
$$ \mathbf{\omega} = 2 \mathbf{\Omega} $$
Where \( \Omega \) represents the angular velocity vector. Therefore, the vorticity vector is essentially twice the angular velocity of any fluid particle.
Detailed Explanation
In fluid mechanics, vorticity is a crucial concept because it relates to the motion of the fluid. By understanding how vorticity relates to angular velocity, we can analyze the behavior of fluids in motion. For instance, if we know the vorticity of a fluid, we can effectively determine how swiftly and in what manner the fluid particles are rotating.
Examples & Analogies
Imagine the way a figure skater spins. As they pull their arms in, they increase their spin rate, which is similar to how vorticity increases as fluid experiences changes in velocity. The skater’s spin represents the angular velocity, while the overall rotation they produce can be likened to vorticity.
Vorticity and Flow Field Visualization
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity can also be visualized graphically in flows, particularly in the study of turbulence. Regions of high vorticity can be depicted as swirling or rotating structures, which can be crucial in understanding both the dynamics of fluid flow and the physical processes involved in natural phenomena.
Detailed Explanation
Visualizing vorticity helps identify areas in fluid flow where significant rotation occurs. This is particularly useful in various applications such as weather systems, ocean currents, and engineering flows. By examining vorticity maps, scientists and engineers can predict and manage the behavior of fluids more effectively.
Examples & Analogies
Consider a leaf swirling in a pond. The way the water moves around the submerged leaf shows regions of high vorticity—where the water circulates around the leaf. Observing these vortices can help one to visualize the complexities of fluid flow patterns and might also reflect how airplanes experience turbulence or how hurricanes form.
Key Concepts
-
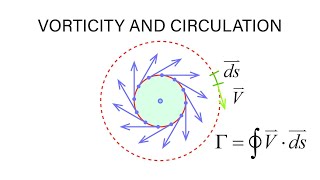
Vorticity: A measure of local fluid rotation affecting flow dynamics.
-
Angular Velocity: Rotational rate of fluid particles crucial for understanding vorticity.
-
Curl: Mathematical operator relating to rotation in fluid motion.
-
Applications: Nurtured understanding of vorticity leads to advancements in forecasting and engineering.
Examples & Applications
Cyclone formation in the Bay of Bengal exemplifies vorticity in natural systems.
Experimental measurement of vorticity using Particle Image Velocimetry (PIV) highlights its practical applications in fluid mechanics.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
'Vorticity spins, like a top in a race, spinning in circles, moving at pace.'
Stories
Imagine a fluid particle like a dancer, twirling around while the world flows past, this is how vorticity describes their graceful rotations.
Memory Tools
Remember 'V.A.C.' - Vorticity, Angular velocity, Curl - to recall these related concepts.
Acronyms
Use 'V.E.C.' for Vorticity Equals Curl
an essential relationship.
Flash Cards
Glossary
- Vorticity
A measure of the rotation of fluid particles in a fluid flow.
- Angular Velocity
The rate of rotation around an axis, often represented in radians per second.
- Curl
A vector operator that describes the rotation of a field in three-dimensional space.
- Particle Image Velocimetry (PIV)
An optical method of flow visualization that enables the measurement of velocity fields in fluid flows.
- Vortex
A flow pattern where fluid moves in a circular motion around an axis.
Reference links
Supplementary resources to enhance your learning experience.
