Velocity Gradients and Rotations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Gradients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we are going to introduce velocity gradients. Can anyone tell me what a velocity gradient is?

Is it how fast the velocity changes with respect to distance?

Exactly! The velocity gradient measures the change in velocity across a distance. It is critical for understanding how fluids move.

How does that relate to fluid rotation?

Great question! As we have changes in velocity, it creates shear, leading to rotations of fluid elements. Remember, the more changes in velocity, the more significant the potential for rotation. This can be summarized as 'VG = V Δx' where VG stands for velocity gradient.
Understanding Rotational Motion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's dive into rotations. Can someone explain what angular velocity means?

Is it the rate at which an object rotates around an axis?

Correct! Angular velocity refers to how quickly a fluid element rotates around a point. It's expressed in radians per second.

So, if the fluid has a higher angular velocity, does that mean it spins faster?

Yes! As angular velocity increases, the rotational effect on the fluid element intensifies. Let's remember this with the mnemonic 'Fast Rotates, Faster Viscous!'
Deformation of Fluid Elements
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Apart from rotation, fluid elements also deform. What types of deformation do you think occur?

Linear and shear strains?

Precisely! Linear strains happen when the length of the fluid element changes, while shear strain occurs when the angles between layers of fluid change.

How can we relate this to velocity gradients?

Good insight! The differences in velocity across the fluid elements influence how these deformations occur. We can summarize this by the phrase 'Different Shifts, Different Shapes'.
Vorticity and Its Implications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s talk about vorticity. Who can explain what it measures in fluids?

Vorticity measures the local rotation of the fluid elements?

Exactly! It’s defined mathematically as the curl of the velocity field. Vorticity is significant because it helps us understand complex flow patterns.

How does it relate to real-world fluids, like cyclones?

Great link! Vorticity plays a critical role in the formation of vortices in weather systems. To remember, think of 'Vorticity = Vortex Power!'
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section delves into the kinematic aspects of fluids, explaining how velocity gradients lead to rotations within fluid elements. It highlights the significance of understanding these concepts in the context of practical applications such as studying vortex formations and fluid deformations.
Detailed
Velocity Gradients and Rotations
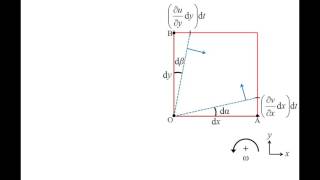
In this section, we explore the concepts of velocity gradients and rotations within fluid mechanics. Fluid kinematics describes the motion of fluids without considering the forces causing the motion. The velocity gradient in a fluid indicates how the velocity of fluid elements changes in space. Understanding these gradients is crucial for analyzing fluid motion, especially in the context of vortex formations and turbulence.
The section introduces the idea of fluid elements, visualized as virtual balls, which can exhibit both translational and rotational motion. Translational motions occur when fluid particles shift from one location to another, while rotations describe the angular movement about an axis. The angular velocity represents the rate of rotation of these fluid elements, which depends on the velocity gradient in the surrounding fluid.
Additionally, the section discusses how fluid elements can undergo deformation, including linear and shear strains, which result from varying velocity fields. The significance of these concepts is illustrated through examples, including real-world applications such as understanding vortex formations in systems like hurricanes and other cyclone phenomena.
Key points covered include:
- The definition and significance of velocity gradients in fluid dynamics.
- The relationships between linear translations and angular rotations of fluid elements.
- The formation of vorticity as a measure of the rotation rate of fluid particles, linked to practical CFD applications.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Motion
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Mixing of water and air is a common occurrence in fluid mechanics. The complexity of fluid dynamics often involves interactions between different fluid domains, such as water and air, leading to intricate flow patterns.
Detailed Explanation
Fluid mechanics involves studying the behavior of fluids (liquids and gases) in motion. One of the key aspects is understanding how different fluids interact with each other. For example, when water flows, it can cause air to mix into it, creating bubbles or turbulence depending on the flow speed. This interaction is vital in various applications, like in aerodynamics and hydraulics.
Examples & Analogies
Imagine pouring a glass of soda that has bubbles. As the soda flows and moves in the glass, the carbon dioxide gas bubbles interact with the liquid, creating a dynamic situation. Just like that, in large water bodies, the interactions between air and water can lead to vortex formations, similar to how whirlpools are formed.
Translation and Rotation of Fluid Elements
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fluid elements can exhibit two types of motions: translations and rotations. Translations occur when fluid particles move from one point to another, while rotations happen around a point within the fluid element.
Detailed Explanation
In fluid mechanics, we consider fluid elements as small volumes of fluid that can translate or rotate. Translation refers to the movement of the entire fluid element from one position to another based on the flow velocity. Rotational motion, on the other hand, is when the fluid element spins around an axis, often due to variations in velocity at different points within the element.
Examples & Analogies
Think of a leaf floating on a pond. As it moves across the water surface (translation), it may also spin around due to currents of water underneath (rotation). This analogy helps to visualize how fluid elements can both move to new locations and rotate simultaneously.
Velocity Gradients and Angular Velocity
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The angular velocity of a fluid element can be described in terms of velocity gradients. These gradients measure how velocity changes over space and time within the fluid.
Detailed Explanation
Angular velocity refers to the rate at which an object rotates around a defined point or axis. In fluids, this can be determined by examining the velocity gradients between different points in the flow. When the velocity changes along the flow path, it leads to rotation of the fluid element—this is where the concept of angular velocity comes into play as a measure of that rotational effect.
Examples & Analogies
Picture a spinning record player. The speed of the record affects how quickly the needle moves across the vinyl. In fluids, when different sections of water flow at different speeds (like our needle on the record), it can create swirling motions, much like how the needle moves constantly due to the change in speed across the record.
Linear and Shear Strain Rates
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Linear strain rates describe the rate of change in length of a fluid element while shear strain rates indicate the change in angle between two lines within the fluid element.
Detailed Explanation
Strain rates are critical in understanding how fluids deform under stress. Linear strain rate measures how much a fluid element stretches or compresses over time, typically when subjected to flow changes. Shear strain rates, on the other hand, show how the angles between lines within the fluid element change, reflecting how the shape deforms due to the fluid's internal stresses.
Examples & Analogies
Consider stretching a rubber band. If you pull both ends, the band elongates—this is similar to linear strain. Now imagine twisting the ends of the rubber band while keeping the center fixed—this creates shear strain. Both actions illustrate how fluids can change shape based on external forces.
Vorticity and Rotationality of Fluids
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity is defined as the measure of the local rotation of a fluid particle and is mathematically represented as the curl of the velocity field.
Detailed Explanation
Vorticity is a fundamental property in fluid dynamics that quantifies the rotational motion of fluid particles. When we calculate the curl of the velocity field, we derive the vorticity vector, which gives a clear picture of how much and in what manner the fluid is rotating. A higher vorticity indicates more intense rotations, commonly seen in swirling fluids like whirlpools or tornadoes.
Examples & Analogies
Imagine a whirlpool in a bath. The water spirals and spins as it drains, creating a visible rotation. This rotation is described by the vorticity of the water. The stronger the drain, the faster the rotation, which graphically represents the concept of vorticity in a body of fluid.
Key Concepts
-
Velocity Gradient: Indicates the rate of change of fluid velocity with distance.
-
Angular Velocity: Refers to how fast a fluid element rotates around a point.
-
Vorticity: A measure of the local rotation of fluid elements in the flow field.
-
Deformation: Change in shape or size of fluid elements due to velocity gradients.
Examples & Applications
In a river, the velocity of water is fastest at the surface and slows down near the bottom due to the velocity gradient.
In a cyclone, the rapid rotation of air creates vortices that cause severe weather patterns.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When fluids flow and speed they shift, the gradient shows the strain they'll lift.
Stories
Imagine a river where the water flows fast at the surface and slow at the bottom, creating vortices—a perfect demonstration of velocity gradients and rotations.
Memory Tools
VAG - Vortex, Angular velocity, Gradient: Remember these key concepts when discussing fluid dynamics.
Acronyms
VGR - Velocity Gradient Relation
Focus on how velocity changes affect both rotation and deformation.
Flash Cards
Glossary
- Velocity Gradient
A measure of how the velocity of a fluid changes in relation to distance.
- Angular Velocity
The rate at which an object rotates around an axis.
- Vorticity
A measure of the local rotation in a fluid, calculated as the curl of the velocity field.
- Linear Strain
Deformation that results in a change in length of a fluid element.
- Shear Strain
Deformation that occurs when layers of fluid slide past each other, altering angles.
Reference links
Supplementary resources to enhance your learning experience.
