Eulerian and Lagrangian Descriptions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eulerian and Lagrangian Descriptions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to explore two important descriptions of fluid motion: Eulerian and Lagrangian. Who can tell me what they think is the difference between these two approaches?

Is the Eulerian approach focused on specific points in the fluid?

Exactly! The Eulerian perspective observes the fluid at fixed locations, measuring how properties like velocity change over time. What about the Lagrangian approach?

The Lagrangian approach looks at individual fluid particles, right?

Yes! It follows the path of fluid particles as they move. This method is crucial for understanding both small-scale turbulence and the trajectories of particles. Let’s remember it with the acronym LAG - Lagrangian Aims to Guide particles.

So, it’s like two different ways of looking at the same fluid?

Exactly! Both are essential for analyzing fluid dynamics comprehensively. Let’s summarize: Eulerian focuses on positions, while Lagrangian focuses on particles.
Applications of Eulerian and Lagrangian Approaches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've discussed the differences, let's talk about some applications. Why do you think we use the Eulerian approach for large-scale flow phenomena?

Because it’s easier to measure properties at fixed points, right?

Correct! It allows us to assess flow quality and turbulence levels without following every particle. And for situations like vortex formations, how does the Lagrangian description help?

It helps us understand how individual particles interact within the vortex.

Good point! So, when aiming to analyze complicated interactions like turbulence, the Lagrangian approach is most beneficial. Can anyone summarize our approaches?

Eulerian is about fixed points, while Lagrangian follows particles.

Well done! Remember, in fluid dynamics, choosing the right approach is key depending on what you want to analyze.
Velocity Fields and Fluid Deformation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s link our discussions to how these descriptions relate to fluid behavior. How do the descriptions affect the velocity field?

In the Eulerian description, we can see how the velocity varies at different points.

Exactly! That understanding is critical for analyzing flow stability and behavior. And what about the Lagrangian description?

It helps track how each particle's velocity affects the overall motion.

Correct! The movement of individual particles can give insight into larger trends, like fluid deformation during flow. Remember the mnemonic: VEL - Velocity and Elemental Lagrangian!

That's catchy! So, the effects of deformation can be linked back to how we model these particles and fixed points.

Absolutely! Understanding flow mechanics ultimately depends on these fundamental approaches.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the concepts of Eulerian and Lagrangian descriptions are explored in detail, highlighting their respective approaches to studying fluid motion. The importance of these descriptions in describing fluid elements, velocity fields, and the resulting rotations and deformations are also examined.
Detailed
Eulerian and Lagrangian Descriptions
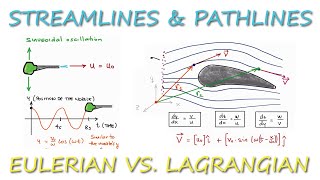
In the realm of fluid mechanics, understanding fluid behavior is crucial for both theoretical studies and practical applications. Two primary approaches exist for describing fluid motion: Eulerian and Lagrangian descriptions.
Eulerian Description
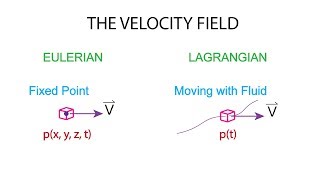
The Eulerian approach focuses on specific locations in the fluid domain, observing how fluid properties such as velocity, pressure, and density change over time. It involves tracking these changes at fixed observation points, allowing for the analysis of flow patterns and behaviors within a defined volume of space. This method is particularly useful for examining large-scale phenomena such as cyclones or currents without needing to follow individual fluid particles.
Lagrangian Description
Conversely, the Lagrangian approach centers around individual fluid particles. It follows the motion of these particles as they travel through the fluid, capturing their trajectory and how their properties evolve over time. This method can be especially insightful when examining smaller scale interactions, such as turbulence or vortex formations, where the path of the individual particles is of primary interest.
Key Differences
- Eulerian: Fixed points in space; measures how properties change over time at these points.
- Lagrangian: Follows individual particles; tracks their paths and changes in properties.
Both descriptions complement each other and offer valuable insights depending on the specific fluid dynamics under examination.
Youtube Videos

![Lagrangian Description and Eulerian Description [Fluid Mechanics]](https://img.youtube.com/vi/27m1I-DlOik/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eulerian and Lagrangian Descriptions
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let me take you very concept wise that the angular rotations, the rate of rotation of the fluid element about the point P will be the average angular velocity,...
Detailed Explanation
In fluid mechanics, there are two main ways to describe the motion of fluids: Eulerian and Lagrangian. The Eulerian approach focuses on specific locations in space and observes how fluid properties (like velocity) change over time at these locations. In contrast, the Lagrangian approach tracks individual fluid particles as they move through space over time. Understanding both descriptions helps analyze fluid flow from different perspectives.
Examples & Analogies
Think of a river (Eulerian) where you observe how fast the water moves at a certain bridge over time, compared to a boat (Lagrangian) where you consider how the boat itself moves down the river. This analogy shows how the same fluid motion can be interpreted in different ways.
Fluid Elements and Virtual Fluid Balls
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The fluid element which is representing a certain space of the fluid particles which is much larger scale than the molecules levels... and this is easy concept that how much of displacement will be there, how much of translations will be there.
Detailed Explanation
A fluid element can be thought of as a virtual fluid ball that occupies a specific volume of fluid. When we analyze these fluid elements, we can describe their motion through translations (movement in space) and rotations (spinning around an axis). The size of these fluid elements is larger than individual molecules, allowing us to see overall fluid behavior rather than molecular interactions.
Examples & Analogies
Imagine a soccer ball rolling down a hill. The ball represents a fluid element. The path it takes as it rolls (translation) and the way it spins (rotation) are similar to how fluid elements behave in a flowing liquid.
Displacement and Velocity Components
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
At the ∆t time, after the ∆t times, these particles which is there it can move it at a displacement of u into ∆t, v into ∆t, w into ∆t...
Detailed Explanation
When tracking fluid particles, we analyze their displacement based on their velocity components in the x, y, and z directions. The relationship is straightforward: displacement is calculated by multiplying the velocity by the time interval. By understanding how far the particles move in each direction during a small time period, we can better predict the overall motion of the fluid element.
Examples & Analogies
Consider walking your dog. If you walk at a certain speed (velocity), the distance you and your dog will cover in a fixed time can be calculated easily. For instance, if you walk at 3 meters per second for 5 seconds, you'll cover 15 meters. This concept is similar for individual fluid particles in motion.
Rotation and Angular Velocity
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
See if I take it this is the fluid element okay, it will have the velocity variations that means... the fluid particles is going to rotate it, is it correct?
Detailed Explanation
Fluid elements can also rotate about an axis, which is described by angular velocity. When different parts of a fluid element have varying velocities, this results in a rotational motion. This rotation can help explain phenomena such as whirlpools or eddies in water, where different sections of fluid spin at different speeds.
Examples & Analogies
Think of a washing machine. As the clothes spin around, different sections of the fabric may move faster or slower than others, creating a complex rotating motion. This is similar to how fluid elements rotate when there are velocity gradients within a fluid.
Deformations in Fluid Elements
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So basically if you look at that the fluid can go through 2 types of motions; translations and rotations also, it can have a deformations of linear strains and the shear strain.
Detailed Explanation
Fluid elements can undergo deformations due to stresses acting on them. These deformations manifest as linear strains (length changes) and shear strains (changes in shape). Understanding these types of stress helps predict how fluids behave under different conditions, which is crucial for various engineering applications.
Examples & Analogies
Consider stretching a rubber band. When you pull it (a linear strain), it gets longer. If you twist it (a shear strain), its shape changes. Similarly, fluids expand or deform under pressure, helping us understand flow behavior in pipes or natural bodies of water.
Vorticity and Rotation Measurement
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, if you want to have very detailed derivations... how the complex processes are happening it, how the mixing of water and air is happening it.
Detailed Explanation
Vorticity is a measure of the local rotation of a fluid at a given point, defined mathematically as the curl of the velocity fields. It provides insight into the rotational movement and structure of fluid flow, helping us understand how fluids interact and mix, such as in turbulent flow conditions.
Examples & Analogies
Imagine a whirlpool in a lake. The swirling water creates a specific rotational flow pattern, and by measuring how quickly the water rotates, you can determine the vorticity in that region. Observing vorticity gives scientists crucial insights into the dynamics of fluid flows.
Key Concepts
-
Eulerian Description: Focuses on fixed points while observing fluid properties.
-
Lagrangian Description: Follows the path of individual fluid particles.
-
Velocity Field: Describes the distribution of velocity in the fluid across different points.
-
Fluid Deformation: Changes in fluid shape and volume due to forces acting in the flow.
Examples & Applications
Analyzing weather patterns can be achieved more easily using the Eulerian approach by tracking changes at specific monitoring stations, rather than following air mass particles throughout their journey.
The interaction of particles in a small stream can be effectively studied using the Lagrangian description, allowing researchers to observe how individual leaves or debris follow different paths based on currents.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Euler views the flow, at a fixed point, don't you know? Lagrangian’s path we follow, fluid particles, both proud and hollow.
Stories
Imagine a river with two friends, Euler and Lagrangian. Euler stands still by the bank, measuring the speed of the water, while Lagrangian hops in a boat, tracing the currents around.
Memory Tools
To remember Eulerian and Lagrangian: E = Examine Every point; L = Locate Each particle.
Acronyms
E-L = Eulerians observe; Lagging particles travel.
Flash Cards
Glossary
- Eulerian Description
An approach in fluid mechanics that focuses on observing the fluid properties at fixed points in space over time.
- Lagrangian Description
An approach that follows individual fluid particles to analyze how their motion and properties change over time.
- Velocity Field
A representation of how the velocity of fluid varies in space, often described using scalar and vector functions.
- Fluid Deformation
The change in shape or size of a fluid element resulting from stress or changes in flow conditions.
Reference links
Supplementary resources to enhance your learning experience.
