Vorticity and Rotational Elements
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll start by discussing vorticity. Can anyone tell me what vorticity measures in a fluid?

Does it measure how much the fluid is rotating?

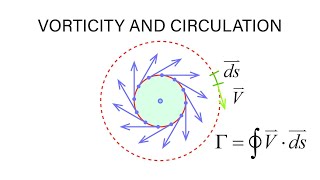
Exactly! Vorticity measures the local rotation of fluid particles. Vorticity is mathematically defined as the curl of the velocity vector field. Can anyone explain why this might be important?

It could help us understand how fluids behave in different scenarios, like during storms.

Absolutely! Understanding vorticity can help predict weather patterns and much more.
Fluid Motion: Translation and Rotation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s look at how fluid particles can either translate or rotate. What do we mean by these terms?

Translation means moving from one place to another, right?

Correct! And what about rotation?

Rotation would involve spinning about an axis.

Exactly. In fluid motion, both translations and rotations are influenced by velocity fields. Remember the mnemonic 'T-Ro-V', which stands for Translation-Rotation-Velocity. It can help you remember these relationships!
Calculating Angular Velocity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's shift our focus to angular velocity. Does anyone know how we can relate it to vorticity?

Isn't vorticity just twice the angular velocity?

Exactly right! Vorticity is defined as the curl of the velocity vector, which relates directly to the angular velocity of the fluid. The formula is essential for applications in fluid dynamics.

So, if we know the vorticity, we can determine how fast a fluid is spinning?

Precisely! Vorticity gives us crucial insights into the rotational behaviors of fluid flows.
Understanding Fluid Deformations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s analyze how fluids deform. We have two main types of deformation: linear strain and shear strain. Can anyone define linear strain?

It's the rate of increase in length per unit length.

Correct! And shear strain involves what concept?

The angle change between two lines that were perpendicular before.

Exactly! Both types of strain are critical for understanding the mechanics of fluid flow.
Practical Examples of Vorticity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s look at some real-world applications. Who knows how vorticity can help us understand cyclones?

Vorticity can explain the rotation of the air in the cyclone, right?

That's correct! Cyclones are a prime example of how understanding vorticity allows us to predict their behavior and impact. It's fascinating!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the concepts of vorticity and motion of fluid elements are explored in detail, covering both translational and rotational motions. The section emphasizes the understanding of fluid movements, vorticity calculations, and their real-world applications, particularly in analyzing vortex formations.
Detailed
Vorticity and Rotational Elements
In fluid mechanics, vorticity is a key concept that refers to the measure of the local rotation of the fluid at a point. It is defined as the curl of the velocity vector field, conveying how fast and about which axis the fluid is swirling. Vorticity plays a crucial role in understanding fluid motions, especially in complex flows such as those found in weather patterns and ocean currents. Additionally, this section discusses the types of movements fluid elements can undergo—namely translations and rotations. Translations refer to the movement from one point to another, characterized by velocity components in various directions (x, y, z). Meanwhile, rotations describe the angular motion about a point, wherein the change in velocity gradients can lead to angular velocity.
The section also covers how deformations occur within fluid elements, emphasizing the linear and shear strain that result from velocity gradients. These phenomena are essential in analyzing fluid dynamics comprehensively. For practical understanding, examples of vortex formations, such as those occurring in the Bay of Bengal, are introduced, demonstrating the relevance of vorticity in real-life applications.
Youtube Videos
![What you need to know about Vorticity [Fluid Mechanics]](https://img.youtube.com/vi/Xu5IT4bL-v8/mqdefault.jpg)


![Vorticity Explained Conceptually [Aero Fundamentals #67]](https://img.youtube.com/vi/X-hgPslzTcc/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Motion
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
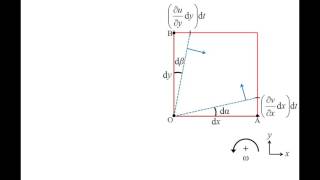
Fluid can experience two types of motions: translations and rotations. Translations occur when fluid particles move from one location to another based on the velocity components in various directions. Rotations occur around a point, influenced by the velocity fields.
Detailed Explanation
In fluid mechanics, when we discuss motion, we primarily look at how fluid particles behave. Translations refer to the shift of fluid particles from Point A to Point B. This movement is governed by the velocity components (e.g., u, v, w) in different directions. On the other hand, rotations refer to how fluid particles spin around a point, which is affected by variations in velocity. If a particle experiences different velocities at different points (e.g., velocities at the left and right of the particle), it may begin to rotate.
Examples & Analogies
Think of a leaf floating on a pond. If the current (representing velocity) moves the leaf, it translates across the water. However, if there's a swirl in the water (like a mini vortex), the leaf will start to spin, illustrating the concept of rotation.
Angular Velocity and Fluid Rotation
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The rate of rotation of a fluid element is known as angular velocity. It is influenced by the velocity variations within the fluid, and can be computed from the difference in velocities at various points.
Detailed Explanation
Angular velocity measures how fast a fluid element is rotating around a point. It involves looking at the differences in velocity at various locations of the fluid element. By calculating the differences in velocities between points around the fluid element, we can determine how quickly and in what direction it is rotating. This is often expressed in terms of angular rates describing how much rotation occurs in specific planes (e.g., xy, xz, and yz planes).
Examples & Analogies
Imagine a merry-go-round. As children spin it faster or slower at different points, the whole structure rotates. The varying speeds around the center represent the angular velocity of the system.
Linear Strain Rate
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The linear strain rate refers to the rate at which the length of a fluid element changes due to variations in velocity across different points of the fluid. If the velocity varies, parts of the fluid will stretch or compress.
Detailed Explanation
Linear strain rate is a measure of how much the length of a fluid segment changes due to different velocities at each end. For example, one end of a fluid element might move faster than the other, leading to a stretching effect. This occurs when there are velocity gradients in the fluid flow. The formula to calculate linear strain rate depends on the initial length and the change in length over time. If the velocities are constant and uniform, there will be no change in length.
Examples & Analogies
Think about a rubber band. If you pull on both ends at different speeds, the band stretches unevenly, demonstrating how fluid elements can experience strain under varying velocities.
Shear Strain Rate
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Shear strain rate is the measure of the angular changes in a fluid element's shape as different parts of it move at different velocities, leading to deformation.
Detailed Explanation
Shear strain rate quantifies how the angle between two lines changing due to the movement of particles within the fluid. For instance, if two originally perpendicular lines within a fluid element start to slide past one another due to different velocities, the angle between them shifts—this is shear strain. The equation takes into account the velocities in two perpendicular directions and how they cause angular deformation. This can lead to complex flow patterns in fluids.
Examples & Analogies
Consider a deck of cards being pushed sideways. The cards will shift from their flat arrangement, changing angles as they slide over one another. This behavior mimics how fluid elements deform under shear strain.
Vorticity Measurement
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity measures the local rotation of a fluid particle and is mathematically defined as the curl of the velocity vector field. It effectively quantifies how much and how quickly a fluid element is rotating around a point.
Detailed Explanation
Vorticity is an important concept in fluid dynamics that helps us understand the rotational behavior of fluid particles. Mathematically, it is the curl operation applied to the velocity field of the fluid. This means that vorticity provides a snapshot of how fast and in what direction the fluid is rotating at any given point. If the vorticity is zero, it indicates no local rotation, suggesting that the fluid flow is irrotational.
Examples & Analogies
Think of a tornado. The swirling motion of air can be described using the concept of vorticity. The more intense the vorticity, the stronger and more organized the rotation, akin to how the winds spiral around the tornado's core.
Key Concepts
-
Vorticity: A measure of rotation in fluid elements.
-
Angular Velocity: Related to vorticity and defines the speed of rotation.
-
Translation: Movement of fluid particles in a straight path.
-
Rotation: Angular motion about a point in the fluid.
-
Strain: Indication of deformation due to fluid motion.
Examples & Applications
In cyclonic weather systems where the air rotates around the center, vorticity is critical in predicting weather patterns.
Water flowing from a narrow pipe into a wider one experiences linear strain as the fluid expands due to decreasing velocity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Vorticity spins, it's not a fuss, it tells how fluids whirl, creating a rush!
Stories
Once a water droplet traveled through a pipe, it spun faster and faster as it hit a bend, quickly swirling into a vorticity vortex, demonstrating how fluid movement is never dull.
Memory Tools
T-Ro-V for Translation-Rotation-Velocity helps in remembering fluid motions.
Acronyms
V.O.R.T for Vorticity, Angular Velocity, Rotation, Strain - key aspects of fluid mechanics.
Flash Cards
Glossary
- Vorticity
A measure of the rotation of fluid elements in a flow field; mathematically represented as the curl of the velocity vector.
- Angular Velocity
The rate of rotation of an object; in fluid dynamics, derived from vorticity.
- Translation
The linear movement of fluid particles from one location to another.
- Rotation
The circular movement of fluid particles about an axis or point.
- Linear Strain
Rate of increase in length per unit length of a fluid element.
- Shear Strain
The change of angle between two initially perpendicular lines intersecting in a fluid element.
Reference links
Supplementary resources to enhance your learning experience.
