Linear Strain Rate
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to talk about linear strain rate, which is the rate of increase of length per unit length in a fluid element. This concept is vital in fluid mechanics as it reflects how fluid elements deform under different velocities.

Why is it important to understand the strain rate in fluids?

Great question! The strain rate helps us predict how a fluid will behave in various conditions, especially when it experiences shear or compressive forces.

So, are we saying that if the velocity changes, the fluid also changes shape?

Exactly! If there's a difference in velocity between two parts of the fluid element, it can stretch or compress, leading to a linear strain. This can further affect the overall flow characteristics.
Calculating Linear Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To calculate the linear strain rate, we consider the initial length of a fluid segment and the change in length due to velocity differences. Do you remember how we can express this mathematically?

Is it the change in length divided by the original length?

Right! The linear strain rate is defined as the increase in length divided by the original length. This ratio gives us a dimensionless number which is essential for analyzing different fluid situations.

What happens if the fluid is incompressible? Does the strain rate change?

Good point! If the fluid is incompressible, while it can still stretch, the volume of the fluid remains constant. Therefore, the calculations must account for this incompressibility in evaluating strain rates effectively.
Examples of Linear Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's look at an example where fluid flows from a smaller pipe to a larger one. Here, as the fluid expands to fill the larger area, it experiences a linear strain. Can anyone explain what this would look like?

It stretches as it enters the larger pipe, right? So it would have a positive linear strain?

Exactly! And conversely, if it were to flow into a smaller diameter pipe, the fluid would compress, resulting in a negative strain. Understanding these changes is crucial for engineers.

How does this impact design decisions in civil engineering?

Excellent inquiry! Engineers must consider strain rates when designing systems to ensure fluid dynamics are effectively managed, influencing pipe size, material choice, and flow rates.
Interrelation of Strain and Shear Rates
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s connect linear strain rates with shear strain rates. How do these two concepts interact during fluid motion?

I think shear strain happens when layers of the fluid slide past each other, right? So wouldn’t that affect the linear strain as well?

Absolutely! The shear strain can change the linear dimensions of the fluid element. If shear strains cause different layers to move at varying velocities, the resultant changes can lead to both linear and volumetric strains.

Are there formulas to correlate these two types of strain?

Yes! The strain rate tensor is a great way to express the relationship mathematically, encompassing both shear and linear strain rates all within the fluid context.
Conclusions and Summary
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To sum up, linear strain rates play a fundamental role in how we understand fluid dynamics, affecting everything from flow designs to mechanical integrity. What would you say is the main takeaway from today’s session?

That strain rates influence how fluids deform and that this is crucial for engineering applications.

And that we need to account for both shear and linear strain together for a complete understanding.

Also, knowing the difference between conditions like compressible and incompressible flow helps in making better design choices.

Well said! Those are excellent points and will aid your further studies in fluid mechanics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Linear strain rate is defined as the rate of increase in length per unit length within a fluid element. The discussion elaborates on how the strain rate affects fluid volume and movement, particularly in situations of varying velocities across the fluid elements.
Detailed
Linear Strain Rate
In fluid mechanics, the concept of linear strain rate is critical for understanding how fluids behave under motion and deformation. It is defined as the rate of increase in length per unit length within a fluid element, representing the change in length of a segment of fluid over time, particularly as influenced by velocity variations within the fluid. The movement of fluid particles from one point to another, coupled with differences in velocity at those points, results in a linear strain where lengths of fluid segments change. In this context, positive strain indicates an increase in length while negative strain signifies a decrease, essential for analyzing fluid dynamics in varying conduits and boundary conditions. Additionally, the section establishes the relationship between linear strain rates, shear strain rates, and the volumetric changes in fluid elements under flow conditions. This understanding lays the groundwork for further exploration into fluid kinematics and dynamics.
Youtube Videos
![How To Calculate Linear Strain Rate Value [Fluid Mechanics]](https://img.youtube.com/vi/7G2w2zDTlAQ/mqdefault.jpg)







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Linear Strain Rate
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
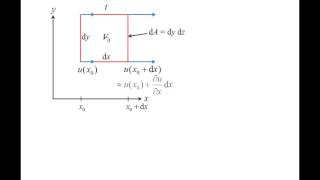
The linear strain rate is defined as the rate of increase in length per unit length.
Detailed Explanation
The linear strain rate quantifies how much an object elongates as a result of applied stress. Specifically, it measures the change in length of a fluid element relative to its original length. If a fluid segment stretches, the difference in velocity between its ends leads to a change in its length, producing a strain.
Examples & Analogies
Imagine stretching a rubber band. If you pull the rubber band at both ends, it gets longer. The linear strain rate can be likened to the amount the rubber band stretches relative to its original size — it shows how quickly and significantly the rubber band changes as you pull.
Fluid Element Movement
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
At point P, you have a velocity V, but at point Q, you may have a different velocity. At time dt, point P will move to P' and point Q will move to Q'.
Detailed Explanation
As fluid flows, different points within the fluid element can move at different speeds due to velocity gradients. For instance, if a fluid element stretches, point P may experience a slower velocity compared to point Q. This differential movement causes a stretching effect, leading to strain.
Examples & Analogies
Think about two ice skaters holding hands while gliding on the ice. If one skater slows down while the other continues at the same speed, their distance apart changes. Similarly, in fluid mechanics, when points in a fluid element move at different velocities, it results in stretching between them.
Positive Linear Strain in Incompressible Flow
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When a flow is incompressible, the net volume of the fluid element remains constant, even as it stretches.
Detailed Explanation
In incompressible flow, while the shape of the fluid element can change (leading to strain), the overall volume of the fluid remains constant. This means that any increase in length is balanced by corresponding changes in other dimensions. As a result, while fluid might elongate, it does not lose or gain fluid — it is merely redistributing its volume.
Examples & Analogies
Consider a balloon. If you stretch it to make it longer, the balloon's width will decrease to keep the amount of air constant inside. The volume does not change, but the shape does. This is similar to how incompressible fluid flow behaves.
Computing Linear Strain Rate
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
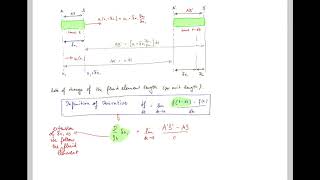
We can compute the linear strain rate as the change in length of a fluid element divided by its original length.
Detailed Explanation
To calculate the linear strain rate, you take the change in length of the fluid segment and divide it by its initial length. This gives you a ratio that represents how much the segment has stretched relative to its starting size. In mathematical terms, it is typically denoted as ε̇, where ε̇ = (ΔL) / L0, with ΔL as the change in length and L0 as the original length.
Examples & Analogies
Imagine a piece of clay rolled into a cylinder. If you pull the ends of the cylinder apart, its length increases. You could measure the new length and compare it to the original length to find out how much it has stretched. This ratio helps illustrate the concept of strain in a tangible way.
Strain Rate in a Pipe Flow
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When a fluid particle moves from a smaller diameter pipe to a larger diameter pipe, it experiences linear strain.
Detailed Explanation
In practical fluid mechanics, when fluid moves through a pipe with varying diameters, the particles near the sides of the pipe may reach different velocities compared to those in the center. This difference causes some particles to travel farther than others, leading to stretching and strain within the fluid. Hence, as the diameter of the pipe increases, the flow must adjust, resulting in strain.
Examples & Analogies
Think of water flowing from a narrow garden hose into a wider bucket. As the water transitions from the hose (smaller diameter) to the bucket (larger diameter), the speed of water near the hose's end may vary compared to water near the center of the bucket. This difference in flow speeds illustrates how linear strain rate can be observed in real-world scenarios involving fluid dynamics.
Key Concepts
-
Linear Strain Rate: A measure of the increase in length per unit length in a fluid element under varying velocities.
-
Shear Strain Rate: The angular distortion occurring between layers of fluid in motion.
-
Incompressible Flow: Conditions where the fluid density is unaffected by external changes, allowing for constant volume.
Examples & Applications
Example of fluid moving from a narrow pipe into a wider section, illustrating how linear strain affects flow velocity and fluid shape.
Example of a fluid contracting when transitioning from a wider pipe to a narrower one, highlighting negative strain in the process.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When strain rates show growth, fluid's length does boast!
Stories
Imagine a balloon that stretches; with every breath, it elongates in syncing bursts, just as fluid expands in flowing thirst.
Memory Tools
To remember linear strain, think 'Length in Change' - L in C.
Acronyms
S.L.E. - Strain Length Energy distinguishes the key concepts of strain in fluid phenomena.
Flash Cards
Glossary
- Linear Strain Rate
The rate of increase in length per unit length, reflecting the deformation of fluid elements.
- Strain
The measure of deformation representing the displacement between particles in a material body.
- Shear Strain Rate
The rate at which angular distortion occurs in a fluid element, typically due to shear stress.
- Incompressible Flow
A flow condition where the fluid density remains constant despite changes in pressure and velocity.
Reference links
Supplementary resources to enhance your learning experience.
