Shear Strain Rate and Deformation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Deformation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore how fluid elements deform under motion. Can anyone tell me what we mean by deformation in the context of fluids?

Is it how the shape or size of the fluid changes when it moves?

Exactly! Deformation can be linear or shear. Linear deformation relates to changes in length, while shear deformation involves angles changing between lines. Let's remember: 'Length changes, goes Linear; Angles change, that's Shear!'

How do we measure these deformations in fluid mechanics?

Good question! We measure deformation rates, like shear strain rate, which is the change in angle per unit time. Let's say it together: 'Shear means shift in shape!'
Shear Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The shear strain rate is vital in fluid dynamics. It’s the half-rate of angular changes between two initially perpendicular lines. Can anyone provide an example?

When fluid flows past an obstacle, it can create shear strain between the fluid layers, right?

That's correct! And we can calculate the shear strain using velocity gradients. Here's a mnemonic to remember: 'Shear Strain, Frame to Aim.'

What happens if there's a large shear strain?

If the shear strain is significant, it can lead to turbulence in the fluid flow, affecting its behavior. Keep that in mind!
Angular Velocity and Deformation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's transition to angular velocity, which is crucial for understanding fluid motion. Can anybody recall what angular velocity measures?

It measures how fast a fluid particle is rotating, right?

Exactly! The angular velocity relates to the rotation of fluid elements caused by velocity differences. A quick aid to remember: 'Rotate Slow, Angular Flow!'

How is this rotation different from shear strain?

Great follow-up! Rotation involves an entire fluid element turning, while shear is about shape adjustments without full rotation. Let’s refrain: 'Rotate with speed; Shear takes heed.'
Practical Applications of Strain Rates
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Understanding these deformation concepts has real-world implications. For instance, in civil engineering, when designing water conduits, why is it crucial to consider strain rates?

To ensure that the structure can handle the fluid flow without failing, right?

Exactly! Strain rates affect structural integrity. Remember, 'Plan for Flow, Fail not to Grow!'

What about in natural disasters, like cyclones?

That's an insightful connection! Cyclonic flow involves complex shear strains and rotational velocities. So, studying these concepts helps predict such events.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explores shear strain rates, linear and shear strain deformations in fluid mechanics. It emphasizes the significance of fluid motion, angular velocity, and how these concepts are applied in analyzing fluid behavior in different scenarios.
Detailed
In this section, we delve into the concepts of shear strain rate and deformation within the realm of fluid mechanics. The shear strain rate is defined as the rate of change of the angle between two lines due to fluid motion, while deformation encompasses linear and shear strains. The section discusses how fluid elements experience translation and rotation due to changes in velocity fields, causing both linear and shear strains. A clear distinction is made between rotational effects and shear deformation, highlighting the importance of velocity gradients. Understanding these concepts is fundamental for analyzing complex fluid behaviors, including vortex formation and fluid dynamics in various applications.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept of Fluid Elements
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let me take you back to the basic fluid mechanics. I talked about fluid elements representing a certain space of fluid particles. These particles are much larger than molecular levels and can be conceptualized as virtual fluid balls.
Detailed Explanation
Fluid elements are used to simplify the understanding of fluid motion. They represent a cluster of fluid particles that can exhibit various types of motion, such as translation (movement from one place to another) and rotation (spinning around a point). The concept allows us to analyze fluid flow without having to account for individual molecules, making our calculations much more manageable.
Examples & Analogies
Think of a fluid element like a volume of water in a swimming pool. Just as that volume of water can move smoothly from one end of the pool to another, a fluid element can translate through a flow field, helping us describe how the water behaves without focusing on every single water molecule.
Translations and Rotations of Fluid Elements
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When the fluid element experiences motion, it can translate or rotate. Translation occurs when fluid particles move from one position to another in space, and rotation occurs when a fluid element spins around a point.
Detailed Explanation
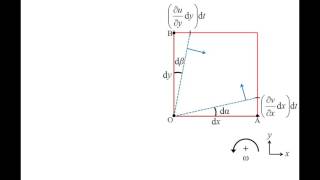
Translation of fluid particles is caused by differences in velocity in different directions, calculated as displacement over time. For rotation, we need to consider how velocity components differ across the fluid element, which results in angular velocity. Angular velocity measures how fast a fluid particle is spinning around a central point.
Examples & Analogies
Imagine a group of children holding hands in a circle (the fluid element). If one child starts running while still holding hands, the whole group translates (moves) across the playground. If the children start spinning in place, they are rotating. The different speeds at which the children run or spin represent the different velocity components in a fluid.
Strain in Fluid Elements
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
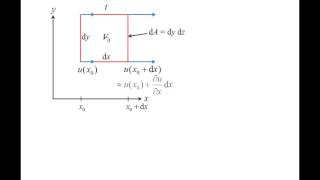
Now, let's focus on deformations in fluid elements. Fluid elements can undergo linear strain (elongation) and shear strain (distortion). Linear strain occurs when a fluid element stretches, and shear strain occurs when it deforms angularly.
Detailed Explanation
Linear strain is defined as the rate of change in length per unit length. It happens when the velocity at one part of the fluid element differs from another part, causing it to elongate. Shear strain measures how much a fluid element distorts in shape without changing its volume. The difference in velocity within the fluid element is crucial for understanding how these deformations occur.
Examples & Analogies
Think about stretching a rubber band. When you pull it, you can see it elongate (linear strain). If you twist it while pulling at both ends, you create a different shape (shear strain). Both actions illustrate how fluids can stretch and distort in flow.
Shear Strain Rate
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The shear strain rate refers to the rate at which the angle between two intersecting lines changes during deformation. It quantifies how much deformation occurs as a fluid flows, represented as a function of velocity gradients.
Detailed Explanation
Shear strain rate is defined mathematically as half the rate of change of the angle between two initially perpendicular lines that intersect at a point. When a fluid element deforms, the angle between these lines can change, indicating shear deformation. This rate can be expressed in terms of velocity gradients, which define how quickly the velocity changes across the fluid element.
Examples & Analogies
Imagine two lines drawn on a piece of paper, initially intersecting at a right angle (90 degrees). If you push one line while keeping the other fixed, the angle between them will change. This change in angle is similar to the shear strain rate; it shows how fluid elements can twist and deform under stress.
Vorticity and Its Relation to Fluid Rotation
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vorticity is a vector that measures the rotation of fluid particles and is represented as the curl of the velocity field. It quantifies how much and in which direction the fluid is rotating.
Detailed Explanation
Vorticity is defined as the curl of the velocity vector field, which mathematically correlates with the rotation of fluid particles. It serves as an indicator of the fluid's rotational characteristics. A high vorticity value implies that the fluid is swirling strongly, while a vorticity of zero indicates no rotation at that point. This concept illustrates how rotation influences fluid dynamics.
Examples & Analogies
Consider a whirlpool in water. The stronger the whirlwind, the higher the vorticity. Just as the water spins rapidly around the center, a fluid with high vorticity indicates a strong rotational motion, helping characterize the flow's behavior.
Key Concepts
-
Shear Strain Rate: A measure of how the angle between two lines changes as the fluid moves.
-
Linear Strain: Represents the change in length of a fluid element due to velocity differences.
-
Angular Velocity: Indicates the rotational speed of fluid particles within the flow.
Examples & Applications
Consider fluid flowing through a tapered pipe: as it narrows, points in the fluid at the inlet experience different linear strain due to velocity changes across the fluid cross-section.
In a tornado, the swirling motion creates significant shear strain rates and deformation in the surrounding air.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Shear strain shifts, while linear lifts.
Stories
Picture a river flowing through a landscape: it expands through different terrains, representing linear strain, and twists around curves, symbolizing shear strain.
Memory Tools
SLASH: S for Shear, L for Length, A for Angular, S for Strain, H for How they change!
Acronyms
BASE
for Ball
for Angular
for Shear
for Efforts in deformation.
Flash Cards
Glossary
- Deformation
Changes in the shape or size of a fluid element due to motion.
- Shear Strain Rate
The rate of change of angle between two initially perpendicular lines within a fluid element.
- Linear Strain
The change in length per unit length in a fluid element.
- Angular Velocity
The rate of rotation of a fluid particle around a defined point.
Reference links
Supplementary resources to enhance your learning experience.
