9.4.2.1. Translations

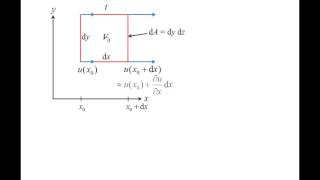
Now, come to the translations which is very easy concept okay, which is the velocity factor which is responsible for shifting a fluid particle from A location to B locations, it depends upon the velocity components like in this case, you have a small u, v and w is a scalar velocity component in x, y, z directions respectively.

In fluid mechanics, the motion of fluid particles can be understood by the concept of translations, which refers to the movement from one point to another due to velocity. Each fluid particle has velocity components in three dimensions: x, y, and z, represented as 'u', 'v', and 'w'. The velocity indicates how quickly a particle moves in each direction. For example, if a fluid particle is at point A and moves to point B, the distance it travels in the x, y, and z directions can be calculated using these velocity components over a specific time period (Δt). Hence, the translation is determined by multiplying each velocity component by the time duration, giving us the new position of the particle.

Imagine a boat drifting on a river. If the boat moves downstream, its position changes based on the speed of the current (the velocity 'u'). If it's also swaying side to side (the velocity 'v'), the movement can be understood in three dimensions, similar to how fluid particles translate in a flowing medium.

So, that way it will move in these 3 directions to get a new positions factors, so it is a simply translations from A point to the B point with y the velocity vector components, okay that means this particles has the velocity vector component u, v, w and at the t time, t plus delta t time, it will move it with a in the x direction would be u∆t and v∆t and w∆t from these origins locations.

The displacement of a fluid particle due to translations can be mathematically expressed using the formula for displacement. If a fluid particle has a velocity in the x direction (u), y direction (v), and z direction (w), the displacement in each direction can be calculated over a small time interval (Δt). The total displacement can thus be expressed as: x displacement = u * Δt, y displacement = v * Δt, and z displacement = w * Δt. By taking into account the velocity components for the respective directions, we can pinpoint the new position of the particle after the time period has passed.

Suppose you are riding a bike on a straight road at a steady speed. If you go for 5 minutes (Δt), your distance traveled in the forward direction depends on your speed (u). If you also make a turn, your position changes in both the forward direction (u * Δt) and sideways (v * Δt). By calculating both, you find exactly where you end up after that duration.

Now, coming to the rate of rotations, which is called angular velocity okay, what could be the angular velocity of the fluid point. See if I take it this is the fluid element okay, it will have a this the velocity variations...

Angular velocity refers to the rate of rotation of a fluid particle around an axis. In fluid mechanics, if a fluid element experiences varying velocities at different points, it will tend to rotate. For example, a fluid particle influenced by other nearby moving particles will have its angular velocity determined by the differences in the velocity components at these points. These variations lead to rotational motion around a central axis, with angular velocity defined mathematically based on these differences in motion.

Picture a merry-go-round. When one person pushes it, different points on the edge will move at different speeds. The faster those point velocities vary, the faster the merry-go-round spins. Similarly, fluid particles behave in a way where their rotating motion is influenced by the speed variations around them.

Now, coming to the very simple thing is called linear strain rate that means, what is the strain rate; rate of increase the length per unit length, this is very simple definition...

In fluid mechanics, the linear strain rate quantifies changes in a fluid element's length as it flows. Essentially, it measures how much longer or shorter a fluid element becomes over time due to velocity gradients. If one section of the fluid moves faster than another, the distances between them change, leading to stretching or compressing of the fluid segment. This is essential in understanding deformation within the fluid as it flows through different geometries or under varying forces.

Imagine stretching a rubber band. If you pull one end faster than the other, the rubber band elongates unevenly. This action reflects similar principles seen in fluid mechanics where sections of fluid stretch or compress depending on the forces and velocities acting within.

So, we can compute it what would be that is why we can easily compute it, what it will be linear strain rate which is the gradient of the linear strain rate in the x directions, the y directions and the z direction...

The shear strain rate is determined by how the angle between fluid elements changes as they move past one another under shear stress. It is the rate of angular change when a segment of fluid is displaced. As different layers of fluid slide over each other, they experience differing velocities. This differential motion can be represented mathematically and is crucial in predicting how various fluid mixtures will respond to different flows during operations like mixing or pumping.

Think of applying pressure to a deck of cards by pushing one side. The top cards slide over the bottom ones, creating an angle change between them. This behavior is analogous to how fluid layers experience shear strain, essential for understanding laminar and turbulent flows.

--