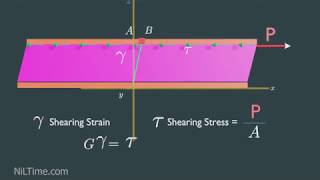
Shear Strain Rate
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Shear Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re discussing the concept of shear strain rate, which helps us understand how fluids deform under shear stress. Does anyone know what strain rate means?

Isn't it the rate of deformation relative to time?

Exactly! The shear strain rate is specifically about angular changes in the shape of a fluid element. For example, if we have two parallel plates, the fluid between them experiences changes in shape as the plates move relative to each other.

So, if the fluid particles are moving at different velocities, they stretch out?

Yes, precisely! This difference in velocity leads to linear strain, which we'll cover next. One way to remember this is by thinking of the acronym 'S.T.R.A.I.N.' for Shear rate, Time, Rate of deformation, Angular change, Influence on flow, and Non-uniformity.

That's a good acronym!

Let's summarize: shear strain rate is a measure of how much a fluid element deforms due to velocity differences. Keep this in mind as we move forward!
Mathematics of Shear and Linear Strain Rate
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's delve into some key equations for shear and linear strain rates. Can anyone remind me how we calculate the linear strain rate?

Is it the change in length over the original length?

That's right! The linear strain rate can be described as the difference in velocity between two points divided by the distance between them. This is fundamental for understanding how fluids respond to forces.

And how is shear strain rate related?

The shear strain rate is concerned with how angles between parts change. For two lines intersecting in a fluid element, if the angle decreases due to motion, we calculate the rate as half of that angle decrease over time. Remember, a simple way to think about it is: 'Less angle = More strain'.

So we’re measuring how much the angle 'shears' during motion?

Exactly! This is why different fluid properties matter. To wrap up, the equations for both shear and linear strain rates allow us to quantify how fluids react to applied forces.
Vorticity and Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about vorticity. Can someone explain what vorticity is in the context of fluid mechanics?

Isn’t it the rotation of fluid particles?

That's correct! Vorticity quantifies how much a fluid particle rotates around an axis. This is essential when we study complex flows, such as in turbulence.

How do we calculate it?

Vorticity is defined as the curl of the velocity field. In simple terms, if you take the differential element of velocity, you can determine how rotation changes across the flow. Keep in mind that vorticity increases with faster flows!

So vorticity and strain rate are related?

Yes, they are! Both are influenced by velocity gradients. To summarize, vorticity helps describe how particles may spiral or rotate within a flow, which is crucial for modeling fluid dynamics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explains shear strain rate as a critical concept in fluid mechanics, exploring how velocity gradients influence the shape and motion of fluid elements. It delves into the differences between linear strain, shear strain, and the importance of these concepts in analyzing fluid flow. Vorticity is also introduced as a measure of the rotation of fluid particles.
Detailed
Detailed Summary
This section focuses on Shear Strain Rate in fluid mechanics, describing how fluid elements deform when subjected to shear stress. It begins by defining shear strain rate and its relationship with velocity gradients, illustrating how the difference in velocities at two points leads to elongation (linear strain) in a fluid element.
Key Points Covered:
- Linear Strain Rate: Defined as the rate of increase of length per unit length in fluid flow. It highlights that if two points in the fluid (Point P and Point Q) experience different velocities, the distance between them changes, leading to strain.
- Shear Strain Rate: Explained as the half of the rate of decrease of the angle between two initially perpendicular lines intersecting within a fluid element. This concept emphasizes how fluid layers sliding past one another cause deformation.
- Vorticity and Angular Velocity: Introduced as the measure of a fluid particle's rotation, vorticity is defined as the curl of the velocity vector field. It serves as an essential concept for understanding turbulence and vortex formation.
- Mathematical Representations: The section discusses various equations that define the volumetric strain rate and shear strain rate in Cartesian coordinates, highlighting how these relate to the velocity gradients.
The significance of understanding these concepts lies in their application to real-world scenarios, such as analyzing fluid flow in pipelines or under varying pressure conditions.
Youtube Videos


![Concept of Fluid Shear Strain Rate [Fluid Mechanics]](https://img.youtube.com/vi/D7BTKwz2UWY/mqdefault.jpg)

![How To Calculate Shear Strain Rate Value [Fluid Mechanics]](https://img.youtube.com/vi/j4kjZpHDr2I/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Basics of Shear Strain Rate
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
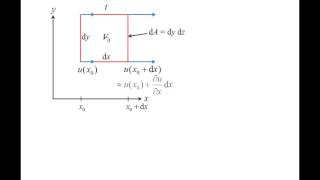
Now, coming to the very simple thing is called linear strain rate that means, what is the strain rate; rate of increase the length per unit length, this is very simple definition, okay. So, rate of increase in length for unit length that means, let you have a the initially, you have a the fluid element which is starting from P to Q okay, at the point P you have the velocity \(v_p\) but at the Q, we should have a based on the Taylor series, you can have this velocity \(v_q\).
Detailed Explanation
The shear strain rate is defined as the rate at which deformations occur in a material (in this case, fluid). It is specifically the change in length (more accurately, the change in relative displacement) per unit length caused by the velocity differences across points in the fluid. For example, if two points P and Q are in a fluid flow and they move apart because of differing velocities, we can say that the rate of strain is determined by how quickly they stretch apart relative to how far apart they were initially. This is important in fluid mechanics as it helps us understand how fluids deform under flow conditions.
Examples & Analogies
Imagine a group of students holding hands in a line as they run forward. If the students at the front run faster than those at the back, they'll start to stretch apart, illustrating how one part of the group experiences more strain than another. This stretching represents the shear strain rate as some parts 'move' away from others while still being connected.
The Concept of Linear Strain in Fluid Flow
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
At the dt times, these P point will be moved to Ṕ, the Q point will move to Q́, the distance between these 2 will the different, so that is the reasons they will be linear strain. Distance travelled by this P and Q will be the different as the velocities are the different at the P and Q, if the velocity difference between the PQ not there, then you will may not have a linear strain, will not have a linear strain.
Detailed Explanation
As the fluid flows, the velocities at different points will often vary. This causes points P and Q (which were originally at the same distance apart) to now be farther apart after a given time interval (dt). This differential movement means the fluid element experiences stretching, known as linear strain. If both points P and Q move at the same rate, then there is no strain because they maintain their relative positions.
Examples & Analogies
Think of a rubber band. If you pull both ends at the same rate, it simply stretches uniformly. However, if you pull one end faster than the other, the part of the band closer to the faster end stretches more than the part nearest the slower end, creating strain. This illustrates how variations in velocity can lead to differential strain in a fluid.
Implications of Incompressibility in Fluid Flow
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since, there is a velocity variation, the fluid element which connected as a virtual fluid balls from P to Q; Q moves more as compared to the P, so you have a stretching of fluid virtual fluid balls, stretching of the virtual fluid balls that means, they will stretch it, there will be the same dimensions but there will be stretching it, so they are will be elongated as the width will be reduces, the length will be change it.
Detailed Explanation
In incompressible flow, despite the fact that the density remains constant, the fluid still undergoes deformation. As certain parts of the fluid accelerate faster, the overall dimensions of the fluid elements may change. It leads to an elongation in the direction of flow while possibly compressing in transverse directions. Understanding these changes is crucial for predicting fluid behavior.
Examples & Analogies
Visualize a balloon filled with water. If you push on one side of the balloon faster than the other, the water nearest your push moves quicker and stretches out, while the areas a bit farther from the push compress slightly. The result is the fluid dynamically adjusting and changing shape, though the total volume remains consistent, which reflects how incompressible flow behaves.
Introduction to Shear Strain Rate
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
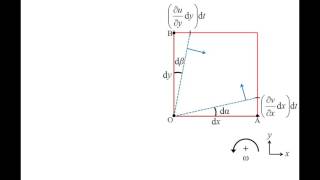
The shear strain rate is a half rate of decrease of angle between 2 initially perpendicular lines that intersect at the point. What it is saying that if you look at these figures that I have a figure like this, the fluid element at the t1 time at the fluid element at the t time. At the t time, this line is moving \(\theta_1\) and \(\theta_2\) angles.
Detailed Explanation
The shear strain rate focuses on angular changes within a fluid element. It looks at how the angle between two lines (initially perpendicular) changes due to shear stress. As shear forces act on the fluid, these angles shift, contributing to the fluid's deformation. The shear strain rate quantifies this angular change over time, reflecting how quickly and in what manner the fluid becomes distorted.
Examples & Analogies
Imagine a piece of clay resting on a table. If you push one side of the clay, the shape changes, but at the same time, the angle between two edges of the clay changes from the flat angle. Just like the clay, fluids experience changes in shape and angle when forces are applied, which is captured in the concept of shear strain rate.
Components of the Strain Rate Tensor
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, as of now we have done it, we can get a shear strain rate in a Cartesian coordinate for different plane, xy plane, zx plane and yx plane and finally, we can write the shear strain rate tensor which will be linear strain formations and the formations of shear strain rate. So, it has a 9 component of stress strain rate tensors.
Detailed Explanation
In fluid mechanics, we can represent how a fluid deforms using a strain rate tensor, which captures the variations in strain across different directions. This tensor has components for different planes: xy, xz, and yz planes. Each component represents how the fluid stretches or compresses in that particular direction, allowing us to mathematically describe the fluid's response to forces.
Examples & Analogies
Envision a stretchy fabric that can be pulled in different directions. Depending on how you pull it, the fabric will stretch more along certain lines than others. Similarly, the strain rate tensor acts like a map of how fluid responds to different strain directions, providing a comprehensive tool for analyzing fluid behavior in response to forces.
Key Concepts
-
Shear Strain Rate: Measures how much a fluid deforms due to shear stress.
-
Linear Strain Rate: Rate of increase in length per unit length.
-
Vorticity: Measures spin of fluid particles, crucial for understanding turbulence.
Examples & Applications
When fluid flows through a pipe that narrows, the velocity changes, leading to shear strain as the fluid stretches.
In a rotating fluid, such as in a cyclone, vorticity is high, indicating a strong rotational motion.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When fluids flow and layers shift,
Stories
Imagine a thick syrup between two plates. As the plates move apart, the syrup stretches and swirls. This represents shear strain rate, while the swirling motion illustrates vorticity.
Memory Tools
Remember 'S.T.R.A.I.N' - Shear rate, Time, Rate of deformation, Angular change, Influence on flow, Non-uniformity.
Acronyms
Use 'V.S.S.' to remember
Velocity
Shear
Strain.
Flash Cards
Glossary
- Shear Strain Rate
The rate of change of shape of a fluid element due to shear stress, often involving angular deformation.
- Linear Strain Rate
The rate of change in length per unit length experienced by a fluid element.
- Vorticity
A vector field that describes the local spinning motion of a fluid at a point; it is the curl of the velocity field.
- Velocity Gradient
The change in velocity with respect to spatial position, critical in calculating strain rates.
- Fluid Element
A small mass of fluid used to analyze flow characteristics in fluid mechanics.
Reference links
Supplementary resources to enhance your learning experience.
