Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Welcome everyone! Today we’re introducing the Navier-Stokes equations, which are crucial in understanding fluid dynamics. Can anyone tell me who contributed to their development?
I think Claude-Louis Navier and George Stokes were involved.
That's right! They developed these equations independently to describe fluid motion. The Navier-Stokes equations help to model complex fluid flow problems. What does anyone think makes these equations significant?
They help predict how fluids behave, which is essential for engineering applications!
Exactly! The equations give us insights into various fluid properties and motions. Let’s remember the acronym 'NST' for Navier-Stokes Theory, which encompasses their foundational role in fluid mechanics. Now, can anyone summarize what types of fluids these equations primarily describe?
They describe Newtonian fluids primarily!
Good job! Now let's explore Newtonian versus non-Newtonian fluids and why understanding this difference is crucial.
Key Assumptions in Navier-Stokes Equations
Unlock Audio Lesson
In our earlier discussion, we touched on the types of fluids involved. What assumptions do we make about the fluid when applying the Navier-Stokes equations?
We assume the fluid is incompressible and flows isothermally?
Correct! Assuming incompressibility means that the fluid's density remains constant. What can you tell me about isothermal flow?
In isothermal flow, the temperature is constant throughout the fluid.
Excellent! These assumptions simplify the equations significantly. To remember these concepts, think of the acronym 'I-T', for Incompressible and Temperature constant. Can anyone explain how these assumptions help in obtaining approximate solutions?
They allow us to reduce our unknowns and make the equations easier to solve!
Exactly! By simplifying the assumptions, we can address one of the main challenges in fluid dynamics.
Complexity and Non-linearity of Navier-Stokes Equations
Unlock Audio Lesson
Let’s talk about some complexities involved with the Navier-Stokes equations. What makes solving these equations particularly difficult?
The non-linearity makes it challenging, right?
Absolutely! Non-linearity leads to multiple solutions and unstable flow conditions. Can anyone define what we mean by 'non-linear' in this context?
It means that the relationship between variables isn’t a straight line; small changes can lead to large effects.
Well explained! Keep in mind the phrase 'Small inputs don't mean small outputs.' This reflects the chaos theory principles in fluid dynamics. How does this complexity affect our modeling of fluid flows?
It means we often need computer simulations and computational fluid dynamics methods.
Exactly! Without computational methods, finding analytical solutions would be nearly impossible.
Importance of Approximate Solutions
Unlock Audio Lesson
As we wrap up, why are approximate solutions essential in fluid dynamics?
Because exact solutions are hard to come by due to the equations' complexities!
Correct! And over the years, researchers developed computational fluid dynamics techniques to get these approximate solutions. Can someone explain what CFD stands for?
Computational Fluid Dynamics!
Right! CFD is a crucial tool in engineering that uses numerical analysis to approximate the solutions of fluid flow problems. Let’s remember 'CFD = Calculators For Dynamics' as a mnemonic! Can anyone reflect on how this impacts real-world applications?
It allows engineers to design more efficient systems like airplanes and reactors by predicting fluid behavior accurately.
Excellent point! This section illustrates why mastering these concepts is vital for the engineering field.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section emphasizes the significance of approximate solutions to the Navier-Stokes equations in fluid mechanics, illustrating the historical context of their development and the necessary assumptions made for incompressible and isothermal flows. It outlines the fundamental equations and discusses the implications of non-linearity in resolving real-world fluid flow problems.
Detailed
In this section, we delve into the complexities surrounding the Navier-Stokes equations, which form the backbone of computational fluid dynamics. Originating from the independent works of Claude-Louis Navier and George Stokes, these equations describe fluid motion through mathematical expressions that account for forces acting within the fluid. The discussion moves from the foundational definitions of Newtonian and non-Newtonian fluids to key assumptions of incompressible and isothermal flow, enabling approximation methods to derive solutions. One of the primary challenges highlighted is the reduction of simultaneous unknowns—density, velocity components, and pressure—leading to the need for innovative methods, like computational fluid dynamics (CFD), due to the inherent non-linearities and complexity in the equations. The essence of this section is to illustrate why finding exact solutions is daunting, yet approximate solutions are vital for applications across various fluid flow scenarios.
Youtube Videos
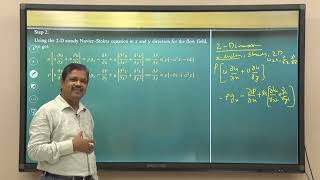
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning all of you. Today we are going to discuss about very interesting topics, the topics on Navier-Stokes equations. That is what the basic foundations of computational fluid dynamics and many of the complex fluid flow problems also we can solve it by using Navier-Stokes equations.
Detailed Explanation
The Navier-Stokes equations are fundamental in fluid mechanics. They describe how fluids (liquids and gases) move and are crucial for computational fluid dynamics (CFD). This section emphasizes the importance of these equations in understanding and solving various fluid flow problems.
Examples & Analogies
Think of a flowing river. The Navier-Stokes equations help us understand how the water moves, the speed at which it flows, and how it interacts with its banks, ensuring engineers can design bridges and dams effectively.
Historical Context
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Claude-Louis Navier and George Stokes derived the Navier-Stokes equations independently. That is what we got the Navier-Stokes equations because of these two professors from Penns and England.
Detailed Explanation
The equations are named after two notable figures, Navier and Stokes, who contributed to their development in the 19th century. Understanding the historical context helps appreciate the collaborative effort in advancing fluid mechanics, showing how scientific progress often builds on the work of others.
Examples & Analogies
Just as modern technology builds on earlier inventions—like how smartphones evolved from basic mobile phones—the Navier-Stokes equations evolved through the contributions of Navier and Stokes, leading to the advanced fluid dynamics we study today.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Also, I will talk about revisit Newtonian fluid and non-Newtonian fluid part which is quite interesting to look at how we can use for this Navier-Stokes equations.
Detailed Explanation
Fluid mechanics differentiates between Newtonian fluids, which have a constant viscosity regardless of the flow conditions (like water), and non-Newtonian fluids, which change their viscosity based on how they are stressed (like ketchup). The Navier-Stokes equations primarily apply to Newtonian fluids, making this distinction crucial for proper application.
Examples & Analogies
Imagine trying to pour honey (a non-Newtonian fluid) versus water (a Newtonian fluid). Honey flows more slowly and becomes thicker under pressure, while water flows consistently. Understanding these differences is essential when analyzing fluid behaviors in real-world scenarios.
Assumptions in Deriving the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We will talk about the derivations of Navier-Stokes equations for with assumptions of incompressibles isothermal flow.
Detailed Explanation
When deriving the Navier-Stokes equations, we often make certain assumptions, such as considering the flow to be incompressible (density changes are negligible) and isothermal (temperature remains constant). These simplifications make the equations easier to work with and applicable to many real-world situations.
Examples & Analogies
Think about blowing up a balloon. If you blow slowly, the balloon expands uniformly (incompressible). However, if you blow too hard, the air inside compresses, changing pressure and density. The equations simplify when we assume a slow, steady inflation, ignoring the complexities of compression.
Boundary Conditions and Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
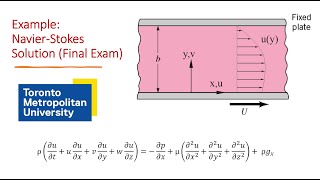
After that we can look it we can apply for an example problems with what would be the appropriate boundary conditions to solve this Navier-Stokes equations.
Detailed Explanation
Boundary conditions are essential in fluid dynamics as they define the behavior of fluids at the edges of the domain where equations are applied. Understanding and properly setting these conditions allows for accurate simulations and predictions of fluid behavior in various applications.
Examples & Analogies
Consider a swimming pool. The water's movement is affected by the walls (boundary conditions). If you were to model the water's flow, you'd need to consider how the water interacts with the walls to get accurate results, just as boundary conditions do in Navier-Stokes equations.
Challenges in Solving Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The problems is unsteady time component is there, nonlinear partial differential equations.
Detailed Explanation
The Navier-Stokes equations are complex nonlinear partial differential equations, making them challenging to solve, particularly for unsteady (time-dependent) flows. Most of the time, direct analytical solutions are not possible, leading to the need for numerical methods and approximations.
Examples & Analogies
Think of trying to predict the weather. Numerical models use complex mathematics to approximate the conditions at play since we can't directly solve all the variables involved. Similarly, engineers use computational methods to approximate fluid behavior using the Navier-Stokes equations.
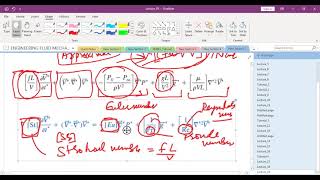
The Birth of Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That is the reasons we try to look for approximate solutions because there is no exact solutions we will get it unless otherwise very simplified cases.
Detailed Explanation
Computational Fluid Dynamics (CFD) emerged as a tool to numerically analyze fluid flow since exact solutions to the Navier-Stokes equations are rare. CFD allows us to simulate fluid behavior across complex geometries and conditions, enabling advanced engineering applications.
Examples & Analogies
Just as flight simulators allow pilots to practice flying in a controlled environment without leaving the ground, CFD allows engineers to simulate fluid flows and study their behaviors without needing to conduct costly and time-consuming physical experiments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations governing fluid motion.
-
Incompressible Flow: Characteristics of flow where the density remains constant.
-
Isothermal Flow: Flow conditions with constant temperature throughout.
-
Computational Fluid Dynamics (CFD): Numerical methods for solving fluid dynamics problems.
-
Non-linearity: Issues arising in equations that complicate finding solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Navier-Stokes equations to analyze airflow over an airplane wing.
-
Applying approximate solutions in simulating water flow in pipes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow, they may bend and twist; Understanding Navier-Stokes keeps fluid dynamics on the list.
📖 Fascinating Stories
-
Imagine a river flowing smoothly (incompressible) and staying at a constant temperature (isothermal). Engineers use this scenario to predict behaviors accurately.
🧠 Other Memory Gems
-
Use 'I-T' for Incompressible and Temperature constant to remember key assumptions in Navier-Stokes.
🎯 Super Acronyms
Remember 'NST' for Navier-Stokes Theory.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe the motion of viscous fluid substances.
-
Term: Incompressible Flow
Definition:
A flow regime where the fluid density remains constant.
-
Term: Isothermal Flow
Definition:
A flow regime in which the temperature of the fluid remains constant.
-
Term: NonNewtonian Fluids
Definition:
Fluids that do not follow Newton's law of viscosity, displaying variable viscosity with changes in shear rate.
-
Term: Computational Fluid Dynamics (CFD)
Definition:
A branch of fluid mechanics that uses numerical analysis and algorithms to solve and analyze problems involving fluid flows.
-
Term: Convective Accelerations
Definition:
Accelerations experienced by fluid parcels as they move through the flow field.
-
Term: Local Accelerations
Definition:
Accelerations at a point in the flow due to time-dependent changes in velocity.
-
Term: Stress Tensor
Definition:
A mathematical representation of the internal forces in a fluid.