Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Incompressible Flow
Unlock Audio Lesson
Good morning everyone! Today, we are discussing the assumptions necessary for deriving the Navier-Stokes equations. Let's start with what we mean by 'incompressible flow.' Can anyone tell me what that means?
Does it mean the fluid's density doesn't change?
Exactly! Incompressible flow assumes that density remains constant. This simplifies our equations because we don’t have to account for variations in density due to pressure or temperature changes. This typically applies to liquids and low-speed gas flows. Can anyone think of a scenario where we assume fluid flow is incompressible?
Like water flowing through a pipe?
Great example! As water flows through a pipe at relatively low speeds, we can safely assume it’s incompressible. In many engineering applications, this assumption is critical. Let's remember the acronym 'IC' for 'Incompressible Constant' to help us recall this assumption.
The Importance of Isothermal Conditions
Unlock Audio Lesson
Now, let’s turn to the assumption of isothermal flow. What do you think this means, Student_3?
I think it means the temperature of the fluid stays the same?
Exactly! Isothermal flow means that the temperature within the fluid remains constant during flow. Why do you think this is helpful in our fluid dynamics equations?
It keeps the viscosity constant too, right?
Yes! When the temperature is constant, the fluid's dynamic viscosity doesn't change, making our calculations much simpler. It’s crucial in scenarios like heat exchangers where temperature gradients can heavily influence flow. A mnemonic to remember this could be 'IT's COLD' — Isothermal Temperature Constant On Low Dynamics!
Connecting Assumptions to Navier-Stokes Equations
Unlock Audio Lesson
So now that we've covered incompressibility and isothermal conditions, let’s link these assumptions back to the Navier-Stokes equations. Who can explain how these principles simplify the equations?
I think if the density stays constant, we don't have to consider density changes in our momentum equations.
Correct! This allows us to eliminate density as a variable in many cases. Not only does this simplify the equations, but it also helps us focus on viscous and pressure forces. Can someone give me an example of where we might apply these equations with these assumptions?
In analyzing airflow over a flat surface, right?
Exactly right! When studying airflow over wings or flat surfaces at low speeds, we often assume incompressible and isothermal conditions to predict behavior accurately. Let’s use the acronym 'IC - IT' to summarize: Incompressible and Isothermal - key assumptions for simpler Navier-Stokes!
Reviewing Key Points
Unlock Audio Lesson
Before we finish up today, let’s review what we’ve learned. Student_3, can you summarize what we discussed regarding incompressible flow?
Sure! We learned that in incompressible flow, the fluid's density is constant, which helps us simplify our calculations.
That’s right! And how about isothermal flow, Student_1?
Isothermal flow means the temperature stays the same, which keeps the viscosity of the fluid constant as well.
Fantastic! So when we combine these assumptions, they help us derive the Navier-Stokes equations more effectively. Remember 'IC - IT' as both help us remember essential assumptions for simplifying fluid dynamics problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the key assumptions underlying the derivation of the Navier-Stokes equations, emphasizing the concepts of incompressible and isothermal flows. These assumptions help simplify complex fluid dynamics into solvable equations.
Detailed
Assumptions for Deriving Equations
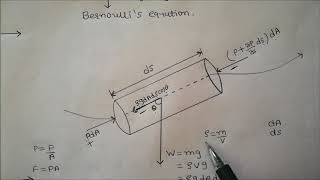
In fluid mechanics, the derivation of the Navier-Stokes equations relies on a few critical assumptions. Primarily, we consider the flow to be incompressible and isothermal.
Incompressible Flow
An incompressible flow assumes that the fluid's density remains constant, meaning it does not change with varying pressure or temperature within the given domain. This assumption is valid for many low-speed flows where density variations are negligible. By keeping the density constant, we simplify the equations significantly, allowing us to focus on momentum transfer without worrying about complex density changes.
Isothermal Flow
Isothermal conditions indicate that the temperature of the fluid remains constant throughout the motion. This implies that the dynamic viscosity of the fluid also remains stable, making the analysis of viscous effects more straightforward. An isothermal assumption allows the use of steady-state analysis, further reducing computational complexity.
Implications for Navier-Stokes Equations
These assumptions lead to the formulation of the Navier-Stokes equations as they highlight two main forces acting on the fluid:
1. Viscous forces: Resulting from internal friction within the fluid.
2. Pressure forces: Associated with the fluid's static pressure.
Understanding these assumptions is crucial for applying the Navier-Stokes equations to real-world scenarios in fluid dynamics, such as predicting airflow patterns or fluid behavior in various engineering applications.
Youtube Videos
![Common assumptions in fluid mechanics [Fluid Mechanics #3b]](https://img.youtube.com/vi/kimMbNP9DrY/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
First is incompressible flow okay. That means density more or less fairly okay does not change with space as well as time. That means it is a constant. It is a constant. That is the flow is called incompressible flow.
Detailed Explanation
In this chunk, we discuss the assumption of incompressible flow in fluid mechanics. This means that the density of the fluid remains nearly constant as it moves through space and time. In practical terms, when we say a fluid is incompressible, we imply that changes in pressure do not significantly alter its density. Examples of fluids that can usually be treated as incompressible include liquids like water. This assumption greatly simplifies the mathematical modeling of fluid flow, as it allows us to use continuity equations without having to account for variations in density.
Examples & Analogies
Think about a balloon filled with water. If you squeeze the balloon, the volume of water does not change; instead, it just shifts to areas where there is more space. This behavior illustrates the incompressibility of liquids, which helps engineers calculate how water flows through pipes.
Isothermal Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Next is that iso thermal as flow. So thermal means you can indicate it is a temperature. Isothermal means within the fluid domain, temperatures remain more or less constant. That means within the fluid domain, we are not considering it that there is a temperature change. That is what a significant order of change of the temperatures.
Detailed Explanation
This chunk explains the assumption of isothermal flow, which posits that the temperature within the fluid remains constant throughout the flow process. This is particularly significant when analyzing flows where heat exchange with the surroundings is minimal. Maintaining constant temperature simplifies the analysis of fluid properties such as viscosity, which can change with temperature. Therefore, if the temperature of the fluid remains fairly constant, we can treat viscosity as a constant value during our calculations.
Examples & Analogies
Imagine taking a long drive on a hot day with your windows down. The air inside your car remains warm and stable despite the wind. If you were to consider that air as an isothermal fluid, it would mean that the temperature of the air does not change significantly as you move through different environments, which simplifies understanding its flow behavior.
Importance of Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I have a these two assumptions okay this great simplifications of fluid flow problems okay. So if you look at that and go through very details book is there but it is quite higher level book okay of fluid mechanics by Kundu, Cochin and Dolling...
Detailed Explanation
In this chunk, the speaker highlights the significance of making the assumptions of incompressible and isothermal flow. These assumptions are crucial because they simplify complex fluid dynamics problems into more manageable equations. With incompressible and isothermal assumptions, the governing equations can often be solved more easily, leading to clearer insights into fluid behavior, such as predicting how a fluid will flow in a certain environment or around obstacles. The speaker also references advanced texts that expand on these concepts but emphasizes that understanding basics is key.
Examples & Analogies
A common analogy is a simplified view of calm water in a swimming pool. If you neglect temperature fluctuations and assume that water has a consistent thickness (dense), calculations become straightforward. You're left to focus merely on other factors like gravity, pressure, and flow direction instead of accounting for varying densities due to temperature changes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Incompressible Flow: Density remains constant, simplifying equations.
-
Isothermal Flow: Temperature remains constant, leading to stable viscosity.
-
Navier-Stokes Equations: Describe fluid motion, focusing on pressure and viscous forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing through a closed system, like pipes or nozzles, where density does not change.
-
Air flow over an aircraft wing at low speeds, where temperature variations are negligible.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Incompressible flow holds steady, Density's constant, keep it ready.
📖 Fascinating Stories
-
Imagine a river where the water flows smoothly; no rocks and temperature stays warm. That's incompressible and isothermal, making fluid flow easier to analyze.
🧠 Other Memory Gems
-
Remember 'IC - IT' for Incompressible & Isothermal for fluid flow assumptions.
🎯 Super Acronyms
IC for Incompressible Constant; IT for Isothermal Temperature.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Incompressible Flow
Definition:
A flow where the fluid's density remains constant throughout.
-
Term: Isothermal Flow
Definition:
A flow where the temperature of the fluid remains constant during its motion.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations that describe the motion of fluid substances.