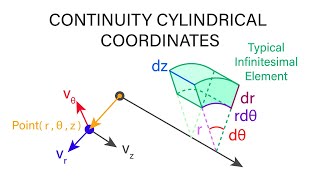
Cylindrical Coordinates
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cylindrical Coordinates
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning class! Today we are going to explore cylindrical coordinates, which are vital for various applications in fluid mechanics. Can anyone remind me why we need different coordinate systems?

I think it's because certain problems are easier to solve in different systems based on their geometry.

Exactly! Cylindrical coordinates allow us to represent 3D space using a radius, angle, and height. This system is particularly effective for problems involving cylindrical symmetry.

So in what cases would we use cylindrical coordinates instead of Cartesian?

Great question! We often use cylindrical coordinates for flows around pipes, jets, or any scenario where the geometry has circular symmetry, allowing easier application of Navier-Stokes equations. Remember the acronym 'RAT' - Radius, Angle, and Height, to help remember these core components.

What do these coordinates look like mathematically compared to Cartesian?

Good point! In cylindrical coordinates, a point is given as (r, θ, z), where 'r' is the radial distance from the origin, 'θ' is the angle around the z-axis, and 'z' is the height. Let's dive deeper into how we can transform equations of motion in these coordinates.

Can we go through an example of a cylindrical coordinate transformation?

Absolutely! If we consider a point at (x, y, z), we can convert to cylindrical coordinates using: r = √(x² + y²), θ = tan⁻¹(y/x), and z remains unchanged. This transformation is useful when dealing with Navier-Stokes equations in cylindrical flow.
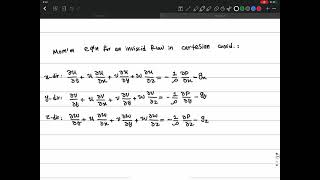
Cylindrical Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's now look at how the Navier-Stokes equations are represented in cylindrical coordinates. Students, can anyone explain what these equations address?

They describe the motion of fluid substances and include considerations for forces acting on the fluid.

Correct! When taking the cylindrical form, we adjust for radial and angular motions instead of x and y. For example, we will have terms such as ∂u/∂r and ∂u/∂θ, reflecting how velocity changes concerning radius and angle.

How does this impact the solutions we can find?

It allows us to model fluid flow more accurately in cylindrical geometries. You may run into forms like 'u' being the velocity in the radial direction, while 'v' could represent the angular velocity. Remember 'RADIAL for motion' - meaning you focus on the radial components in these problems.

Are there additional terms in cylindrical coordinates compared to Cartesian?

Yes, indeed! There may be extra terms like the centrifugal and Coriolis forces introduced in these coordinate systems, which aren't present in Cartesian coordinates. It widens the scope of dynamics we can analyze.

Could we summarize how to approach problems in cylindrical coordinates?

Absolutely! Approach them by first identifying the symmetry of the problem, converting your coordinates, applying Navier-Stokes equations in cylindrical form, and reassuring yourself to include all relevant forces. Lastly, practice makes perfect!
Applications of Cylindrical Coordinates
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss practical scenarios where we apply these concepts. Can anyone think of real-world systems that utilize cylindrical coordinates?

I think about liquid flowing through pipes or the behavior of jets.

Right on point! For example, the flow of oil, water, or any fluid through cylindrical pipes can be effectively modeled using cylindrical coordinates. Remember the phrase 'PIPE FLOW for cylindrical' to connect these ideas!

What about issues involving boundary layers around cylindrical objects like ships?

Excellent thought! The flow characteristics around a cylindrical object significantly affect drag and other forces. This principle applies to the design of various marine and mechanical systems.

Are there any environmental or natural occurrences where these equations apply?

Definitely! Analyzing tornadoes or whirlpools in water bodies is another notable example, where vortex flows can be assessed effectively using cylindrical coordinates.

Why is it advantageous to use these cylindrical approaches?

Using cylindrical coordinates reduces complexity when simulating phenomena with circular symmetry, enabling clearer insights and more manageable calculations. Always keep in mind 'CIRCLES simpli-fy motions.'

Can we conclude with key takeaways about cylindrical coordinates?

Sure! Remember that cylindrical coordinates are vital for analyzing fluid flows in circular geometries, allow for the application of the Navier-Stokes equations with adjusted variables, and have numerous applications in both engineering and natural systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we delve into the importance of cylindrical coordinates in fluid mechanics, specifically how they facilitate the formulation and solving of the Navier-Stokes equations, allowing for effective analysis of fluid flow problems through transformation of equations into a more manageable form.
Detailed
Detailed Summary of Cylindrical Coordinates
Cylindrical coordinates are crucial in fluid mechanics, particularly in the context of the Navier-Stokes equations. This section discusses how the transformation from Cartesian coordinates to cylindrical coordinates can simplify the analysis of fluid flows and computational solutions. By representing points in space with a radial distance, angle, and height, we can better model certain physical situations, such as flows around cylinders or pipes. The equations for mass conservation and momentum conservation adapt accordingly, leading to modified forms that accommodate the geometry of the problem. Understanding these transformations and the resulting equations is essential for effective fluid dynamics analysis.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Cylindrical Coordinates
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, we can apply the Navier-Stokes equations in cylindrical coordinates. This is particularly useful in scenarios where the geometry of the problem has cylindrical symmetry.
Detailed Explanation
Cylindrical coordinates are a three-dimensional coordinate system that extends the two-dimensional polar coordinates by adding a height dimension. In this system, a point in space is represented by three coordinates: the radial distance from the origin (r), the angular coordinate (θ), and the height (z). This coordinate system is particularly beneficial for problems with circular geometries, such as flow in pipes, and allows for the simplification of the Navier-Stokes equations.
Examples & Analogies
Consider a garden hose. The flow of water through the hose can be analyzed using cylindrical coordinates, as the hose has a circular cross-section. By using r to represent the distance from the center of the hose, θ for the angle around the hose, and z for the length of the hose, we can better understand the water's flow patterns and pressures within.
Equations in Cylindrical Coordinates
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Navier-Stokes equations in cylindrical coordinates are more complex than those in Cartesian coordinates but follow a similar form, adapting for the new coordinates.
Detailed Explanation
In cylindrical coordinates, the Navier-Stokes equations account for the radial, angular, and vertical flow components. This means that rather than having simple derivative terms, the equations incorporate additional terms that relate to how the flow behaves in the radial and angular directions. The forms of the equations include local accelerations, convective accelerations, pressure gradients, and viscous stress components. Each term must be specifically tailored to reflect the nature of fluid flow in a cylindrical context.
Examples & Analogies
Imagine a spinning carousel at a fair. As it spins, people on the edge experience both radial (inward towards the center) and tangential (along the carousel's edge) forces. Similarly, in fluid flow through a pipe, different forces act on the fluid moving in radial and angular directions, which need to be understood through the modified Navier-Stokes equations in cylindrical coordinates.
Applications of Cylindrical Coordinates
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The application of cylindrical coordinates is prevalent in modeling flow in pipes, tanks, and around cylindrical objects.
Detailed Explanation
Cylindrical coordinates are essential for accurately modeling fluid dynamics in systems where flow and geometry exhibit cylindrical symmetry. For example, the flow of liquid through a pipe can be effectively modeled by focusing on the radial and angular components of fluid motion. This approach simplifies calculations and helps predict how pressure changes and flow velocities behave within the pipe, enabling engineers to design better piping systems and optimize fluid transport.
Examples & Analogies
Consider a water pipe system under pressure. Engineers need to understand how water flows through various sections of pipes which can change in diameter. Cylindrical coordinates allow them to model the pressure and velocity changes along the sections of the pipes, ensuring efficient design that minimizes leaks and maximizes flow rate.
Key Concepts
-
Cylindrical Coordinates: Useful for modeling cylindrical symmetries in fluids.
-
Navier-Stokes Equations: Core equations describing fluid motion.
-
Geometry of Flow: Importance of understanding the shape and nature of flow problems.
-
Coordinate Transformation: Moving from Cartesian to cylindrical coordinates simplifies certain types of equations.
Examples & Applications
Modeling the flow of water through a cylindrical pipe using cylindrical coordinates provides a more straightforward analysis of the flow characteristics.
Observing tornado formations in cylindrical coordinates allows for a better understanding of the motion's dynamics in a natural phenomenon.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In cylindrical flow, we find our way, With radius and angle, we model the spray.
Stories
Imagine a water hose spraying in a circle, guided by the radial distance, angle, and a straight height.
Acronyms
CAP - Coordinates Apply to Pipes.
Flash Cards
Glossary
- Cylindrical Coordinates
A three-dimensional coordinate system defined by a radius, angle, and height, suitable for analyzing symmetry in fluid flows.
- NavierStokes Equations
A set of equations that describe the motion of fluid substances, incorporating forces acting on the fluid.
- Radial Distance
The straight line distance from the origin to a point in cylindrical coordinates.
- Pressure Gradient
The rate of change of pressure in spatial derivatives, influencing fluid flow.
Reference links
Supplementary resources to enhance your learning experience.
