Control Volumes and Forces
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning everyone! Today we will begin our exploration of control volumes in fluid mechanics. Can someone tell me what a control volume is?

Isn't a control volume an imaginary volume in which we analyze fluid flow?

Exactly! Control volumes help us analyze the entire system by focusing on the mass, momentum, and energy within a specific region. Now, what are the forces acting on a fluid inside a control volume?

There are body forces, like gravity, and surface forces, such as pressure and shear stress.

Correct! These forces play a critical role in how fluids move and behave. Let's remember: 'Body forces involve mass, surface forces involve area.'

How do we express these forces mathematically?

Great question! We express forces mathematically using the Navier-Stokes equations, which we will derive next. Recall Newton's law: force equals mass times acceleration.

In summary, we've discussed the definition of control volumes and identified the key forces acting within them: body forces and surface forces.
Derivation of Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s talk about the derivation of the Navier-Stokes equations. Who can explain the significance of Navier and Stokes in fluid mechanics?

They independently developed the equations that describe how fluids behave.

Correct! Their work allows us to address complex fluid behavior. The Navier-Stokes equations describe the conservation of momentum for a fluid control volume. What components make up these equations?

They include terms for velocity, pressure, and viscous forces.

"Exactly! We often categorize forces into local accelerations, convective accelerations, and changes due to pressure gradients. Let's remember:
Understanding Forces
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today’s topic is the types of forces that act within our control volumes. What types can you remember?

Body forces and surface forces, right?

Yes! Body forces act throughout the fluid volume, while surface forces affect only the fluid's boundary. Can anyone give an example of each?

Gravity is a body force, while pressure is a surface force.

Great examples! Now, let’s think of a mnemonic to help us remember: 'Big Beautiful Oceans Suction'. This reminds us of Body forces pushing down like gravity and Surface forces acting everywhere, like pressure!

What about how these forces influence fluid motion?

Both force types interact to determine fluid acceleration and flow rates. If you’re ever confused, remember: 'Force shapes Flow!' to clarify the connection between forces and fluid behavior.

To summarize, today we've identified body and surface forces and discussed how they govern fluid dynamics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section examines control volumes in fluid dynamics, how they relate to forces acting within fluids, and outlines the derivation of the Navier-Stokes equations based on Newton's laws. The innovations of Navier and Stokes in formulating fluid equations applicable in various conditions are highlighted, along with essential concepts like velocity divergence and the relation between shear stress and fluid behavior.
Detailed
Control Volumes and Forces
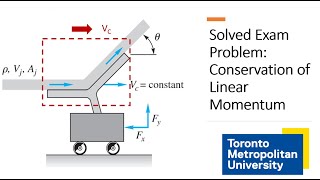
In fluid mechanics, control volumes are defined regions in space through which fluid can flow. The analysis of these volumes helps us understand the dynamics of fluid motion, particularly how forces are applied both internally and externally. This section delineates how fluid motion can be described using control volumes by integrating mass, momentum, and energy balances.
Key Concepts:
- Control Volume: An arbitrary fixed volume in space through which fluid can flow. The dynamics within this control volume are influenced by forces applied to the fluid inside it.
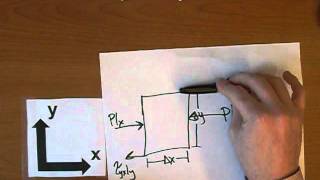
- Forces in Fluid Dynamics: Two main categories of forces are identified: body forces (like gravity) and surface forces (which include pressures and shear stresses).
The Navier-Stokes equations, which arise from the application of Newton's second law to fluid motion, express the balance of these forces and can be derived with specific assumptions concerning flow conditions (incompressible and isothermal). These equations are fundamental in computational fluid dynamics (CFD) applications and for solving complex fluid flow problems.
The derivation leads to important relationships between the various physical quantities, most notably involving velocity (u, v, w), pressure gradients, and viscous forces, making it critical for understanding fluid behavior in engineering applications.
Youtube Videos


![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fluid mechanics deals with the study of forces and motions involving fluids, and control volumes are a key concept in analyzing fluid dynamics. Control volumes are defined regions in space through which fluid may flow. In fluid mechanics, we examine the forces acting on control volumes to understand their behavior under different conditions.
Detailed Explanation
Control volumes are imaginary boundaries that help us analyze how fluids behave. When we look at fluids, it's important to capture what happens inside a specified region of space. By defining a control volume, we can focus on the mass and momentum changes due to forces acting on the fluid inside this volume. Essentially, we’re looking at how much fluid comes in and out of this volume and what forces are at play during this process.
Examples & Analogies
Imagine a large aquarium. You can define the aquarium as a control volume. You can study how fish swim (forces at play) and how water enters or exits through the filter. By focusing on this defined space, you can understand the movement of water and fish dynamics without having to analyze the entire ocean.
Forces Acting on Control Volumes
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Forces acting on control volumes are classified into two main categories: body forces and surface forces. Body forces act throughout the volume of the fluid (like gravity), while surface forces act at the boundary of the control volume (such as pressure and shear stresses).
Detailed Explanation
When analyzing control volumes, we must consider the forces that influence the motion of the fluid. Body forces are distributed throughout the fluid without requiring contact; gravity is a typical example. Surface forces, on the other hand, arise from interactions with surrounding surfaces, such as pressure from the walls of the container or friction from flow past a solid boundary. Understanding these forces is critical in predicting the behavior of fluids.
Examples & Analogies
Think of a balloon filled with water. The weight of the water exerts a body force due to gravity pulling down on it. If you press on the surface of the balloon, you're applying a surface force that can cause the water to shift or push against the sides of the balloon.
Momentum and Control Volumes
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, the Cauchy equations describe the motion of fluids within control volumes. These equations relate the net forces acting on the fluid to the changes in momentum within the volume. The principles of mass and energy conservation also apply to these control volumes.
Detailed Explanation
The Cauchy equations capture the relationship between forces and fluid motion within a control volume. By applying the equations of mass and momentum conservation, we can derive expressions to calculate how fluid speeds change due to forces acting on it. The equations incorporate both local and convective accelerations, thus providing a comprehensive view of fluid dynamics.
Examples & Analogies
Consider a river flowing down a slope. As water speeds up due to gravity (a body force), it gains momentum. If you place a dam in the river, the water now experiences a change in momentum due to the forces exerted by the dam’s surface (a surface force). Analyzing this scenario is akin to managing control volumes in fluid mechanics.
Applications of Control Volumes
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Understanding control volumes and forces is essential for applications such as predicting fluid flow in piping systems, analyzing aerodynamics around aircraft, and assessing the efficiency of hydraulic systems.
Detailed Explanation
The concepts of control volumes allow engineers to design and analyze various systems where fluid dynamics play a crucial role. By studying how fluids are controlled in certain volumes, engineers can optimize designs for plumbing, vehicle aerodynamics, and even climate control systems in buildings. These analyses lead to more efficient and effective engineering practices.
Examples & Analogies
Consider how HVAC systems work in buildings. The air within a room can be considered a control volume, and understanding how air flows in and out through vents helps engineers design systems that efficiently maintain temperature and air quality. The control volumes they analyze here are crucial for ensuring comfort in living spaces.
Key Concepts
-
Control Volume: An arbitrary fixed volume in space through which fluid can flow. The dynamics within this control volume are influenced by forces applied to the fluid inside it.
-
Forces in Fluid Dynamics: Two main categories of forces are identified: body forces (like gravity) and surface forces (which include pressures and shear stresses).
-
The Navier-Stokes equations, which arise from the application of Newton's second law to fluid motion, express the balance of these forces and can be derived with specific assumptions concerning flow conditions (incompressible and isothermal). These equations are fundamental in computational fluid dynamics (CFD) applications and for solving complex fluid flow problems.
-
The derivation leads to important relationships between the various physical quantities, most notably involving velocity (u, v, w), pressure gradients, and viscous forces, making it critical for understanding fluid behavior in engineering applications.
Examples & Applications
Example of a control volume can be imagining a tank filled with water; analyzing it allows us to see how water flows in and out.
When examining a fluid parcel falling due to gravity, we see body forces like gravity acting on it while surface forces like drag act against it.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Forces acting in the flow, surface, and body tell us how. Without them, motion simply can't show!
Stories
Imagine a fish swimming through a current; its body feels the pressure of the water around it (surface force) while also being pulled down by gravity (body force). This interplay keeps it moving.
Memory Tools
Remember: 'B.S. for fluid Forces': B = Body force (like gravity), S = Surface force (like pressure).
Acronyms
C.V.F. for Control Volume Forces
= Control
= Volume
= Forces acting in.
Flash Cards
Glossary
- Control Volume
A defined region in space through which fluid can flow, allowing analysis of fluid dynamics.
- Body Force
A force acting throughout the volume of a fluid, such as gravity.
- Surface Force
Forces that act on the surface of a fluid, including pressure and shear stress.
- NavierStokes Equations
A set of equations describing how the velocity field of a fluid evolves over time under given forces.
- Incompressible Flow
A flow where the fluid density remains constant throughout the motion.
- Isothermal Flow
A flow where the temperature remains constant and does not significantly change in the fluid domain.
Reference links
Supplementary resources to enhance your learning experience.
