Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Newtonian Fluids
Unlock Audio Lesson
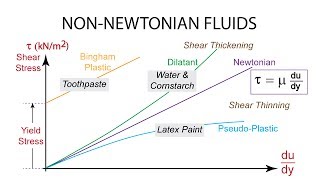
Let's start by discussing **Newtonian fluids**. These fluids have a constant viscosity and a linear relationship between shear stress and shear strain rate. Can anyone tell me what that relationship looks like mathematically?
Isn't it \( \tau = \mu \frac{du}{dy} \)?
Exactly! In this equation, \( \tau \) is shear stress, \( \mu \) is dynamic viscosity, and \( \frac{du}{dy} \) is the shear strain rate. A perfect example of a Newtonian fluid is water. Why do you think understanding this concept is important?
It helps us predict how these fluids will behave in different conditions!
Correct! This predictability is crucial in applications like pipe flow and aerodynamics.
Characteristics of Non-Newtonian Fluids
Unlock Audio Lesson
Now, let's talk about **Non-Newtonian fluids**. Unlike Newtonian fluids, they do not have a constant viscosity. Can anyone give me an example of a Non-Newtonian fluid?
Ketchup! It thickens and thins depending on how hard you shake it.
Great example! Ketchup behaves as a shear-thinning or pseudoplastic fluid, becoming less viscous under rapid stress. What implications does this have in practical situations?
It means you need to apply different forces depending on how you want to use it!
Exactly! This behavior can impact everything from food processing to material formulation.
Types of Non-Newtonian Fluids
Unlock Audio Lesson
Non-Newtonian fluids can be classified into several types. Who can name a type of Non-Newtonian fluid?
Shear-thickening fluids, like cornstarch and water!
Exactly! Shear-thickening fluids increase in viscosity with increased shear rate. What’s another type?
Bingham plastics! They need a certain amount of shear stress before they start to flow.
Yes! Bingham plastics are crucial in industries like paint production. Understanding these classifications helps engineers choose the right fluids for specific applications.
Applications of Fluid Types
Unlock Audio Lesson
Let’s discuss applications. Why is it important to differentiate between Newtonian and Non-Newtonian fluids in engineering?
Different fluids need different handling in systems, right? Like pipes or pumps?
Exactly! If an engineer does not consider the fluid type, it can lead to inefficient systems or even failures. Understanding the elasticity and flow behavior is key.
That makes sense! It’s like knowing the right tools for the job.
Spot on! Now, let’s recap. Understanding the differences between Newtonian and Non-Newtonian fluids allows engineers to predict performance and design effective systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers the definitions and key characteristics of Newtonian and Non-Newtonian fluids, explaining how they respond to shear stress. Describing the linear relationship between shear stress and strain rate in Newtonian fluids, the section contrasts this with Non-Newtonian fluids, which do not exhibit a constant viscosity.
Detailed
Detailed Summary
In this section, we explore the distinctions between Newtonian and Non-Newtonian fluids as pivotal concepts in fluid mechanics. Newtonian fluids are defined by their linear relationship between shear stress and shear strain rate, expressed mathematically as \( \tau = \mu \frac{du}{dy} \), where \( \tau \) represents shear stress, \( \mu \) is dynamic viscosity, and \( \frac{du}{dy} \) denotes the shear strain rate. Common examples include water and air, where the viscosity remains constant regardless of the rate of deformation.
Contrastingly, Non-Newtonian fluids display a complex relationship between shear stress and strain rate, where viscosity can change based on the applied stress. These fluids can be further categorized into various types, such as shear-thinning or pseudoplastic fluids (e.g., ketchup), where viscosity decreases with an increase in shear rate, and shear-thickening or dilatant fluids (e.g., cornstarch mixed with water), where viscosity increases with shear rate. The understanding of these two categories of fluids is crucial for applications in both engineering and scientific contexts, especially when employing the Navier-Stokes equations for fluid flow problem-solving.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Newtonian fluids are characterized by a linear relationship between shear stress and shear strain rate, described by Newton's law of viscosity: \( \tau = \mu \frac{dv}{dy} \), where \( \mu \) is the dynamic viscosity. Non-Newtonian fluids do not adhere to this linear relationship.
Detailed Explanation
Newtonian fluids, like water and air, maintain a consistent viscosity regardless of the flow conditions. In contrast, non-Newtonian fluids like ketchup or blood exhibit changing viscosity depending on how fast they are deformed or when subjected to shear stress. For instance, when you slowly pour ketchup out of a bottle, it appears very thick, but if you shake the bottle, it flows more easily due to the shear stress applied.
Examples & Analogies
Think of pouring honey and water. Water flows easily and consistently, demonstrating Newtonian behavior. Honey, however, thickens when you pour it slowly and becomes runnier when you shake it. This behavior is similar to non-Newtonian fluids, where viscosity changes under stress.
Characteristics of Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Newtonian fluids follow a constant viscosity that does not change with the rate of shear strain. This is crucial for many fluid dynamics applications and is governed by Newton’s law of viscosity.
Detailed Explanation
In Newtonian fluids, such as oils and gases, the shear stress is directly proportional to the shear rate. This means that if you apply a consistent force, the fluid will flow steadily. Their predictable behavior is crucial for engineering applications, such as in pipelines or lubricants, where smooth, stable flow is essential.
Examples & Analogies
Imagine trying to slide a book across the table. If the table is smooth (like water as a Newtonian fluid), it slides easily with less effort. If the table is sticky (like a non-Newtonian fluid), it becomes harder to slide the book, as the friction and resistance change based on your effort.
Understanding Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Non-Newtonian fluids exhibit varying viscosities based on the shear rate. Their behavior can include dilatant (shear-thickening) and psuedoplastic (shear-thinning) responses.
Detailed Explanation
Non-Newtonian fluids can thicken or thin when force is applied. Shear-thickening fluids, like cornstarch mixed with water (oobleck), become harder when you punch them. Shear-thinning fluids, like paint, flow more easily when stirred. Understanding these behaviors helps in industries where mixing and flow control are vital.
Examples & Analogies
Think about making ice cream with a hand mixer. At first, when you mix slowly, the ingredients blend easily. But if you mix too quickly, the mixture can become too thick and difficult to stir, similar to a shear-thickening fluid. Conversely, paint flows better when mixed, demonstrating shear-thinning behavior.
Applications of Fluid Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The distinction between Newtonian and non-Newtonian fluids is essential in various fields including engineering, medicine, and food processing. Each application relies on predicting flow behavior.
Detailed Explanation
In engineering, understanding the flow characteristics of different fluids helps design effective pipelines and systems for transporting materials. In medicine, the viscosity of blood can affect how easily it moves through vessels, influencing health treatments. In food industries, the texture and flow of sauces or drinks can determine how they are processed and packaged.
Examples & Analogies
Consider ketchup vs. mayonnaise in a restaurant. Ketchup, a non-Newtonian fluid, might require shaking to get it flowing, while mayonnaise pours steadily. Understanding these differences helps food manufacturers create products with desirable textures and consistent flow, enhancing customer satisfaction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Newtonian Fluids: These fluids have a constant viscosity, depicted by a direct relation between shear stress and shear strain rate.
-
Non-Newtonian Fluids: These fluids display variable viscosity that can change when exposed to different shear rates, leading to complex behavior in various applications.
-
Shear-thinning Fluids: Fluids that decrease in viscosity as shear rate increases.
-
Shear-thickening Fluids: Fluids that increase in viscosity as shear rate increases.
-
Bingham Plastics: These fluids do not flow until a specific yield stress is applied.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Examples of Newtonian fluids include water and air, where viscosity does not change regardless of the shear rate applied.
-
Ketchup is a shear-thinning fluid; it becomes less viscous when shaken, demonstrating complex flowing behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fluids that flow like a stream, Newtonian's dance is what we deem; But ketchup and cornstarch make a scene, Non-Newtonian’s complex cuisine!
📖 Fascinating Stories
-
Once, in a kitchen, there was a debate between water, who flowed freely in a glass, and ketchup, who thickened and needed a shake. The two learned how their behaviors varied with stress, highlighting the surprising world of fluids. Thus, the importance of understanding their properties for culinary adventures became clear!
🧠 Other Memory Gems
-
N² for Newtonian: Simple and clear; N³ for Non-Newtonian: Complex, let’s cheer!
🎯 Super Acronyms
R.E.A.C.T. for remembering fluid types
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Newtonian Fluid
Definition:
A fluid with a constant viscosity that has a linear relationship between shear stress and shear strain rate.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity can change depending on the applied shear stress.
-
Term: Shear Stress
Definition:
The force per unit area exerted on a material in a direction parallel to the surface.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to deform under shear stress.
-
Term: Shearthinning Fluid
Definition:
A type of Non-Newtonian fluid whose viscosity decreases with increased shear rate.
-
Term: Shearthickening Fluid
Definition:
A Non-Newtonian fluid whose viscosity increases with increased shear rate.
-
Term: Bingham Plastic
Definition:
A type of Non-Newtonian fluid that behaves like a solid until a certain yield stress threshold is reached.