Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Good morning everyone! Let's start by discussing the Navier-Stokes equations, which are crucial in fluid mechanics, especially in computational fluid dynamics. Can anyone tell me about the historical context of these equations?
These equations were derived independently by Claude-Louis Navier and George Stokes, right?
Correct! They independently derived these equations, which describe how fluids behave. This led to significant developments in fluid dynamics. Remember their names: Navier and Stokes—let's call them 'The Fluid Founders'.
What are some applications of these equations?
Great question! They are used in predicting weather patterns, designing aircraft, and even in blood flow analysis. Remember: Fluid Founders = Fundamental Equations.
Understanding the Basics
Unlock Audio Lesson
Let’s talk about the basics of fluid mechanics. Can anyone define what we mean by Newtonian fluids?
Newtonian fluids are those that have a constant viscosity and follow Newton's laws of viscosity. For example, water and air!
Exactly! Now, what about non-Newtonian fluids?
Non-Newtonian fluids don’t have a constant viscosity, like blood or toothpaste.
Excellent! Just remember: 'Constant Viscosity = Newtonian', 'Variable Viscosity = Non-Newtonian'.
Mathematical Foundations
Unlock Audio Lesson
Now, let’s delve into the derivation of the Navier-Stokes equations. We begin with Cauchy’s equations. Can someone explain what these equations encapsulate?
Cauchy’s equations represent the conservation of momentum for fluids, expressed in vector notation.
Yes! Momentum conservation is crucial. We calculate forces acting on a control volume by evaluating pressure and shear forces. Can someone remind me of the two components we consider?
Body forces and surface forces!
That’s right! Use the acronym 'BS' for Body and Surface forces to remember. Let's move ahead with these concepts.
Assumptions for Derivation
Unlock Audio Lesson
To derive the Navier-Stokes equations, we make several assumptions. What can we say about incompressible flow?
Incompressible flow means that the density of the fluid is constant throughout the flow.
Correct! And what about isothermal flow?
In isothermal flow, the temperature of the fluid remains constant.
Perfect! So remember: 'Incompressible = Constant Density', 'Isothermal = Constant Temperature'.
Final Form of Navier-Stokes Equations
Unlock Audio Lesson
Finally, we look at the Navier-Stokes equations themselves. What characterizes these equations?
They are nonlinear partial differential equations governing fluid motion.
Exactly! And their application is vast, but solving them can be complex due to their nonlinearity and unsteady nature. How does this connect to computational fluid dynamics?
Without exact solutions, we rely on numerical methods to approximate solutions!
Well said! Remember: 'Complexity = CFD'. This wraps up our session on the Navier-Stokes equations!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides an overview of the Navier-Stokes equations, their historical context, the mathematical foundation, and the assumptions required for their derivation, focusing on incompressible isothermal flow in various coordinate systems.
Detailed
Derivations of Navier-Stokes Equations
The Navier-Stokes equations are fundamental in fluid mechanics, essential for computational fluid dynamics. Originating from the independent works of Claude-Louis Navier and George Stokes, these equations govern the motion of fluid substances. In this section, we explore their derivation, which primarily draws upon the principles laid out in the Sinzel and Cimbala textbook, as well as foundational concepts from Newtonian physics.
Key Concepts Covered:
- Historical Context: The contributions of Navier and Stokes, explaining how they independently derived the equations, which has led to modern fluid dynamics.
- Basic Definitions: Understanding Newtonian vs. non-Newtonian fluids and the conditions under which the Navier-Stokes equations are applied, focusing on incompressible, isothermal flows.
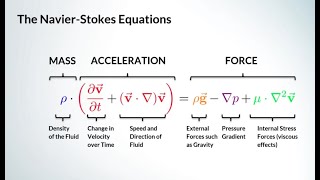
- Mathematical Derivations: Begin with Cauchy’s equations in vector form, detailing mass and momentum conservation principles through control volumes, and expanding definitions to incorporate stress tensors.
- Assumptions and Simplifications: Highlighting the approximations made to reduce complexity, including assumptions of rest for fluids leading to shear stress considerations.
- Equations in Different Coordinate Systems: Introduction to Cartesian and cylindrical coordinates and how the equations transform accordingly. The emphasis on the interrelationship between velocity, pressure, and density fields.
Through this examination, the significance of understanding these equations and their derived forms are clear, as they form the backbone of fluid mechanics and computational fluid dynamics.
Youtube Videos
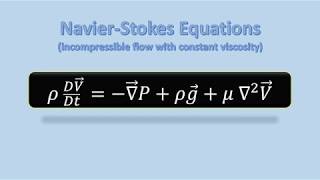
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid Mechanics
Prof. Subashisa Dutta
Department of Civil Engineering
Indian Institute of Technology-Guwahati
Lec 28: The Navier-Stokes Equation
Good morning all of you. Today we are going to discuss about very interesting topics, the topics on Navier-Stokes equations.
Detailed Explanation
In this introduction, the professor emphasizes the significance of Navier-Stokes equations in fluid mechanics, highlighting their application in computational fluid dynamics and complex fluid flow problems. The historical context of Claude-Louis Navier and George Stokes, who derived these equations independently over 200 years ago, is also presented. Their contributions form the foundation of fluid mechanics as we study it today.
Examples & Analogies
Consider the way we use equations in everyday life: similar to how the laws of physics help us understand motion and forces, the Navier-Stokes equations enable engineers and scientists to predict how fluids behave in various situations—from the gentle flow of water in a stream to the turbulent gusts of wind around a skyscraper.
Key Concepts: Newtonian vs. Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Also, I will talk about revisit Newtonian fluid and non-Newtonian fluid part which is quite interesting to look at how we can use for this Navier-Stokes equations.
Detailed Explanation
This chunk introduces two classifications of fluids: Newtonian and non-Newtonian. Newtonian fluids, like water and air, follow a linear relationship between shear stress and shear strain rate, which allows their behavior to be described using simple equations. Non-Newtonian fluids, such as blood and certain slurries, do not adhere to this linearity, requiring more complex formulations to describe their viscous behavior.
Examples & Analogies
Imagine honey versus water. When you try to pour both, honey flows more slowly and doesn’t easily follow the same rules as water. This difference in behavior exemplifies how non-Newtonian fluids (like honey) require specialized treatment compared to Newtonian fluids (like water) when using the Navier-Stokes equations.
Basic Formulations: Control Volumes and Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
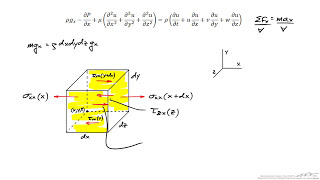
We can derive where sigma ij is a stress tensor. Now if I look at the component wise before going to these derivations, I just want to look at what is the component wise of this part.
Detailed Explanation
In fluid mechanics, the concept of a 'control volume' is essential. It involves analyzing the fluid flow within a defined volume to understand the forces acting on it. The stress tensor, denoted as sigma ij, represents the internal forces within the fluid that result from stresses, often derived from the momentum equations that form part of the Navier-Stokes equations.
Examples & Analogies
Consider a soccer ball being kicked. The area where the foot meets the ball is like a control volume. The stress (force) applied at that point causes the internal structure of the ball to respond, transmitting forces throughout it. Similarly, analyzing how fluid behaves utilizes control volumes to understand the forces acting throughout the fluid.
Breaking Down the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that what we are deriving this that we are not bringing a new physics to that. The same concept we are talking about that we know from Newton s second laws the force is equal to mass into acceleration.
Detailed Explanation
This chunk focuses on deriving the Navier-Stokes equations from established principles, specifically Newton's second law of motion: force equals mass times acceleration. The text explains that the fluid dynamics are analyzed through control volumes, and the resulting equations articulate the balance of momentum due to pressures and stresses within the fluid.
Examples & Analogies
Think of a car accelerating on a highway. The push of the engine (force) acts on the mass of the car resulting in acceleration. Similarly, when analyzing fluids, we consider how forces (pressure, gravity, viscous forces) affect the fluid's motion (acceleration) to arrive at the Navier-Stokes equations.
Handling Complexities: Assumptions and Simplifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you consider it that I have this big control volumes which is movable control volume okay it is moving it.
Detailed Explanation
In this section, the derivation of the Navier-Stokes equations is simplified under specific assumptions, such as considering incompressible and isothermal flow conditions. These assumptions help reduce the complexity of the governing equations, making them easier to solve by focusing on how density and viscosity behave under steady conditions.
Examples & Analogies
Think of a kitchen sponge soaked with water. If you squeeze it gently, the water (fluid) flows out without changing density significantly. This scenario mimics incompressible flow conditions, allowing us to employ simplified versions of fluid equations like the Navier-Stokes under certain assumptions.
Exploring the Navier-Stokes Equation Outputs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we have a four equations and four unknowns. So, we can solve it but still it has the problems is comes it here is it is a unsteady time component is there nonlinear partial differential equations.
Detailed Explanation
The final expressions of the Navier-Stokes equations yield four equations with four unknowns—pressure and the three velocity components. However, due to the inherent nonlinearities and the time dependence of these equations, obtaining exact solutions can be problematic and often requires numerical methods or approximations.
Examples & Analogies
Imagine trying to predict the exact motion of a crowded bus stop where people are constantly moving in and out. Just like analyzing complex flow behaviors requires sophisticated simulations, understanding fluid dynamics through the Navier-Stokes equations often involves approximations and computational models to handle the complexities.
Application of Navier-Stokes Equations in Real Situations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at this the equations what we have in Kaji's equations we have a stress tensors okay which is having 9 components.
Detailed Explanation
In practical terms, the equations derived from Cauchy's principles incorporate stress tensors with components that must be modeled to account for real-world fluid behaviors. When dealing with multiple forces acting on a fluid, it's essential to know how these stress components interrelate to accurately predict the fluid's motion and time evolution.
Examples & Analogies
Think about the water flowing through a pipe with different bends and fittings. Each bend can introduce changes in the pressure and velocity of the fluid, akin to how stress components influence the flow in real-world situations. Engineers must consider these variables when designing systems that manage fluid movement effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Historical Context: The contributions of Navier and Stokes, explaining how they independently derived the equations, which has led to modern fluid dynamics.
-
Basic Definitions: Understanding Newtonian vs. non-Newtonian fluids and the conditions under which the Navier-Stokes equations are applied, focusing on incompressible, isothermal flows.
-
Mathematical Derivations: Begin with Cauchy’s equations in vector form, detailing mass and momentum conservation principles through control volumes, and expanding definitions to incorporate stress tensors.
-
Assumptions and Simplifications: Highlighting the approximations made to reduce complexity, including assumptions of rest for fluids leading to shear stress considerations.
-
Equations in Different Coordinate Systems: Introduction to Cartesian and cylindrical coordinates and how the equations transform accordingly. The emphasis on the interrelationship between velocity, pressure, and density fields.
-
Through this examination, the significance of understanding these equations and their derived forms are clear, as they form the backbone of fluid mechanics and computational fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Navier-Stokes equations are crucial for simulating blood flow in arteries.
-
Meteorologists use these equations to predict weather patterns by modeling the atmosphere.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids dense, they glide with ease; Navier and Stokes, do as they please.
📖 Fascinating Stories
-
Once upon a time, two brilliant men, Navier and Stokes, discovered equations that helped predict how water flows in rivers and skies.
🧠 Other Memory Gems
-
Use 'NICE' to remember the assumptions: Newtonian, Incompressible, Constant temperature, and Equal pressure.
🎯 Super Acronyms
NSE = Navier-Stokes Equations for fluid Dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations describing the motion of viscous fluid substances.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows used for applying fluid dynamics equations.
-
Term: Newtonian Fluid
Definition:
Fluids that have a constant viscosity and follow a linear relationship between shear stress and shear strain.
-
Term: NonNewtonian Fluid
Definition:
Fluids that do not have a constant viscosity and display a nonlinear relationship between shear stress and shear strain.
-
Term: Incompressible Flow
Definition:
A flow where the fluid density remains constant.
-
Term: Isothermal Flow
Definition:
A flow where the fluid temperature remains constant.