Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Navier-Stokes Equations
Unlock Audio Lesson
Good morning everyone! Today, we begin discussing the Navier-Stokes equations, which are crucial in fluid dynamics. Can anyone tell me who contributed to the equations?
Was it Claude-Louis Navier and George Stokes?
Exactly! They derived these equations independently over 200 years ago. This foundation allows us to solve complex fluid flow problems. Now, can anyone explain why we need these equations?
Because they help us understand how fluids move?
Correct! They define the motion of fluids under various forces and stresses.
Basic Derivations of the Navier-Stokes Equations
Unlock Audio Lesson
Let's dive into the derivations. We start from Cauchy's equations, which are derived from Newton’s second law. What do we know about Newton's second law?
Force equals mass times acceleration!
Exactly! In fluid dynamics, we apply it to control volumes. For example, can anyone derive the form of the force acting on a fluid element?
We can consider the body forces and surface forces, right?
That's right! And when the forces balance, we get the Navier-Stokes equations. Remember, these equations describe internal forces as well as the external forces acting on the fluid. It's all connected!
Discussing the Assumptions: Incompressible and Isothermal Flow
Unlock Audio Lesson
Now, let’s talk about the assumptions we make for deriving the Navier-Stokes equations, particularly incompressible and isothermal flow. What do these mean?
Incompressible means the density of the fluid remains constant.
And isothermal means that the temperature doesn't change significantly in the flow.
Exactly! These assumptions greatly simplify the mathematics involved. Can anyone think of fluid systems where these assumptions might not hold?
Well, in high-speed flows, compressibility can be significant, right?
Great point! Recognizing where these assumptions apply helps in accurately modeling fluid behavior.
Applications of Navier-Stokes Equations in Coordinate Systems
Unlock Audio Lesson
After discussing the derivations and assumptions, let’s look at how we apply the Navier-Stokes equations in different coordinate systems. Who can explain how we might approach this in Cartesian coordinates?
We use the x, y, and z directions to define the flow and calculate forces?
Yes! And what about cylindrical coordinates? How does that change our approach?
We would use radius, angle, and height instead!
Exactly! Each coordinate system has unique advantages depending on the fluid problem being analyzed. Can anyone think of a fluid flow scenario that might benefit from cylindrical coordinates?
Like fluid flow in pipes or cylindrical tanks?
Perfect! Acknowledging the appropriate coordinate system enhances our model's accuracy!
Challenges in Solving the Navier-Stokes Equations
Unlock Audio Lesson
Lastly, let’s discuss the challenges in solving the Navier-Stokes equations. Why are they considered complex?
Because they are nonlinear partial differential equations!
And accounting for time and space makes it even harder!
Exactly! These complexities lead us to approximate solutions rather than exact ones. Why do you think this drives the development of Computational Fluid Dynamics?
Because it allows us to simulate fluid behavior without solving equations analytically!
Absolutely right! We use computational methods to analyze fluid motion when analytical solutions aren’t feasible. Great job today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Navier-Stokes equations form the foundation of fluid mechanics, essential for solving various fluid flow problems. This section discusses their derivations, assumptions about fluid behavior, and the application in both Cartesian and cylindrical coordinate systems.
Detailed
The Navier-Stokes equations are pivotal in understanding fluid dynamics, derived independently by Claude-Louis Navier and George Stokes. This section details the equations' derivation under the assumptions of incompressible and isothermal flow, using both Cartesian and cylindrical coordinate systems. The discussions emphasize vector notations, the role of stress tensors, and the impact of shear and body forces, ultimately simplifying complex fluid models into manageable equations. It also addresses the underlying physics connecting these equations to Newton's laws, while presenting the challenges associated with solving the nonlinear partial differential equations they represent.
Youtube Videos
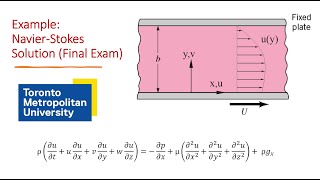
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Navier-Stokes equations form the basic foundations of computational fluid dynamics and are applicable to many complex fluid flow problems. These equations were derived independently by Claude-Louis Navier, a French physicist, and George Stokes, an English mathematician. They cross-verified their results, leading to the equations we study today.
Detailed Explanation
The Navier-Stokes equations describe how fluids (gases and liquids) move. Understanding them is crucial because they help solve problems related to fluid dynamics, including weather patterns, ocean currents, and airflow around aircraft. The equations were developed by two scientists over 200 years ago, and they provide a mathematical model that can predict fluid motion by detailing the influence of forces like pressure, viscosity, and gravity.
Examples & Analogies
Think of a busy highway where cars flow smoothly if they all follow the rules. The Navier-Stokes equations are like the traffic rules for fluid flow, helping predict how the fluid (like cars) will move under different conditions.
Key Concepts: Newtonian and Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, we distinguish between Newtonian and non-Newtonian fluids. Newtonian fluids have a constant viscosity that does not change with the rate of deformation, while non-Newtonian fluids have a viscosity that can vary with the deformation rate.
Detailed Explanation
For Newtonian fluids like water or air, the relationship between shear stress and shear rate is linear, meaning if you increase the force, the flow speed will also increase proportionately. In contrast, non-Newtonian fluids, such as ketchup or blood, may become thicker or thinner depending on how fast they are stirred. This difference in behavior is critical in calculating fluid motion using the Navier-Stokes equations.
Examples & Analogies
Imagine trying to pour honey versus water. Honey flows much slower than water, and if you try to stir it fast, it might become even thicker. This illustrates how non-Newtonian fluids behave differently from Newtonian fluids.
Deriving the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Navier-Stokes equations account for incompressible isothermal flow and are derived from the conservation of mass (continuity) and the laws of motion (Newton's laws). They include terms representing forces due to pressure, viscosity, and external fields like gravity.
Detailed Explanation
The derivation involves starting from fundamental principles such as conservation of mass and applying them to a small control volume of fluid. The equations are nonlinear because they involve terms from both the velocity field and the stresses within the fluid. This complexity often makes finding exact solutions challenging, except in simplified cases.
Examples & Analogies
Consider a small balloon filled with water. If you squeeze the balloon, different pressures are exerted on different parts of the balloon due to your squeeze. The Navier-Stokes equations help explain how the water moves and changes shape in response to those pressures.
Applications and Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Due to the complexity of the Navier-Stokes equations, finding exact solutions is often not possible. This has led to the development of Computational Fluid Dynamics (CFD), a field that uses numerical analysis and algorithms to approximate solutions for fluid flow problems.
Detailed Explanation
CFD allows engineers and scientists to simulate fluid flow in various scenarios, including airflow over wings, water flowing in pipes, or forecasting weather patterns. By using computers to solve the Navier-Stokes equations numerically, researchers can model real-world behaviors without needing simple analytical solutions.
Examples & Analogies
Think of a weather forecast. Meteorologists use computers to simulate the atmosphere and predict how air will move based on various factors. This 'simulation' is similar to what CFD does for fluid dynamics, providing a way to visualize and understand complex flows.
The Challenges of Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Navier-Stokes equations are recognized as challenging because they are nonlinear and can lead to chaotic behavior in certain conditions. Understanding their solutions is still an area of active research in mathematics and physics.
Detailed Explanation
Nonlinear equations like the Navier-Stokes equations can produce complex solutions that are sensitive to initial conditions, making predictions difficult. This is why understanding the behavior of different fluids is essential in engineering and environmental studies.
Examples & Analogies
Imagine trying to balance on a tightrope while a storm is blowing and the wind changes rapidly. Just as it's hard to predict your movement in that chaotic situation, the same goes for fluids modeled by the Navier-Stokes equations as they can behave unpredictably under certain conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Essential for modeling fluid flow under various conditions.
-
Incompressible Flow: A simplified flow condition assuming constant density.
-
Isothermal Flow: Assumes temperature uniformity in the fluid.
-
Stress Tensor: Describes forces within a deformable body or fluid.
-
Control Volume: A particular volume in space for fluid dynamics analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing the flow in a pipe using the Navier-Stokes equations allows engineers to predict pressure drops.
-
Modeling the airflow over an airplane wing using computational fluid dynamics based on Navier-Stokes equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow without a change in mass, the Navier-Stokes will help you pass!
📖 Fascinating Stories
-
Once in a kingdom, there were two wizards named Navier and Stokes. They held the secrets of fluid magic in two separate tomes, bringing harmony to the rivers and streams. With their equations, they helped many a fisherman cast their nets with ease.
🧠 Other Memory Gems
-
I.S. Incompressible & Isothermal: Remember 'I.S.' for the two main assumptions in Navier-Stokes.
🎯 Super Acronyms
F.L.O.W. - Forces, Limits, Operations of Water - Summarizing what Navier-Stokes governs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations governing the motion of fluid substances.
-
Term: Incompressible Flow
Definition:
Fluid flow with a constant density across the flow field.
-
Term: Isothermal Flow
Definition:
Flow in which the temperature remains constant throughout the fluid.
-
Term: Stress Tensor
Definition:
A mathematical representation that describes the internal forces acting within a fluid.
-
Term: Control Volume
Definition:
A defined region in space through which fluid may flow, used for analyzing fluid motion.