Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Today, we'll explore the Navier-Stokes equations, critical for understanding fluid dynamics. Who can tell me why they are important?
They help us describe how fluids move.
Exactly! These equations consider various forces acting on fluids. Can anyone name some forces?
Body forces like gravity and surface forces due to viscosity.
Spot on! Remember: body forces act throughout the volume, while surface forces act at the boundaries. Let's remember these as *'BS Forces'* for 'Body-Surface'.
What about non-Newtonian fluids? Are they included in Navier-Stokes equations?
Good question! The standard Navier-Stokes equations assume Newtonian fluids. However, we need modifications for non-Newtonian fluids that behave differently.
In summary, Navier-Stokes governs fluid flow by including forces acting on the fluid. Next time, we'll delve into their derivation!
Deriving the Navier-Stokes Equations
Unlock Audio Lesson
Let's derive the Navier-Stokes equations! Who can remind me what assumptions we make?
We assume incompressible, isothermal flow!
Exactly. What does 'incompressible' mean in fluid terms?
It means density remains constant.
Right! Density being constant simplifies our equations during derivation. Now, can someone show me how we include surface and body forces?
We write them in our force balance equations.
Exactly! In our force balance, we have terms for pressure, gravity, and viscosity. Let's think of forces in terms of *'P-G-V'*.
To summarize, we've derived the equations based on our flow assumptions, emphasizing the role of pressure and viscous stresses.
Challenges in Fluid Dynamics
Unlock Audio Lesson
Now that we know the Navier-Stokes equations, what are some challenges we face?
They can be really complex and sometimes impossible to solve directly!
Very true! Nonlinearity and the number of variables can create difficulties. That's why we often use approximation techniques or computational methods.
What’s CFD?
CFD stands for Computational Fluid Dynamics. It's a powerful tool for simulating fluid flow, allowing us to tackle problems where analytical solutions are hard to find.
So in summary, the complexities of fluid dynamics often lead us to utilize computational methods to find practical solutions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the derivation and implications of the Navier-Stokes equations, highlighting the roles of body forces, surface forces, and the various assumptions of the flow conditions. Key distinctions between Newtonian and non-Newtonian fluids are made, along with an analysis of the complexities of solving these equations under different coordinate systems.
Detailed
Detailed Summary
The section provides a comprehensive exploration of Navier-Stokes equations, which are vital in the field of fluid mechanics for comprehensively analyzing fluid flow phenomena. It begins with historical context, attributing the development of these equations to Claude-Louis Navier and George Stokes, who developed them independently.
Key Points:
- Fluid Types: The distinctions between Newtonian and non-Newtonian fluids are discussed, underlining that Newtonian fluids maintain a linear relationship between shear stress and shear strain rate, relevant in many standard fluids like water, while non-Newtonian fluids exhibit varying behaviors depending on stress and strain rate.
- Forces in Fluid Flow: Two principal forces affecting fluid flow are emphasized: body forces (e.g., gravity) and surface forces (e.g., viscous stress). The section elaborates on how these forces are captured through the equations that govern fluid motion.
- Equations: The Navier-Stokes equations are derived for incompressible and isothermal flows, illustrating how these classical equations can be expanded to analyze the dynamics of fluids in different coordinate systems and under diverse conditions.
- Complexity of Solutions: The challenges of finding analytical solutions to these equations are acknowledged, especially for practical applications. Various approximations and numerical methods, including Computational Fluid Dynamics (CFD), are necessary to tackle real-world fluid flow issues.
Understanding these concepts is fundamental in fields that require fluid dynamics analysis, from engineering disciplines to environmental studies.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Forces in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
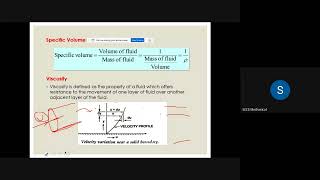
In fluid mechanics, when analyzing fluid dynamics, it is essential to consider the respective forces acting on a fluid element. The two major types of forces are body forces and surface forces. Body forces arise from the mass of the fluid under the influence of gravity, whereas surface forces result from the interactions at the boundary of fluid elements, such as shear stress due to fluid motion.
Detailed Explanation
In fluid dynamics, it's crucial to understand the types of forces that act on fluids. Body forces include forces like gravity that act throughout the volume of the fluid. For example, when water flows down a river, gravity pulls it towards the ground continuously. On the other hand, surface forces occur at the boundaries of fluid elements, like the friction that occurs when fluid flows over a surface. Shear stress is a common example of a surface force, where different layers of fluid move relative to each other, creating friction.
Examples & Analogies
Think of a bowl of honey. As you tilt the bowl, gravity (a body force) pulls the honey downward, while the honey also experiences resistance against the sides of the bowl (a surface force). This interaction illustrates how both body and surface forces influence fluid behavior.
Newton's Second Law in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The fundamental principle governing the dynamics of fluids is Newton's second law, expressed as force equals mass times acceleration. In fluid dynamics, this can be extended to include elements such as the volume of control, body forces, and surface forces acting on infinitesimally small control volumes.
Detailed Explanation
Newton's second law states that the force acting on an object equals its mass times acceleration (F=ma). In fluid dynamics, we apply this law to small portions of fluids called control volumes. Here, the acceleration of a fluid element results not just from its mass but also from forces acting on it, including gravity (a body force) and shear stress at the boundary (a surface force). This means we can study how these forces change the motion of fluids across different conditions over time.
Examples & Analogies
Imagine pouring a syrupy liquid onto a plate. The syrup flows slower than water because of viscosity (the internal friction of fluid). According to Newton's second law, the forces acting on the syrup particles (like gravity and resistance from the plate) affect their acceleration and flow rate.
Understanding Continuity and Acceleration in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In discussing the flow characteristics of fluids, it’s essential to address both local and convective accelerations. Local acceleration refers to changes in velocity within a control volume as conditions change over time, while convective acceleration is related to the changes in velocity experienced as the fluid moves through the control volume itself.
Detailed Explanation
When we analyze fluid flow, we must consider how the speed of the fluid changes over time and space. Local acceleration occurs if the speed of the fluid changes while it occupies the same position in space. Conversely, convective acceleration happens when the fluid moves into areas with different speeds or directions. For instance, consider water flowing from a wide area into a narrow stream; the fluid speed increases due to the decrease in the cross-sectional area, showing convective acceleration.
Examples & Analogies
Imagine a river that narrows at a section. The water flows faster through the narrow part, showing how fluid acceleration can occur not only from changes over time but also from the shape of its path. Like running faster when you exit a wide hallway into a narrow one.
Force Balance in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Effective fluid motion results from balancing the various forces acting on the fluid element. The relation between the forces due to the pressure gradients, gravitational effects, and viscous stresses is crucial for understanding complex fluid behaviors.
Detailed Explanation
In fluid mechanics, understanding how forces interact and balance each other helps predict how fluids will behave. For example, in a pipe, the pressure difference between the entrance and exit creates a net force that propels fluid forward. Gravitational force acts downward, while shear stress influences the flow at the boundaries. By analyzing these forces, we can understand the dynamics of fluid systems.
Examples & Analogies
Think of water flowing down a slide. The force of gravity pulls it down, but the shape of the slide and friction (viscous stress) slow it down somewhat. The balance between these forces determines how quickly the water reaches the bottom.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations that describe fluid flow dynamics under various forces.
-
Body Forces vs. Surface Forces: Understanding the differences between forces that act throughout the volume of a fluid and those that act at the fluid's boundaries.
-
Newtonian vs. Non-Newtonian Fluids: Differentiating fluids with constant viscosity from those whose viscosity changes with flow conditions.
-
Incompressible and Isothermal Flow: Conditions where density remains constant and temperature does not fluctuate significantly.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing in a pipe is an example of a Newtonian fluid where the Navier-Stokes equations can be applied.
-
Blood flow, which may exhibit non-Newtonian characteristics, poses a challenge to the direct application of these equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids we have forces of two kinds, Body and Surface, it’s not hard to find!
📖 Fascinating Stories
-
Imagine a fluid trying to flow down a river. Gravity pulls it down while it also faces resistance from the riverbanks, illustrating body and surface forces.
🧠 Other Memory Gems
-
Remember 'B-S' for Body-Surface forces when discussing forces in fluid dynamics.
🎯 Super Acronyms
Use 'IN-ISO' to remember Incompressible and Isothermal when deriving Navier-Stokes equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes equations
Definition:
Equations that describe the motion of viscous fluid substances.
-
Term: Body Forces
Definition:
Forces that act throughout the volume of a fluid, such as gravitational force.
-
Term: Surface Forces
Definition:
Forces that act at the interface between the fluid and its boundaries.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density is constant despite pressure changes.
-
Term: Isothermal Flow
Definition:
Flow where the temperature remains constant throughout the fluid's motion.
-
Term: Newtonian Fluids
Definition:
Fluids with a linear relationship between shear stress and strain rate.
-
Term: NonNewtonian Fluids
Definition:
Fluids whose viscosity can change with the shear rate.
-
Term: Computational Fluid Dynamics (CFD)
Definition:
A branch of fluid mechanics that uses numerical analysis and algorithms to solve fluid flow problems.