Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Good morning everyone! Today, we will explore the Navier-Stokes equations, a cornerstone of fluid mechanics, significant for computational fluid dynamics. Can anyone tell me who derived these equations?
Was it Navier and Stokes?
That's correct! Navier, a French physicist, and Stokes, an English mathematician, both derived them in the 19th century. Their equations describe how fluids behave under various conditions. Why do you think understanding these equations is essential, especially for engineers?
I think it helps us solve real-world fluid problems like weather patterns or engineering designs.
Exactly! The equations model fluid flow and can apply to both Newtonian fluids like water and non-Newtonian fluids like blood or slurries. Let's remember the acronym 'NFS' for Navier, Fluid, and Stokes!
Key Assumptions in Navier-Stokes Equations
Unlock Audio Lesson
As we study the Navier-Stokes equations, it's important to understand the assumptions we make. Can anyone name one?
I think we often assume incompressible flow?
Correct! In incompressible flow, the fluid's density remains constant. We also assume isothermal conditions, meaning the temperature doesn't change significantly within the fluid. Together, these simplify our equations. Can anyone explain why simplifying assumptions are useful?
It helps us model complex systems more efficiently!
Right! Remember the mnemonic 'I IS' to remind us: Incompressible and Isothermal conditions simplify our calculations!
Understanding Fluid Dynamics
Unlock Audio Lesson
Now, let's talk about Newtonian and non-Newtonian fluids. What do we mean when we call a fluid Newtonian?
These are fluids where the shear stress is directly proportional to the shear strain rate, right?
Exactly! Water is a classic example. Non-Newtonian fluids, however, behave differently. Can someone give an example of a non-Newtonian fluid?
Like ketchup! It doesn't flow until you apply pressure.
Very good! Let’s remember ‘Ketchup Changes’ to signify Non-Newtonian properties can change with applied stress!
Applications of Navier-Stokes Equations
Unlock Audio Lesson
Today, we will explore how these equations apply to real-life scenarios. Could anyone think of a specific application?
Maybe in weather forecasting or predicting ocean currents?
Absolutely! The Navier-Stokes equations help in modeling how air and water flow under various conditions. Understanding boundary conditions is vital here. Can anyone explain why boundary conditions are critical?
They define how fluid behaves at the surfaces it interacts with.
Exactly! To remember this, think 'BC=Surface Behavior'! Boundary Conditions are essential for accurate predictions!
Examining Challenges in Fluid Dynamics
Unlock Audio Lesson
We've learned about the complexity of the Navier-Stokes equations. What challenges do we face when solving them?
They are nonlinear differential equations, making them tough to solve analytically?
That's right! This is why we often resort to computational fluid dynamics for solutions. Can anyone explain its significance?
It allows us to model fluid behaviors that are otherwise too complex to solve!
Exactly! Keep in mind, ‘NLP = Toughness’ to remember: Nonlinear, Challenging, Practical! This summarizes the challenges with analytic solutions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the Navier-Stokes equations as critical elements in computational fluid dynamics, highlighting the historical context of their derivation by Navier and Stokes. It presents key concepts such as Newtonian and non-Newtonian fluids, the assumptions made in deriving the equations, and their applications in fluid flow problems.
Detailed
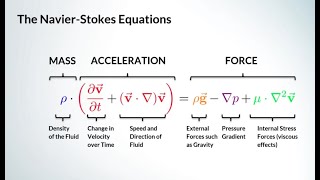
The Navier-Stokes equations form the backbone of fluid mechanics, derived independently by Claude-Louis Navier and George Stokes. They are essential for understanding complex fluid flow dynamics. This section delves into the derivation process of the Navier-Stokes equations, emphasizing assumptions for incompressible and isothermal flow to simplify the equations. It also introduces the importance of coordinate systems, such as Cartesian and cylindrical, and offers insights into boundary conditions relevant for solving practical fluid flow cases. Throughout the discussion, the relationship between stress tensors and fluid dynamics is examined, along with the distinction between Newtonian and non-Newtonian fluids, underscoring the relevance of fluid viscosity in flow behavior. The section ultimately illustrates that the Navier-Stokes equations can simplify the modeling of fluid mechanics, although finding exact solutions remains a challenge and often requires computational fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning all of you. Today we are going to discuss very interesting topics, the topics on Navier-Stokes equations. That is what the basic foundations of computational fluid dynamics and many of the complex fluid flow problems also we can solve it by using Navier-Stokes equations.
Detailed Explanation
The Navier-Stokes equations are critical in fluid mechanics, as they describe how fluids move. They serve as the foundation for computational fluid dynamics (CFD), which is the use of numerical methods to analyze fluid flows. Understanding these equations allows us to model and solve complex fluid flow problems effectively.
Examples & Analogies
Think of the Navier-Stokes equations as the set of rules that govern how water flows in a river. Just as you can use these rules to predict where the water will go, engineers use the equations to predict how fluids will behave in various conditions.
Historical Background
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it for vector notation and related to the vectors, operations in fluid mechanics, the best course which is available in MIT OpenCourseWare which on fluid mechanics you can get it and also we are going through this F.M. White book on fluid mechanics. These are 3 books, you can always refer it to understand this Navier-Stokes equations part. Now, if you look go through its who is Navier and who is Stokes okay the way back the French physicist okay Claude-Louis Navier okay so it is almost 200 years back and also this George Stokes from as a mathematicians from England both have derived the Navier-Stokes equations independently.
Detailed Explanation
The Navier-Stokes equations were derived independently by Claude-Louis Navier and George Stokes in the early 19th century. Navier, a French physicist, contributed to the understanding of fluid flow behavior, while Stokes, a British mathematician, worked on the mathematical formulation. Their contributions have become fundamental to studying fluid dynamics today.
Examples & Analogies
Imagine two inventors working on a similar invention in different parts of the world. Even without communication, they both arrive at the same groundbreaking idea, just like Navier and Stokes did with their equations. Their combined legacy impacts fields like weather forecasting, aircraft design, and even ocean currents.
Deriving Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I will talk about the derivations of Navier-Stokes equations with assumptions of incompressible isothermal flow.
Detailed Explanation
Derivations of the Navier-Stokes equations typically start with fundamental principles of mass, momentum, and energy conservation. Key assumptions include incompressibility (constant density) and isothermal flow (constant temperature). These assumptions simplify the equations, making them more manageable and relevant for many practical applications.
Examples & Analogies
Consider a hot air balloon. If the air inside the balloon is heated, it becomes less dense, and the balloon rises. This situation illustrates compressible flow. However, if the balloon was filled with water instead, which is incompressible, the analysis would be simpler, akin to how the Navier-Stokes equations are derived under the assumption of incompressibility.
Velocity Divergence and Physical Interpretations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the the vectors divergence okay. If you look at that del and V the velocity divergence it is talking about the net volume outflow from a control volume.
Detailed Explanation
Velocity divergence refers to how much fluid is expanding or contracting at a point. If it’s positive, more fluid is exiting a volume than entering, indicating a flow source. Conversely, if it’s negative, fluid is accumulating, indicating a sink.
Examples & Analogies
Imagine a sponge absorbing water; as the sponge soaks up water (negative divergence), it expands. On the other hand, if you squeeze a sponge, the water flows out (positive divergence). This analogy helps illustrate how divergence informs us about fluid flow behavior in different scenarios.
Cauchy's Equations and Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the Cauchy's equations, we are deriving the basic equations for linear momentum equations for control volumes which is having infinitely small control volumes.
Detailed Explanation
Cauchy’s equations describe the motion of fluids through momentum conservation principles. They consider forces acting on an infinitesimal control volume of fluid. Body forces (like gravity) and surface forces (like pressure) are analyzed to understand how fluids behave under different conditions.
Examples & Analogies
Think of a water bottle sitting on a scale. The scale reads the weight of the water (body force) plus the pressure at the bottom of the bottle (surface force). Both forces contribute to the total force the scale measures, similar to how surface and body forces contribute to fluid movement.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Also, I will talk about revisit Newtonian fluid and non-Newtonian fluid part which is quite interesting to look at how we can use for this Navier-Stokes equations.
Detailed Explanation
Newtonian fluids exhibit a linear relationship between shear stress and shear rate, meaning they flow predictably (like water). Non-Newtonian fluids do not have this predictable behavior; their flow characteristics change under different conditions (like ketchup). Understanding this distinction is critical in applying the Navier-Stokes equations correctly.
Examples & Analogies
Consider stirring honey versus water. Honey flows much differently and requires more effort to move; it behaves non-Newtonian where its viscosity can change with the applied force. This analogy serves to understand how fluid properties affect their behavior in different conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Derivation of the Navier-Stokes Equations: Explains the mathematical framework behind fluid behavior.
-
Importance of Incompressibility: Highlights the significance of assuming constant density in fluid flow.
-
Newtonian vs Non-Newtonian Fluids: Distinguishes between fluids that follow Newton's law of viscosity and those that do not.
-
Boundary Conditions: Discusses the critical role of boundary conditions in solving fluid flow problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Navier-Stokes equations are used to model airflow over the wings of an aircraft, helping to optimize designs for better performance.
-
In biomedical engineering, the equations can be applied to predict blood flow dynamics in arteries, aiding in the design of medical devices.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow, to go with ease, remember NFS: Navier, Fluid, Stokes, please!
📖 Fascinating Stories
-
Imagine a river flowing steadily; its consistency is like water, a Newtonian friend, while ketchup, thick and sticky, teaches us about non-Newtonian ends.
🧠 Other Memory Gems
-
I IS: Recall Incompressible and Isothermal to ease your fluid problems.
🎯 Super Acronyms
Ketchup Changes
- to remember Non-Newtonian Fluid behaviors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations that describe the motion of fluid substances.
-
Term: Newtonian Fluid
Definition:
Fluids that have a constant viscosity and follow Newton's law of viscosity.
-
Term: NonNewtonian Fluid
Definition:
Fluids that do not have a constant viscosity and display varying behavior under different shear rates.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density is constant.
-
Term: Isothermal Conditions
Definition:
Conditions in which temperature remains constant throughout the fluid.
-
Term: Stress Tensor
Definition:
A mathematical description of the internal distribution of forces within a deformable body.
-
Term: Boundary Conditions
Definition:
Constraints that define the behavior of fluid at the physical boundaries of a system.