Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Vector Notations
Unlock Audio Lesson
Today, we're going to explore vector notations crucial for fluid mechanics. Can anyone tell me how vectors are used in physical scenarios?
Vectors help to represent quantities like velocity and force, right?
Exactly! Vectors not only provide direction but also magnitude, which is vital in fluid dynamics. For instance, the velocity vector indicates both the speed and direction of the flow.
What about the vector operations like divergence? How does that relate to fluid flow?
Great question! Divergence measures the net flow out of a control volume. If the divergence of velocity is positive, it indicates a source, while a negative divergence indicates a sink.
Can you give us a mnemonic to remember vector operations?
Sure! Remember 'D-G-C' for Divergence, Gradient, and Curl — that way, you can recall the three key vector operations we use in fluid mechanics!
To summarize, vectors are essential in fluid mechanics to define motion, and understanding vector operations helps us analyze fluid flows effectively.
Dimensional Analysis
Unlock Audio Lesson
Today, let's discuss dimensional analysis and its importance in validating fluid equations. Why do you think this is crucial?
It's important to ensure our equations are dimensionally consistent!
Exactly! For instance, in the Navier-Stokes equations, every term must have consistent units. Can you think of what units are involved?
Mass, length, and time are the fundamental dimensions we need to consider.
Correct! If we have a mass term, we need to analyze its units against acceleration, which involves lengths and time. This helps avoid errors in calculations.
Is there a specific way to go about dimensional analysis?
Yes, start with the fundamental dimensions: M for mass, L for length, and T for time. Then, break down every term in your equations and see if they align.
To summarize, dimensional analysis allows us to check for consistency in our equations, ensuring accurate physical modeling without dimensional discrepancies.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Lesson
Now, let's delve into the differences between Newtonian and non-Newtonian fluids. What distinguishes these two categories?
Newtonian fluids have a constant viscosity regardless of the stress applied, while non-Newtonian fluids change their viscosity under stress.
Spot on! For example, water is a Newtonian fluid, while ketchup is a non-Newtonian fluid. Can anyone explain why temperature can affect viscosity?
Temperature changes can affect molecular interactions in the fluid, thus affecting its flow behavior.
Exactly! As temperature increases, many fluids become less viscous. This knowledge is vital when applying the Navier-Stokes equations, as they primarily apply to Newtonian fluids.
Can we classify other fluids like blood?
Yes! Blood is classified as a non-Newtonian fluid since its viscosity changes with shear rate. To recap, your understanding of fluid properties like viscosity helps us apply fundamental principles correctly.
Application of Navier-Stokes Equations
Unlock Audio Lesson
Having understood vector notations, let’s discuss how they play a role in deriving the Navier-Stokes equations. Who can tell me what the Navier-Stokes equations represent?
They represent the conservation of momentum in fluid motion.
Correct! These equations are essential for modeling the dynamics of fluid flow. Can someone outline the terms involved in the basic formulation?
There are terms for local acceleration, convective acceleration, pressure gradient, and viscous forces.
Good job! Let's break these down a bit. Local acceleration correlates to unsteady flow, while convective acceleration is tied to fluid's motion. How about we explore how we can streamline these components?
Using assumptions like incompressible flow helps simplify the equations.
Exactly! Incompressible and isothermal assumptions allow us to derive more manageable forms of these equations, making real-world fluid flow problems easier to solve. In summary, understanding vector notations aids in comprehending the behavior and equations governing fluid motion.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
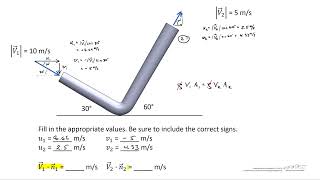
In this section, we explore vector notations and their applications in fluid mechanics, specifically relating them to the Navier-Stokes equations. The emphasis is on understanding vector operations, dimensions of physical quantities, derivations related to momentum equations, and differentiating between Newtonian and non-Newtonian fluids.
Detailed
Vector Notations and Dimensions
This section delves into the crucial role of vector notations and dimensional analysis within the context of fluid mechanics. Vector notation is essential for expressing complex fluid motions and utilizing equations like the Navier-Stokes equations. The exploration begins with defining vector operations such as divergence, gradient, and curl, highlighting their significance in the study of fluid dynamics.
Key Points:
- Vector Notation in Fluid Mechanics: Vectors represent quantities such as velocity, acceleration, and force in fluid motion.
- Divergence and Continuity:
- The divergence of velocity indicates the net outflow of volume from a control volume.
- The continuity equation reflects the conservation of mass in fluids.
- Momentum Equations: The Navier-Stokes equations are derived from Newton's laws, focusing on momentum conservation in fluid mechanics.
- Newtonian vs Non-Newtonian Fluids: Understanding the differences in stress-strain behavior and the implications for fluid dynamics.
- Dimensional Analysis: Evaluating the dimensions of various physical quantities helps validate the equations derived from fundamental principles.
This knowledge is foundational for advancing to more complex topics in fluid mechanics.
Youtube Videos
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Vector Notations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look go through its who is Navier and who is Stokes okay the way back the French physicist okay Claude-Louis Navier okay so it is almost 200 years back and also this George Stokes from as a mathematicians from England both have derived the Navier-Stokes equations independently.
Detailed Explanation
This chunk provides a brief historical context for the Navier-Stokes equations, mentioning their derivation by Claude-Louis Navier and George Stokes over 200 years ago. Navier was a physicist, while Stokes was a mathematician, and together they contributed significantly to fluid mechanics by formulating these equations that describe the motion of viscous fluid substances.
Examples & Analogies
Think of the Navier-Stokes equations like the foundational laws of physics for fluids, similar to how Newton's laws of motion are foundational for all physical movements. Just as we rely on Newtonian physics to describe how solid objects behave, engineers and scientists use Navier-Stokes equations to predict how fluids like water and air will flow.
Understanding Vectors in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In vector form if you remember it which is the linear momentum equations deriving with the components like rho by rho t rho v is velocity plus is equal to del dot product of rho v is equal to rho g is a vectors plus we have the del product or divergence of the stress tensor.
Detailed Explanation
This segment introduces the concept of vectors in fluid mechanics, specifying how linear momentum is expressed using equations that incorporate density (rho), velocity (v), and acceleration due to gravity (g). It talks about the divergence of the stress tensor indicating how forces within a fluid interact and lead to its flow. This part emphasizes the significance of vector notation in representing fluid behavior mathematically.
Examples & Analogies
Consider a crowd of people moving through a narrow door. The density of the crowd, their speed, and the resulting pushes from different directions can be understood as vectors. Just like a sports team passing a ball based on each player's position and speed, fluid mechanics uses vectors to determine how different properties like pressure and velocity impact fluid flow.
Velocity Divergence and Its Implications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the vectors divergence okay. If you look at that del and V the velocity divergence is talking about the net volume outflow from a control volume.
Detailed Explanation
Velocity divergence provides insights into how fluid expands or contracts in a control volume. When we talk about the divergence of a velocity vector field, we are essentially measuring the rate at which fluid is flowing out of a point relative to the amount entering it. In a physical sense, if the divergence is positive, more fluid exits than enters, leading to a 'source' in the flow field; if it's negative, we have a 'sink.'
Examples & Analogies
Imagine a balloon being inflated. As air is pumped into the balloon, the volume inside increases, which corresponds to a negative divergence at the inflating point. Conversely, if you have a punctured balloon, air rushes out, representing a positive divergence. This behavior helps us analyze weather patterns or river flows, where areas of high and low pressure cause air or water to accumulate or disperse.
Understanding Mass Outflow with Density and Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same way if I just put it the del into rho into v what is this is indicating is the mass outflow for a unit control volume that is what is indicating me.
Detailed Explanation
This chunk explains how mass outflow can be expressed mathematically. By multiplying the density of a fluid by its velocity and applying the divergence operator, we can calculate the mass flow rate in a control volume, which is critical for understanding how fluid moves in various systems. This relationship is foundational in fluid mechanics, linking density, velocity, and flow rates.
Examples & Analogies
Think of a fire hose spraying water. The amount of water coming out of the hose at any point in time depends on how fast the water is moving (velocity) and how dense the water is (which is typically constant for liquids). By understanding this relationship, firefighters can adjust the nozzle to control how much water flows, ensuring effective suppression of the flames.
Momentum Change and Force Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Same way if you can just interpret it that the divergence of rho v v okay is nothing but momentum outflux per unit contour volume.
Detailed Explanation
This segment discusses how the divergence of the product of density and velocity yields insights into the momentum change within a control volume. Essentially, the divergence captures the balance of momentum entering and leaving the volume. This is relevant in applications like predicting how a fluid behaves when it accelerates or where forces act within it.
Examples & Analogies
Imagine a car racing down a highway. The momentum of the car changes based on how fast it accelerates or decelerates. Similarly, in fluid flow, the momentum of the fluid changes as it moves through different areas of pressure and velocity, impacting how far and fast it travels.
Newton's Second Law and Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at that what we are deriving this that we are not bringing a new physics to that.
Detailed Explanation
This piece outlines how the equations derived are rooted in Newton's Second Law of Motion, which states that force equals mass times acceleration. When applied to fluids, this law helps derive the Navier-Stokes equations, showing that fluids behave predictably under certain forces. It emphasizes that understanding fluid dynamics hinges on principles established in classical physics.
Examples & Analogies
Consider pushing a full supermarket cart (mass) to get it moving (acceleration). The harder you push (force), the faster it accelerates. Fluid dynamics works under a similar principle—knowing the forces acting on fluids helps predict their movements, just like knowing how much force to apply moves the cart efficiently through the aisles.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Notation: Essential for representing physical quantities such as velocity and force in fluid dynamics.
-
Navier-Stokes Equations: Fundamental equations governing the motion of fluid substances.
-
Dimensional Analysis: A method used to verify the consistency of equations through dimensional checks.
-
Newtonian Fluids: Fluids with a constant viscosity that behave linearly under applied stress.
-
Non-Newtonian Fluids: Fluids that have a viscosity dependent on the rate of shear, often resulting in complex flow behaviors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of vector notation: The velocity vector can be represented as v = (vx, vy, vz) for fluid motion in three dimensions.
-
Example of dimensional analysis: Evaluating whether the units of a defined pressure gradient in fluid mechanics equate correctly to force per unit volume.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flows, vectors lead the way, they guide the path, come what may.
📖 Fascinating Stories
-
Imagine a factory where syrup flows through pipes. The viscosity affects how fast it moves; this is like Newtonian and non-Newtonian fluids in our world.
🧠 Other Memory Gems
-
Remember 'V-N-D', where V for Vectors, N for Newtonian, and D for Divergence.
🎯 Super Acronyms
The acronym 'M-D-F' can help remember Mass, Dimensional Analysis, and Force relating to fluid mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector
Definition:
A quantity that has both magnitude and direction, essential in physics for representing forces, velocity, and acceleration.
-
Term: Divergence
Definition:
A vector operation that quantifies the extent to which a vector field spreads out from a point.
-
Term: Gradient
Definition:
A vector operation that indicates the direction and rate of change of a scalar field.
-
Term: Newtonian Fluid
Definition:
A fluid with a constant viscosity that does not change under varying shear rates.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity changes with the shear rate applied.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations that describe the motion of fluid substances.
-
Term: Dimensional Analysis
Definition:
The process of checking the consistency of equations by evaluating the dimensions of physical quantities.
-
Term: Continuity Equation
Definition:
A principle that states mass cannot be created or destroyed in a closed system, leading to the equation of mass conservation.