Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
Unlock Audio Lesson
Good morning, everyone! Today, we are diving into the Navier-Stokes equations. Who can tell me why these equations are significant in fluid mechanics?
Are they the foundation for computational fluid dynamics?
Exactly! They form the basis for solving many complex fluid flow problems. The equations are derived from fundamental principles governing fluid motion. Remember, we need to pay attention to their assumptions!
What assumptions do we usually take with these equations?
Great question! Typically, we assume the fluid is incompressible and isothermal.
What do those terms mean?
Incompressible means the fluid’s density doesn't change, and isothermal means the temperature remains constant. We'll clarify these as we go along. Let’s summarize: the Navier-Stokes equations are crucial for analyzing fluid behavior within various conditions.
Key Terms: Newtonian vs. Non-Newtonian Fluids
Unlock Audio Lesson
Now, let’s discuss Newtonian and non-Newtonian fluids. Who can provide a brief definition of a Newtonian fluid?
Isn't it a fluid where the viscosity remains constant regardless of the shear rate?
That's correct! Non-Newtonian fluids, on the other hand, exhibit varying viscosities with changes in shear rates. Can anyone give examples of each?
Water is a Newtonian fluid, while ketchup is an example of a non-Newtonian fluid.
Excellent! It's important to recognize these distinctions, as they will affect how we use the Navier-Stokes equations. In a nutshell, Newtonian fluids show consistent behavior under stress, while non-Newtonian fluids vary—a crucial aspect in analyzing fluid flows.
Derivation of Navier-Stokes Equations
Unlock Audio Lesson
Let’s move to the derivation of the Navier-Stokes equations from the Cauchy momentum equations. What do we start with?
We start from the linear momentum equation or Cauchy equations.
Correct! When applying the control volume approach, we break down forces like body forces and surface forces. Can anyone explain what we mean by body force?
It's the force acting throughout the volume of fluid, like gravity.
Exactly, while surface forces act at the boundary, exerting pressure on the fluid. Remember: the equation is driven by these forces acting on a fluid element over time. This leads us to our derivations in cylindrical coordinates, simplifying many problems.
Understanding Cylindrical Coordinates
Unlock Audio Lesson
Cylindrical coordinates often simplify problems involving rotation or flow in pipes. Who remembers the coordinates involved?
There are r, θ, and z coordinates.
Exactly! Let's explore the importance of these coordinates in describing fluid flow, especially in engineering applications. What challenges do we face when using these coordinates?
They look more complicated than Cartesian coordinates.
That’s true, but they provide a better framework for certain fluid motions. Understanding how to apply and manipulate these coordinates is key.
Application of Boundary Conditions
Unlock Audio Lesson
Now that we have introduced the equations, let’s discuss boundary conditions. What do we mean by that?
They are the constraints that define how the fluid behaves at the edges of the domain.
Exactly! Getting these right ensures we get realistic solutions to fluid behavior. Which boundary conditions could we consider for a fluid flowing through a pipe?
We could use no-slip conditions at the wall.
Yes! No-slip means the velocity at the boundary is zero. Remember, applying the correct boundary conditions is crucial for accurately solving Navier-Stokes equations effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Navier-Stokes equations are foundational in computational fluid dynamics and complex fluid flow problems. This section details their derivation in cylindrical coordinates, along with a review of relevant definitions such as Newtonian and non-Newtonian fluids. The assumptions of incompressible, isothermal flow are emphasized, paving the way for solving fluid mechanics problems with appropriate boundary conditions.
Detailed
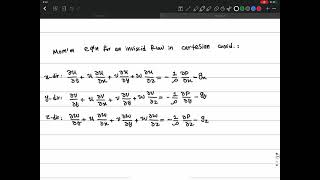
Navier-Stokes in Cylindrical Coordinates
The Navier-Stokes equations represent a set of nonlinear partial differential equations fundamental to fluid mechanics. In this section, we delve into their derivation within the framework of cylindrical coordinates. These equations serve as the cornerstone of computational fluid dynamics and are applicable to various complex fluid flow scenarios.
Key Points Covered:
- Historical Context: The equations owe their foundation to independent derivations by Claude-Louis Navier and George Stokes around 200 years ago.
- Definitions and Assumptions: We review concepts of Newtonian fluids, in which shear stress is linearly correlated with shear rate, as opposed to non-Newtonian fluids. We further discuss two critical assumptions — incompressibility (density remains constant) and isothermal flow (temperature remains constant throughout the flow).
- Mathematical Derivations: The section emphasizes the derivation of the equations under the assumptions of incompressible flow, using the Cauchy momentum equations as a starting point. The control volume approach provides us insight into local and convective accelerations, showcasing how body force and surface force influence fluid dynamics.
- Fluid Behavior in Cylindrical Coordinates: We explore how the equations translate into cylindrical coordinates, which is essential for certain applications in fluid mechanics.
- Boundary Conditions: The importance of appropriate boundary conditions for solving the Navier-Stokes equations is outlined, guiding students toward practical application in real-world scenarios.
Youtube Videos
![Navier-Stokes in cylindrical coordinates [Fluid Mechanics #9a]](https://img.youtube.com/vi/mkb9y8N2y_Q/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go to the next slides as you look it from Cauchy equations what we get it just in vector forms. In vector form if you remember it which is the linear momentum equations deriving with the components like rho by rho t rho v is velocity plus is equal to del dot product of rho v is equal to rho g is a vectors plus we have the del product or divergence of the stress tensor.
Detailed Explanation
The Navier-Stokes equations describe the motion of fluid substances. This particular introduction discusses how to express these equations in vector form. The equation essentially balances forces acting on a fluid element, such as pressure forces, viscous forces, and body forces like gravity. In mathematical terms, the equation includes terms for the fluid's density (rho), velocity (v), gravitational forces (g), and the divergence of the stress tensor. This sets the groundwork for analyzing fluid flow mathematically.
Examples & Analogies
Imagine trying to push a rubber duck through water. The forces acting on it include the force of the water pushing back against it (pressure), the force due to the duck's weight (gravity), and the internal friction of the water (viscosity) that affects how quickly it moves. Understanding these forces helps us predict the duck's movement, similar to how the Navier-Stokes equations help predict fluid motion.
Definitions of Divergence and Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the the vectors divergence okay. If you look at that del and V the velocity divergence it is talking about the net volume outflow from a control volume. So if you derive a simple equations as find out the velocity divergence what it says that what you will understand from that if you physical interpretations of that is a volume outflow per unit volume per unit control volume.
Detailed Explanation
The concept of divergence in fluid mechanics is crucial for understanding how fluid moves in and out of a control volume (a specified region in space). The divergence of velocity (denoted as 'del dot V') indicates how much fluid is leaving or entering that region over time. A positive divergence means more fluid is leaving than entering, possibly indicating a leak, while a negative divergence suggests fluid is accumulating in the volume.
Examples & Analogies
Think of a balloon being inflated. The air going into the balloon represents a negative divergence (fluid entering the control volume), while a hole in the balloon would create a positive divergence (fluid escaping the control volume). Understanding divergence helps in situations like predicting how quickly a buoyant object will rise in water.
Components of Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These two can indicating for us two force component one is body force another is the surface force that is what body force and the surface force component.
Detailed Explanation
In fluid mechanics, forces acting on a fluid can be categorized into two types: body forces and surface forces. Body forces, like gravity, act throughout the volume of the fluid. Surface forces, such as pressure and viscous forces, act on the boundaries of the fluid. Recognizing these distinctions allows for a clearer understanding of how different forces impact fluid movement and behavior.
Examples & Analogies
Imagine a leaf floating on a pond. The weight of the leaf pulling it downwards is a body force (gravity), while the water pushing up against the leaf's surface is a surface force (buoyancy). Considering both types of forces helps us understand why the leaf floats or sinks.
Cauchy's Equations and Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the basic equations is this part whether you can have this. Just to demonstrate it that we are discussing the velocity field, we are discussing about density field, we are discussing about the pressure field.
Detailed Explanation
Cauchy’s equations describe the motion of fluids in terms of velocity, density, and pressure fields. These fields help visualize how fluid moves and changes within a control volume. By analyzing these equations, we can describe how quantities like velocity and pressure vary in space and time, leading to a better understanding of fluid dynamics.
Examples & Analogies
Consider pouring syrup into a jar. The syrup's movement represents the velocity field, while the syrup's thickness indicates the pressure field. Observing how the syrup interacts with the jar (density) helps us predict how quickly it will pour out. Understanding these fields is crucial in various applications, from designing kitchen gadgets to predicting weather patterns.
Assumptions for Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
First is incompressible flow okay. That means density more or less fairly okay does not change with space as well as time.
Detailed Explanation
A core assumption when using the Navier-Stokes equations is that the fluid is incompressible, meaning its density remains approximately constant regardless of changes in pressure or temperature. This simplifies the equations, making them easier to solve, since we do not need to account for density variations that could complicate the fluid behavior.
Examples & Analogies
Think about drinking a thick milkshake through a straw. As you sip, the density of the milkshake doesn’t substantially change, despite the pressure you create by sucking on the straw. This approximation holds true for many common fluids, like water, which allows for simplified calculations in fluid dynamics.
Relationship Between Viscosity and Shear Stress
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that the same way we can always put a relationship between sigma the stress and the strain again I am hypo strain rate okay that is the reasons basic difference between the fluid mechanics and the solid mechanics.
Detailed Explanation
In fluid mechanics, the relationship between shear stress and shear strain rate is foundational. This relationship, represented by Newton's law of viscosity, states that shear stress is proportional to the rate of deformation (strain rate). This contrasts with solid mechanics, where the relationship is between stress and strain. This distinction is essential for analyzing how fluids respond to applied forces.
Examples & Analogies
Imagine spreading butter on toast. The stress you apply (the pressure of the knife on the butter) translates into strain (the butter changing shape). In fluids, we often see this relationship in motion. For example, honey flows slowly out of a jar due to its viscosity, which describes how it resists flow under stress.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations representing fluid motion.
-
Newtonian Fluids: Viscous behavior that remains constant with shear.
-
Non-Newtonian Fluids: Viscosity that changes with shear rate.
-
Incompressible Flow: Flow characterized by constant density.
-
Isothermal Flow: Flow at constant temperature.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing in a pipe is an example of a Newtonian fluid, while toothpaste is a non-Newtonian fluid.
-
The behavior of fluid jets in industrial applications often requires the use of Navier-Stokes equations in cylindrical coordinates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flow, density's unchanging, temperature remains, in isothermal straining.
📖 Fascinating Stories
-
Once upon a time, in a cylindrical world, fluids whirled and twirled, following the Navier-Stokes code, where temperature and density decided their load.
🧠 Other Memory Gems
-
To remember the assumptions, think: I-N (Incompressible, isothermal) are key!
🎯 Super Acronyms
NICE for Navier-Stokes
- Newtonian
- Incompressible
- Constant temperature
- Equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
Equations that describe the motion of viscous fluid substances.
-
Term: Newtonian Fluid
Definition:
A fluid whose viscosity remains constant regardless of shear rate.
-
Term: NonNewtonian Fluid
Definition:
A fluid whose viscosity varies with a change in shear rate.
-
Term: Incompressible Flow
Definition:
A flow in which the density of the fluid remains constant.
-
Term: Isothermal Flow
Definition:
A flow where the temperature is constant throughout the fluid.
-
Term: Cauchy Momentum Equation
Definition:
The fundamental law that governs the motion of fluid particles.
-
Term: Control Volume
Definition:
A defined physical volume through which fluid can flow, used in the analysis of fluid systems.