Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Stress Tensor
Unlock Audio Lesson
Good morning, class! Today, we'll delve into the properties of the stress tensor. Can anyone explain what the stress tensor is in the context of fluid mechanics?
Is it related to how fluids exert forces on each other?
Exactly! The stress tensor describes how internal friction and pressure within a fluid influence its motion. It's a critical aspect of the Navier-Stokes equations. Can anyone tell me the significance of the Navier-Stokes equations?
They're used to model fluid flow, right?
Correct! They describe the conservation of momentum in fluid flow. The stress tensor is an essential part of these equations as it encapsulates the forces acting within the fluid.
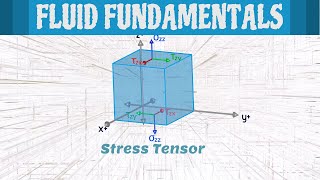
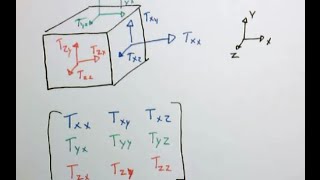
Components of the Stress Tensor
Unlock Audio Lesson
Let's break down the stress tensor's components. Who can explain the terms σ_ij in the tensor?
Isn't σ_ij the stress acting on the fluid particle faces?
That’s right! Each component of the tensor represents the stress acting in a specific direction. Remember that the tensor is a 3x3 matrix for three-dimensional flow. Any thoughts on the physical meaning of these stress components?
They represent the internal forces? Like shear and normal stresses?
Yes! The diagonals represent normal stresses, while the off-diagonal elements represent shear stresses. Understanding these components helps us predict how fluids behave under various conditions.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Lesson
Now, let's discuss fluid types. What differentiates Newtonian fluids from non-Newtonian ones concerning the stress tensor?
Newtonian fluids have a constant viscosity, right? So the stress is directly proportional to the strain rate.
Exactly! In Newtonian fluids, the relationship between shear stress and strain rate is linear. What about non-Newtonian fluids?
They don't have a constant viscosity; their stress response varies with strain rate.
Correct. Therefore, modeling their behaviors requires more complex relationships. The implications of this for engineering applications are significant, especially in biomedical fields!
The Navier-Stokes Equations
Unlock Audio Lesson
Let's look at the Navier-Stokes equations in detail. Who remembers the assumptions we make when deriving these equations?
We assume incompressible and isothermal flows, right?
Exactly! These assumptions simplify the equations significantly. Incompressibility means density remains constant, while isothermal flow indicates that temperature doesn't change significantly. Why are these assumptions crucial?
They help reduce the complexity of the equations, making them easier to solve.
Precisely! The Navier-Stokes equations form the foundation of computational fluid dynamics. In our next classes, we’ll explore specific applications and solve some example problems using these principles.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The properties of the stress tensor are critical in understanding fluid motion. This section explores the derivation of the Navier-Stokes equations, the distinctions between Newtonian and non-Newtonian fluids, and the importance of stress tensor components in analyzing fluid behavior.
Detailed
In fluid mechanics, the stress tensor plays a vital role in the study of fluid behavior and dynamics. This section introduces the stress tensor as a fundamental construct used in the Navier-Stokes equations, which govern fluid motion. The section explains the significance of Cauchy's equations, the definition and interpretation of the stress tensor, its components, and its relation to momentum equations within control volumes. Key distinctions between Newtonian and non-Newtonian fluids are discussed, highlighting the implications for viscosity and flow behavior. The exploration of the Navier-Stokes equations, including the assumptions made for incompressible and isothermal flows, deepens the understanding of the mathematical framework used to analyze fluid motion. The section concludes with a discussion around challenges in solving these equations and the fundamental link between stress tensor properties and real-world fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Stress Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In vector form, if you remember it, which is the linear momentum equations deriving with the components like rho by rho t rho v is velocity plus is equal to del dot product of rho v is equal to rho g is a vectors plus we have the del product or divergence of the stress tensor. This is what we have derived as a Cauchy equations which is a linear momentum equations for infinitely small control volumes.
Detailed Explanation
The stress tensor is a mathematical representation that describes internal forces in a material. In fluid mechanics, it captures how forces are distributed within a fluid. The Cauchy equations express the linear momentum of a fluid, showcasing how the behavior of the fluid can be modeled using the stress tensor. Here, 'rho' represents density, and 'v' represents velocity; the equations essentially relate changes in momentum to stresses and forces acting on the fluid.
Examples & Analogies
Imagine a balloon filled with water. When you squeeze it, the water pushes against the walls of the balloon with pressure. This pressure can be calculated using the concepts in the stress tensor, which tells us how force (your hand's pressure) is distributed throughout the water (the fluid).
Physical Interpretation of Velocity Divergence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the vectors divergence okay. If you look at that del and V the velocity divergence it is talking about the net volume outflow from a control volume. It indicates the physical interpretations of velocity divergence.
Detailed Explanation
Velocity divergence helps us understand how much fluid is flowing out of a specified volume over time. Mathematically, if the divergence of velocity is positive, it indicates a net outflow of fluid from that region. Conversely, a negative divergence suggests that more fluid is entering the volume than leaving. This concept is critical in analyzing fluid flow because it directly relates to the conservation of mass.
Examples & Analogies
Consider a water faucet. When the tap is opened, water flows out, creating a divergence from the point of the faucet. If you imagine the water as a control volume, a positive divergence indicates more water is leaving the volume (the sink) than is entering, demonstrating how fluid conservation works in a simple system.
Components of Mass and Momentum Outflow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same way if I just put it the del into rho into v what is indicating is the mass outflow for a unit control volume.
Detailed Explanation
This equation describes how mass exits a control volume over time, linking density and velocity. The term 'del' indicates how mass changes across a small volume. Essentially, it tells us not just about the mass leaving but also how fast it's leaving, which is vital in understanding fluid dynamics, especially in systems where density can change (like air or water in different temperatures).
Examples & Analogies
Think about a sponge being squeezed. When you apply pressure (like the del operator), the mass of water that flows out of the sponge (the control volume) is directly related to how densely packed the water is in the sponge (density) and how hard you squeeze it (velocity). This demonstration can help visualize mass flow in a more tangible manner.
Understanding Force Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These two can indicating for us two force component one is body force another is the surface force that is what body force and the surface force component.
Detailed Explanation
In fluid dynamics, forces acting on a fluid element can be categorized as body forces or surface forces. Body forces, such as gravity, act throughout the volume of the fluid, while surface forces, like pressure or viscous forces, act on the boundaries of the fluid. Understanding these distinctions helps predict fluid behavior under various conditions, a fundamental aspect of fluid mechanics.
Examples & Analogies
Imagine a swimming pool. The water is subjected to gravity pulling it down (body force). At the pool’s surface, the water experiences tension and pressure from the air above it (surface forces). Recognizing these different forces helps understand why water moves and behaves the way it does in various situations.
Equations from Newton's Second Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that even if you do a vector notation we are deriving very basic Newton's second law is that force is equal to mass into accelerations.
Detailed Explanation
This concept reaffirms that fluid dynamics, much like solid mechanics, adheres to Newton's second law of motion, where forces result in acceleration. When applied to fluids, this means that forces acting on a control volume lead to changes in movement. While fluid dynamics introduces complexities like viscosity and compressibility, the foundational principles remain consistent with Newton's laws.
Examples & Analogies
Think of a soccer ball sitting still and then being kicked. The force from the kick causes the ball (mass) to accelerate in the direction of the kick due to Newton's second law. In fluid mechanics, if you consider a section of water, applying a force will cause it to move or change speed, similarly to the soccer ball.
Stress Tensor Components and Their Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Navier-Stokes equations do that approximations. to reduce this unknowns the 10 unknowns to the 4 unknowns.
Detailed Explanation
The Navier-Stokes equations represent a set of partial differential equations that describe how the velocity field of a fluid evolves over time based on various forces and stresses. With several variables involved, the equations can seem complex. By making specific assumptions (like incompressibility), we can reduce the number of unknowns, simplifying the problem to a manageable form.
Examples & Analogies
Imagine organizing a large stack of books. You start with many books (unknowns), but to make it easier, you decide to only focus on a few key sections you need right away (reducing the unknowns). In fluid dynamics, simplifying the Navier-Stokes equations helps you handle complex flow scenarios in a similar way, allowing easier focus on essential aspects of flow behavior.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress Tensor: Represents internal forces and is crucial in fluid dynamics.
-
Newtonian Fluids: Characterized by a linear relationship between shear stress and strain rate.
-
Non-Newtonian Fluids: Exhibit variable viscosity and do not obey simple linear relationships.
-
Navier-Stokes Equations: Govern fluid motion and require specific assumptions to simplify their solutions.
-
Incompressible and Isothermal Flows: Fundamental assumptions that ease the complexity of fluid flow analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The behavior of water (a Newtonian fluid) flowing through a pipe, illustrating constant viscosity.
-
The flow of ketchup (a non-Newtonian fluid) which thickens and flows differently depending on the applied force.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress tensor’s core, forces galore; Newtonian’s a line, non-Newt's outshine!
📖 Fascinating Stories
-
Imagine a river (Newtonian) flowing steadily, water moves smoothly without much change. Now picture ketchup (non-Newtonian), getting pushed and pulled, changing how it flows - that's the two types of fluids!
🧠 Other Memory Gems
-
For Newtonian, remember 'N' for constant viscosity; for Non-Newtonian, 'V' for variable viscosity.
🎯 Super Acronyms
NVS - Newtonian, Variable viscosity, Shear stress proportional.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical representation of the internal distribution of forces within a fluid.
-
Term: Newtonian Fluid
Definition:
Fluids with a constant viscosity, where shear stress is linearly proportional to the shear strain rate.
-
Term: NonNewtonian Fluid
Definition:
Fluids where the viscosity changes with the shear rate, leading to a non-linear relationship between shear stress and strain rate.
-
Term: NavierStokes Equations
Definition:
Fundamental equations in fluid dynamics that describe the motion of fluid substances.
-
Term: Incompressible Flow
Definition:
A flow in which the fluid density remains constant.
-
Term: Isothermal Flow
Definition:
A flow condition where the temperature remains constant throughout the fluid.
-
Term: Cauchy's Equations
Definition:
Equations of motion that relate the stress tensor to the rate of momentum change in a fluid.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to deformation or flow.