Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Historical Context of Navier-Stokes Equations
Unlock Audio Lesson
Good morning, everyone! Today, let's start by understanding who Navier and Stokes are and why their equations are so vital to fluid mechanics. Does anyone know when these equations were developed?
Was it around 200 years ago?
Exactly! Claude-Louis Navier and George Stokes published their findings independently about two centuries ago. Their work laid the groundwork for the Navier-Stokes equations. Can someone tell me what these equations help us solve?
They help in understanding fluid flow problems?
Right! They are foundational in computational fluid dynamics. Remember this: ‘Navier-Stokes = Fluid Flow.’ Let's delve deeper into their applications.
Understanding Cauchy's Equations
Unlock Audio Lesson
Now, let's discuss **Cauchy's equations**. Can anyone explain what they represent in fluid dynamics?
They are the linear momentum equations that involve stress tensors?
Correct! They give us crucial relationships. When we consider a small control volume of fluid, these equations become pivotal. Who can represent them in vector form?
Uh, is it something like rho dv/dt = rho g + del·σ?
Absolutely! Great job! This equation works through the relationships of forces acting on the fluid, which we will simplify later.
Assumptions in Momentum Equations
Unlock Audio Lesson
Let’s explore the assumptions behind the Navier-Stokes equations. What do we mean by incompressible and isothermal flow?
Incompressible flow means the density remains constant, right?
Exactly! And isothermal flow indicates that the temperature remains unchanged within the fluid. Why do you think these assumptions are important?
I guess it simplifies the equations to workable forms?
Correct! These assumptions make the mathematical handling of the equations feasible. At this point, who can describe how these lead to the derivation of the stress tensor?
Deriving the Navier-Stokes Equations
Unlock Audio Lesson
Now it’s time to derive the **Navier-Stokes equations**! Can anyone start by writing the equation forms, factoring in our previous discussions?
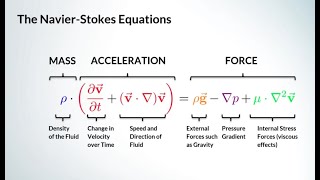
So, we have: ρ(dv/dt) = −∇P + μ∇²v + ρg?
Exactly! This shows the pressure gradient, viscous forces, and body forces like gravity acting within the fluid. What does the term μ represent here?
It’s the dynamic viscosity of the fluid!
Well done! This framework allows us to analyze the dynamics of incompressible fluid flows appropriately. Remember—'Viscosity = Resistance!'
Coordinate Systems in Fluid Dynamics
Unlock Audio Lesson
Lastly, let's discuss coordinate systems. Why is it important to use different coordinate systems in fluid mechanics?
Different systems can make the equations easier to solve depending on the geometry of the problem?
Correct! We often switch between Cartesian and cylindrical coordinates. Can someone give an example of when you'd use cylindrical coordinates?
In situations involving pipes or cylindrical shapes?
Exactly! Always remember to align your coordinate systems with the flow characteristics. This makes problem-solving much more intuitive.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the derivation of Navier-Stokes equations, which are fundamental to computational fluid dynamics. It discusses the history of their formulation, the assumptions made in incompressible, isothermal flows, and the significance of Cauchy's equations in establishing relationships between stress, velocity, and acceleration.
Detailed
Detailed Summary
The section on Deriving Momentum Equations provides a comprehensive overview of the momentum conservation principles in fluid mechanics, particularly through the lens of the Navier-Stokes equations. These equations are essential for understanding complex fluid flow problems and form the foundation of computational fluid dynamics (CFD).
Historical Context
Claude-Louis Navier and George Stokes independently formulated the equations that bear their names around 200 years ago. Their combination of physics and mathematics made significant contributions to fluid mechanics.
Key Features of Navier-Stokes Equations
The section emphasizes key concepts such as:
- Cauchy's equations: These present the linear momentum equations and help clarify the role of stress tensors in fluid dynamics.
- Incompressible vs. Non-Newtonian Fluids: The derivation begins with the examination of Newtonian fluids, where stress and strain rates maintain a linear relationship.
- Assumptions for Simplification: The focus is on incompressible and isothermal flow, leading to simpler forms of the equations.
Mathematical Formulation and Components
The complex vector notations are simplified into a manageable form through derivation, highlighting the interplay between:
- Body forces (e.g., gravity)
- Surface forces (e.g., viscous effects)
The derived Navier-Stokes equations reflect how velocity changes under various forces acting upon a fluid mass, leading to a clearer understanding of the dynamics at play. Despite their foundational role, these equations present significant challenges, notably when seeking analytical solutions due to their non-linear and time-dependent nature.
The exploration of coordinate systems, both Cartesian and cylindrical, further illustrates the versatility and application of these equations in real-world fluid dynamics scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning all of you. Today we are going to discuss about very interesting topics, the topics on Navier-Stokes equations. That is what the basic foundations of computational fluid dynamics and many of the complex fluid flow problems also we can solve it by using Navier-Stokes equations.
Detailed Explanation
In this introduction, the speaker sets the stage for discussing the Navier-Stokes equations, which are essential in the field of fluid mechanics. These equations form the basis of computational fluid dynamics (CFD) and help in solving complex problems related to fluid flow. The Navier-Stokes equations are fundamental to understanding how fluids behave under various conditions, making them crucial for engineers and scientists.
Examples & Analogies
Think of the Navier-Stokes equations as the rules of a game played by fluid particles. Just as players follow rules to move a ball—like passing or shooting—fluids follow mathematical equations to move and interact with their environment. Understanding these equations allows us to predict fluid behavior, just as knowing game rules allows players to anticipate actions in a game.
Historical Background
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
if you look go through its who is Navier and who is Stokes okay the way back the French physicist okay Claude-Louis Navier okay so it is almost 200 years back and also this George Stokes from as a mathematicians from England both have derived the Navier-Stokes equations independently.
Detailed Explanation
The Navier-Stokes equations are named after two individuals, Claude-Louis Navier and George Stokes, who developed them over 200 years ago. Navier was a physicist from France, while Stokes was a mathematician from England. They independently derived these equations, contributing to the mathematical treatment of fluid dynamics. Their work has been validated and built upon, leading to the comprehensive theories we use today.
Examples & Analogies
Imagine inventors who create a groundbreaking device, like a smartphone. One inventor might work on the software while another develops the hardware, and both are unaware of each other's discoveries. Their combined work ultimately leads to the final product that revolutionizes communication. Similarly, Navier and Stokes independently tackled fluid equations, and their separate contributions merged to form the foundation of fluid dynamics.
Newtonian vs Non-Newtonian Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I will talk about start from a introductions part. Also, I will talk about revisit Newtonian fluid and non-Newtonian fluid part which is quite interesting to look at how we can use for this Navier-Stokes equations.
Detailed Explanation
In fluid mechanics, fluids are classified as Newtonian or non-Newtonian based on their behavior when they flow. Newtonian fluids, like water, have a constant viscosity, meaning they flow consistently regardless of the applied stress. Non-Newtonian fluids, like ketchup, can behave differently; their viscosity can change based on the force applied, often flowing more easily under certain conditions or becoming thicker when stirred. Understanding these differences is critical when applying the Navier-Stokes equations since they assume a certain fluid behavior.
Examples & Analogies
Consider syrup and water. When you pour water, it flows readily and consistently; this is like a Newtonian fluid. Now, think about syrup, which flows slowly and thickly at first but becomes more fluid-like when shaken—this shows its non-Newtonian behavior. Knowing how to handle different fluids in recipes is similar to how engineers must adjust their calculations for different fluid types when using the Navier-Stokes equations.
Cauchy's Equations and Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it from Cauchy equations what we get it just in vector forms. In vector form if you remember it which is the linear momentum equations deriving with the components like rho by rho t rho v is velocity plus is equal to del dot product of rho v is equal to rho g is a vectors plus we have the del product or divergence of the stress tensor.
Detailed Explanation
Cauchy's equations describe motion based on momentum conservation inside a fluid. Using vector notation, they represent the relationship between fluid density (rho), velocity (v), external forces such as gravity (g), and stress within the fluid. The equations consider changes over time (∂/∂t) and spatial variations, allowing us to derive the dynamic behavior of the fluid. This lays the groundwork for the momentum equations we derive later from the Navier-Stokes framework.
Examples & Analogies
Think of a crowded highway where cars (representing fluid elements) are moving. The speed of each car (velocity) changes based on how many cars are on the road (density) and how much pressure there is from behind (stress). Cauchy's equations help us analyze how these factors influence traffic flow, just as Navier-Stokes equations help in analyzing fluid behavior.
Understanding Divergence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the the vectors divergence okay. If you look at that del and V the velocity divergence it is talking about the net volume outflow from a control volume.
Detailed Explanation
In fluid dynamics, the term 'divergence' refers to a mathematical operation that measures how much a vector field spreads out from a point. Specifically, the divergence of velocity indicates how much fluid is exiting or entering a control volume. A positive divergence means fluid is flowing out, while a negative divergence means fluid is flowing in. Understanding this helps us quantify flow rates and mass conservation, which are critical for applying the Navier-Stokes equations.
Examples & Analogies
Imagine a fire hose spraying water. The area where water flows out has a positive divergence because water is leaving that space, while the area where water is sucked back in, such as from a drain, has negative divergence. By measuring how much water exits versus what enters, you can better manage water flow, much like how engineers manage fluid flows in their designs.
Newton's Second Law in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at this Chezy's equations if you have simple derivations alternative form okay which more derivations you can just go through the derivations go through the Senzel and Cimbala book. I am not deriving one by one.
Detailed Explanation
Chezy's equations are a form of the momentum equations applied to fluid flow. They stem from Newton's second law (force equals mass times acceleration) applied to a control volume within the fluid. This means calculating the forces acting on a small volume of fluid and relating it to changes in motion. This foundational understanding is necessary to derive the Navier-Stokes equations accurately.
Examples & Analogies
Consider a skateboarder on a flat surface. The push of their legs (force) leads to acceleration, propelling them forward. In fluid dynamics, Chezy's equations analyze similar forces and movements in fluid flow, providing a mathematical way to understand how feeble pushes can lead to massive motions, like a river's flow.
Moment Changes and Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I try to interpret this physically this part nothing else that is what change in momentum okay. Here we have a linear momentum within the control volume with respect to time.
Detailed Explanation
This chunk discusses the relationship between changes in momentum within a control volume in relation to time. It emphasizes understanding how momentum changes due to outside forces such as body forces (gravity, for example) and surface forces (shear stress from fluid viscosity). This sets the stage for expressing the Navier-Stokes equations and how they account for these various forces acting on fluids.
Examples & Analogies
Think about how a swimmer pushes the water behind them to propel themselves forward. The force they exert changes the water's momentum, influenced by both their movements (surface force) and the water pushing against gravity (body force). The Navier-Stokes equations help model these interactions mathematically, allowing predictions of swimming techniques' effectiveness depending on the swimmer's style and technique.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Navier-Stokes Equations: Essential equations governing fluid motion.
-
Cauchy's Equations: Fundamental relationships describing stress in fluid dynamics.
-
Incompressible Flow: Flow condition where density remains unchanged.
-
Viscosity: The property of a fluid that quantifies its resistance to flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a river's flow can be understood using the Navier-Stokes equations to analyze velocity, pressure, and shear stress.
-
Blood flow in human veins can be modeled using the principles derived from the Navier-Stokes equations, considering viscosity and various gradients.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Navier and Stokes, fluid provokes, equations for flow, where pressure invokes.
📖 Fascinating Stories
-
Once upon a time, fluids roamed fierce rivers. Navier and Stokes bridged their flow, crafting equations to understand their swift behavior.
🧠 Other Memory Gems
-
V-P-B: 'Viscosity = Pressure - Body forces'. A way to remember what influences fluid movement!
🎯 Super Acronyms
ICE
- 'Incompressible
- Constant temperature
- Equal forces'. To remember the basic assumptions for Navier-Stokes.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of equations describing the motion of fluid substances, fundamental in fluid mechanics.
-
Term: Cauchy's Equations
Definition:
Linear momentum equations for fluid that relate stress and momentum within a control volume.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density remains constant over time.
-
Term: Isothermal Flow
Definition:
Flow where the temperature remains constant throughout the fluid.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow, impacting the fluid's behavior under stress.
-
Term: Stress Tensor
Definition:
A mathematical construct that describes stress in a fluid at a point, accounting for both normal and shear stress.
-
Term: Body Force
Definition:
A force that acts throughout the volume of a fluid, like gravity.
-
Term: Surface Force
Definition:
Force that acts on the surface of, or at the boundary of a fluid.