Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cauchy Equations and Fluid Dynamics
Unlock Audio Lesson
Welcome everyone! Today we will dive into the derivation of Cauchy equations, which is fundamental for understanding fluid dynamics. Can anyone tell me who Cauchy is and why these equations matter?
Cauchy was a mathematician who worked on fluid mechanics, right?
Exactly! Cauchy, along with Navier and Stokes, contributed to the understanding of fluid motion. Why do you think it’s important to consider both body forces and surface forces in fluid dynamics?
Well, because fluids are affected by both external forces, like gravity, and internal stresses!
Right again! Now, let's remember: Cauchy equations express the balance of linear momentum acting on a control volume, which helps us analyze fluid behavior in various scenarios.
Vector Notation and Stress Tensor
Unlock Audio Lesson
Next, we want to focus on vector notation and how it relates to Cauchy equations. Can anyone explain what the divergence of velocity represents?
I think it represents the volume outflow from a control volume, right?
Remember that stress tensors have different components like sigma_ij?
Yeah, and they can change based on the directions they're applied in!
Correct! It’s important to visualize how stresses act on different surfaces of a control volume.
Newton's Second Law and Fluid Dynamics
Unlock Audio Lesson
Now, let’s discuss how Newton's second law applies to fluids. Who can recall what the law states?
It's the principle that force equals mass times acceleration.
Exactly! So, in fluid dynamics, we apply this principle to control volumes. How can we think of forces acting on a fluid element?
With both surface and body forces! Like gravity and shear stresses.
Great job! The real challenge is deriving Cauchy's equations from this principle while considering all forces involved.
Assumptions in Deriving the Navier-Stokes Equations
Unlock Audio Lesson
Let's now analyze the main assumptions we make for deriving the Navier-Stokes equations. Who can mention one?
Assuming the flow is incompressible?
That's one! Incompressible flow allows us to simplify equations significantly. What about isothermal conditions?
Isothermal means the temperature remains constant in the flow, right?
Right! These assumptions reduce complexity in our calculations. Can anyone think of an example of where these assumptions might apply?
Like water flowing in a pipe?
Exactly! That's a perfect application. Understanding these underlying assumptions is crucial for solving real-world problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the derivation of Cauchy's equations, discussing their connection to the Navier-Stokes equations and the fundamental principles of fluid mechanics, emphasizing the concepts of linear momentum, control volume, and the role of stress tensors.
Detailed
Deriving Cauchy Equations
The Cauchy equations are a set of equations fundamental to fluid mechanics, detailing the motion of fluid elements through the principles of linear momentum and stress. The section opens with an introduction to the Navier-Stokes equations, which are derived from Cauchy's equations, fostering an understanding of complex fluid flow problems. The essential background information on the physicists involved in the derivation—Claude-Louis Navier and George Stokes—sets the stage for their significance.
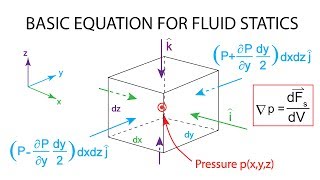
Cauchy's equations can be expressed in vector notation, where each term corresponds to various variables influencing fluid motion. These equations link fluid behavior to forces, including body forces from external influences such as gravity and surface forces related to stress tensors. Understanding the divergence operator is crucial as it provides insight into fluid outflow from control volumes.
The section further delves into Newton's second law, conveying the relationship between force, mass, and acceleration within fluid systems. The stress tensor’s components are explored, illustrating how they transform in different coordinate systems, establishing the connection between fluid dynamics and vector theory.
In the latter part, the section discusses assumptions made for deriving the Navier-Stokes equations, notably regarding incompressibility and isothermal flows. This establishes a solid foundation for transitioning into more complex fluid flow equations and their applications in computational fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Cauchy Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
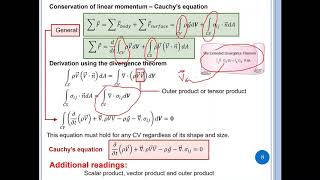
If you look at from Cauchy equations what we get it just in vector forms. In vector form if you remember it which is the linear momentum equations deriving with the components like rho by rho t rho v is velocity plus is equal to del dot product of rho v is equal to rho g is a vectors plus we have the del product or divergence of the stress tensor. This is what we have derived as a Cauchy equations which is a linear momentum equations for infinitely small control volumes.
Detailed Explanation
Cauchy equations emerge from fluid mechanics and describe the momentum balance in fluid systems. The equation can be broken down into components that relate changes in fluid velocity (rho by rho t rho v) to forces acting on the fluid. The term 'del dot product of rho v' represents the change in momentum due to fluid motion, while 'rho g' represents the gravitational force acting on the mass of the fluid. Finally, the divergence of the stress tensor encompasses the internal forces acting within the fluid, illustrating how pressure and viscous components interact.
Examples & Analogies
Imagine holding a heavy bucket of water. As you lift the bucket, the water inside moves and wants to push against the sides of the bucket due to its weight (analogous to the weight force rho g). If you suddenly stop lifting, the water also pushes back against the bottom of the bucket as it decelerates (related to changes in momentum). The complexities of these forces in motion and at rest are encapsulated in Cauchy’s equations.
Interpretation of Velocity Divergence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you go back very basic things, the the vectors divergence okay. If you look at that del and V the velocity divergence it is talking about the net volume outflow from a control volume okay.
Detailed Explanation
Velocity divergence quantifies the rate at which fluid is expanding or contracting in a given volume. It is calculated through 'del dot V', where 'V' is the velocity vector. When the divergence is positive, it indicates that more fluid is flowing out of the control volume than flowing in, leading to an expansion of fluid (net outflow). Conversely, a negative divergence suggests that fluid is being 'sucked' into the volume, resulting in a contraction.
Examples & Analogies
Think of a deflating balloon. As the air leaves the balloon, the volume decreases, leading to negative divergence as the air leaves. Conversely, if you were to blow up the balloon, it would expand and have a positive divergence, since more air is entering than leaving.
Interpreting Mass Outflux and Momentum Changes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The same way if I just put it the del into rho into v what is this is indicating is the mass outflow for a unit control volume.
Detailed Explanation
When you multiply the density (rho) by the velocity (V) and apply the divergence operator, you effectively assess mass flow in and out of a control volume. This concept captures how changes in fluid density and velocity contribute to the mass balance within the control volume.
Examples & Analogies
Consider water flowing through a pipe. If you know the speed of the water (velocity) and how dense it is (mass), you can determine how much water is flowing out of or into sections of the pipe. If you observe a section of the pipe that is widening, you might find that as water moves through at the same speed, the amount flowing out might change based on the new area it passes through.
Understanding Forces in Fluid Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These two can indicating for us two force component one is body force another is the surface force that is what body force and the surface force component.
Detailed Explanation
Fluid dynamics entails both body forces (like gravity acting on a fluid mass) and surface forces (resulting from pressure and shear stress at the boundaries of a control volume). Each of these force types impacts fluid flow. Body forces act through the volume of the fluid, whereas surface forces act on the fluid's surface resulting in changes in velocity and direction.
Examples & Analogies
Consider a boat on a lake. Gravity is the body force pulling it down, while the push of water against the base of the boat is the surface force that helps keep it afloat. As the wind blows (an external force), it can alter the boat's movement by affecting its surface in combination with the body forces.
Connecting Cauchy’s Equations to Newton’s Laws
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that what we are deriving this that we are not bringing a new physics to that. The same concept we are talking about that we know from Newton s second laws the force is equal to mass into acceleration.
Detailed Explanation
Cauchy’s equations are fundamentally linked to Newton’s second law of motion, which posits that the net force acting on an object (or control volume) equals its mass multiplied by its acceleration. This classical law translates into fluid dynamics as you consider how forces (both internal and external) affect fluid behavior and momentum changes.
Examples & Analogies
Think about a car accelerating from a stop. The acceleration depends on how much fuel (mass) you have in the tank and how much force the engine generates. Similarly, in fluid dynamics, just like the car can speed up or slow down due to these forces, fluids behave based on their net forces.
Previewing the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let me go for the next part which is Navier-Stokes equations okay. What the Navier-Stokes equations are did it and what is the problems was there from Cauchy's equations if the problems or the mathematical challenges.
Detailed Explanation
The Navier-Stokes equations extend the principles described by Cauchy equations, incorporating the effects of viscosity into flow dynamics. They aim to provide a more comprehensive mathematical model for fluid motion under varying conditions. Specifically, they address limitations of Cauchy equations by offering a framework that accounts for complex fluid behavior, allowing scientists and engineers to solve real-world problems in fluid mechanics.
Examples & Analogies
Imagine trying to calculate how honey flows compared to water. While both fluids follow similar gravitational principles, honey’s thickness (viscosity) needs to be accounted for in calculations. The Navier-Stokes equations help provide those calculations that Cauchy's equations, which assume simpler behavior, can't cover.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Cauchy Equations: Describe fluid motion in terms of forces and stresses.
-
Control Volume: A defined region for analyzing fluid flow phenomena.
-
Divergence: Measures how a fluid expands or contracts in a small volume.
-
Incompressibility: Assumes fluid density remains constant during flow.
-
Newton's Second Law: Fundamental principle linking force, mass, and acceleration.
-
Stress Tensors: Represent the internal flow stresses acting within a fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Analyzing the motion of water flowing through a pipe can be approached using Cauchy's equations to understand internal stresses.
-
Example 2: In aerodynamics, applying Cauchy's equations helps predict airflow behavior over an aircraft wing.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Cauchy's equations in fluid play, stress and forces lead the way.
📖 Fascinating Stories
-
Imagine a small pipe where water flows. The forces inside shape how it goes! Special equations guide its dance, leading to fluid's big advance.
🧠 Other Memory Gems
-
To remember the flow types, think: 'I N' for Incompressible and Isothermal!
🎯 Super Acronyms
Remember 'C.F.D.' for Cauchy Equations, Forces, and Dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Cauchy Equations
Definition:
Equations that describe the motion of fluid under the influences of stress and forces.
-
Term: NavierStokes Equations
Definition:
Set of equations that describe the motion of viscous fluid substances.
-
Term: Stress Tensor
Definition:
Mathematical representation of the internal forces within a fluid.
-
Term: Control Volume
Definition:
A defined space through which fluid flows, used for analysis.
-
Term: Divergence
Definition:
A mathematical operator that measures the rate of outflow of a vector field from an infinitesimal volume.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density remains constant.
-
Term: Isothermal Flow
Definition:
Flow in which the temperature is constant throughout the fluid.
-
Term: Body Force
Definition:
Force that acts throughout the volume of a fluid, such as gravitational force.
-
Term: Surface Force
Definition:
Force that acts on the surface of a fluid element, including pressure and viscous forces.