Introduction to Navier-Stokes Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are discussing the Navier-Stokes equations. Can anyone explain why these equations are significant in the study of fluids?

They help us understand how fluids move and behave in different conditions.

Exactly! They form the foundation of computational fluid dynamics. The equations help us model complex fluid flow problems. Who can tell me about their origin?

They were derived independently by Navier and Stokes over 200 years ago.

Correct! This collaboration between physics and mathematics was crucial for the development of fluid mechanics.
Physics Behind Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about the underlying principles. Who remembers the difference between Newtonian and non-Newtonian fluids?

Newtonian fluids maintain a constant viscosity regardless of the flow conditions, while non-Newtonian fluids can change their viscosity.

Right on! This distinction is essential when applying the Navier-Stokes equations. Now, why would this matter in real-world applications?

Because different fluids behave differently under stress, which affects engineering designs.

Absolutely! Understanding these properties allows us to design systems better, like in biomedical applications or aerospace engineering.
Derivation of the Navier-Stokes Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's dive into the derivation of the Navier-Stokes equations. Who remembers the Cauchy equations?

They describe momentum conservation in a fluid, right?

Exactly! By applying certain assumptions—like incompressibility and isothermal flow—we can simplify them to arrive at the Navier-Stokes equations. What does incompressible mean in this context?

It means the fluid’s density doesn't change significantly during flow.

Correct! And isothermal means the temperature remains constant. This simplification allows us to make some important generalizations about fluid movements. Remember these terms well!
Boundary Conditions and Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s shift our focus to boundary conditions. How do they impact our solutions?

They define how the fluid interacts with its environment, which can change the flow behavior.

Exactly! Boundary conditions are essential for applying Navier-Stokes equations effectively. Can anyone mention the coordinate systems we typically use?

Cartesian and cylindrical systems.

Spot on! Each system has its advantages depending on the flow scenario being analyzed.
Challenges and Computational Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s discuss the challenges faced in solving the Navier-Stokes equations. Why do you think it is difficult?

Because they are nonlinear and partial differential equations, which are hard to work with.

Correct! That's why computational fluid dynamics plays such an important role today. It allows us to simulate these equations. Why do we need simulations?

To analyze complex flows that don't have analytical solutions?

Exactly! Simulations help us visualize and predict fluid behaviors that would be impractical or impossible to calculate with standard methods.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The Navier-Stokes equations are crucial for solving complex fluid flow problems. Originating from the works of Claude-Louis Navier and George Stokes, these equations factor in the principles of Newtonian and non-Newtonian fluids, offering insights into momentum, pressure, and flow characteristics. The section covers the derivation process, assumptions, and the importance of boundary conditions in applying these equations.
Detailed
Introduction to Navier-Stokes Equations
The Navier-Stokes equations are pivotal in the field of fluid mechanics, underpinning many computational fluid dynamics (CFD) applications. Their historical roots trace back to physicist Claude-Louis Navier and mathematician George Stokes, who developed these equations independently. This section focuses on the derivation of the Navier-Stokes equations and highlights the assumptions associated with incompressible and isothermal flow.
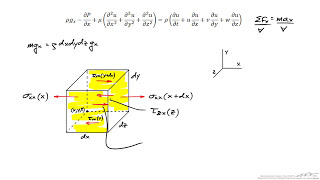
The equations emerge from the Cauchy equations which describe momentum conservation in a fluid. In simplifying this complex relationship, the equations accommodate frictional forces and density changes, providing a more manageable form for meteorological, biological, and engineering applications. The distinction between Newtonian and non-Newtonian fluids is revisited, along with how these categories affect the derivation of the equations. Throughout this process, the section emphasizes the necessity of boundary conditions and coordinate systems, as well as how these factors influence the application and understandability of the equations. Overall, the Navier-Stokes equations serve as a keystone in fluid dynamics, providing the necessary framework for analyzing and solving fluid flow problems.
Youtube Videos




![[CFD] Conservative, Advective & Material Derivative forms of the Navier-Stokes Equations](https://img.youtube.com/vi/ljdv4T2U464/mqdefault.jpg)




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Navier-Stokes Equations
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Today we are going to discuss very interesting topics, the topics on Navier-Stokes equations. They form the basic foundations of computational fluid dynamics and help solve many complex fluid flow problems.
Detailed Explanation
The Navier-Stokes equations describe how fluids move. They are fundamental to the field of fluid dynamics and are essential for understanding various fluid flow scenarios, from weather patterns to the flow of air over wings. These equations consider factors like velocity, pressure, density, and external forces acting on the fluid, providing a comprehensive description of fluid behavior.
Examples & Analogies
Think of the Navier-Stokes equations as the recipe for a complex dish, like a soufflé. Just as various ingredients and their proportions influence the final dish, factors like velocity and pressure interact to influence how a fluid will behave in various situations.
Historical Background
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Navier-Stokes equations were derived independently by French physicist Claude-Louis Navier and English mathematician George Stokes, both around 200 years ago.
Detailed Explanation
Claude-Louis Navier and George Stokes contributed significantly to fluid mechanics. Their independent work led to the derivation of the Navier-Stokes equations, allowing for the mathematical modeling of fluid motion. The collaboration of a physicist and a mathematician highlights the importance of interdisciplinary approaches in science.
Examples & Analogies
Imagine two chefs working in separate kitchens but creating very similar dishes based on the same ingredient lists. Later, they discover each other's recipes and realize that they both figured out how to achieve the same delicious outcome through different methods.
Newtonian vs. Non-Newtonian Fluids
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
I will also talk about revisiting Newtonian fluid and non-Newtonian fluid parts, which are important to look at how we can use for this Navier-Stokes equations.
Detailed Explanation
Newtonian fluids have a constant viscosity, meaning their flow behavior remains consistent regardless of the force applied to them. Examples include water and air. In contrast, non-Newtonian fluids display variable viscosity depending on the stress or rate of shear applied. A common example is ketchup, which flows easily when shaken but remains thick when left undisturbed. Understanding these differences is crucial for correctly applying the Navier-Stokes equations.
Examples & Analogies
Consider a well-mixed smoothie (Newtonian fluid) that pours smoothly compared to honey (non-Newtonian fluid), which flows slowly and requires more force to move. The transition from thick to thin flow showcases how different forces affect fluid dynamics.
Derivation of Navier-Stokes Equations
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We will talk about the derivations of Navier-Stokes equations with assumptions of incompressible isothermal flow.
Detailed Explanation
The Navier-Stokes equations can be derived by applying the principles of conservation of momentum and mass, along with the assumptions of incompressibility and constant temperature (isothermal). These assumptions greatly simplify the equations, allowing for clearer analysis of fluid dynamics. The derivation process involves breaking down forces acting on a fluid element, including pressure gradients and viscosity, leading to the final form of the equations.
Examples & Analogies
Imagine trying to understand how water flows through a garden hose. By assuming the water's temperature remains constant and that it doesn't compress under pressure, you simplify the problem. In this analogy, the simplifications help clarify how the water flows — demonstrating the value of assumptions in complex calculations.
Coordinate Systems in Navier-Stokes Equations
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We will talk about how we can form the Navier-Stokes equations in two coordinate systems – one is the Cartesian coordinate system and one is the cylindrical coordinate system.
Detailed Explanation
The Navier-Stokes equations can be expressed in different coordinate systems, such as Cartesian or cylindrical coordinates. The choice of coordinate system can simplify the equations based on the problem's geometry. For instance, cylindrical coordinates are particularly useful for problems involving rotation or symmetrical flow around a cylinder. Understanding these coordinate transformations helps in solving fluid dynamics problems more efficiently.
Examples & Analogies
Think of it like using a map to navigate. If you're traveling through the city, a street map (Cartesian coordinates) is helpful, but if you're navigating around a circular park, a park map (cylindrical coordinates) would be more effective. The right tools simplify your journey.
Application of Navier-Stokes Equations
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
After discussing the derivations, we can look at example problems with appropriate boundary conditions to solve the Navier-Stokes equations.
Detailed Explanation
Once the Navier-Stokes equations are established, applying them to real-world problems involves specifying boundary conditions — constraints that must be met within the fluid domain. For example, in a pipe flow situation, the fluid's speed at the pipe walls might be zero (no-slip condition), affecting how the equations are solved. Understanding these boundary conditions is essential for deriving meaningful and accurate solutions.
Examples & Analogies
Imagine trying to fill a balloon (the fluid domain) with air (the fluid) while ensuring it doesn’t burst. The condition that the balloon's surface must remain intact is akin to a boundary condition placed on the Navier-Stokes equations. It sets the stage for how the air (fluid) behaves inside.
Key Concepts
-
Navier-Stokes Equations: Fundamental equations governing fluid motion.
-
Incompressible Flow: Condition under which fluid density is constant.
-
Isothermal Flow: Condition where temperature remains stable during fluid motion.
-
Newtonian vs Non-Newtonian Fluids: Classification based on how viscosity behaves under stress.
-
Boundary Conditions: Crucial for determining the interaction between fluids and their environment.
Examples & Applications
Modeling airflow over a wing using the Navier-Stokes equations helps in aerodynamics design.
Simulating blood flow in arteries as a non-Newtonian fluid to better understand cardiovascular dynamics.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In fluids we’ll go, with equations aglow, Navier and Stokes showed us the flow.
Stories
Imagine a river flowing steadily—it's the Navier-Stokes equation in action, telling us how the water moves while the fish swim, unaffected by solid structures on the bank.
Memory Tools
To remember the types of fluids: N for Newtonian, N for Non-Newtonian; both adhered to by the Navier-Stokes equations.
Acronyms
NAVI
Navier-Stokes
Assumptions (incompressible
isothermal)
Viscosity types (Newtonian
Non-Newtonian)
Integrate (boundary conditions).
Flash Cards
Glossary
- NavierStokes Equations
Equations that describe the motion of viscous fluid substances, derived from the principles of conservation of momentum and mass.
- Incompressible Flow
Flow where the fluid's density remains constant.
- Isothermal Flow
Flow where the temperature of the fluid remains constant.
- Newtonian Fluid
Fluid with a constant viscosity regardless of the flow conditions.
- NonNewtonian Fluid
Fluid whose viscosity can change under stress.
- Boundary Conditions
Constraints applied to a fluid flow problem that define how the fluid interacts with surrounding boundaries.
- Cauchy Equations
Equations describing the motion of fluids based on momentum conservation.
- Computational Fluid Dynamics (CFD)
The use of numerical methods and algorithms to analyze and solve fluid flow problems.
Reference links
Supplementary resources to enhance your learning experience.
