Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Complex Eigenvectors
Unlock Audio Lesson
Today we're diving into complex eigenvectors! To start off, can anyone tell me what distinguishes complex eigenvalues from their real counterparts?
Are complex eigenvalues related to matrices that don’t have real eigenvalues?
Exactly, Student_1! Complex eigenvalues typically arise in scenarios involving oscillatory or rotational dynamics. For instance, in rotating systems, we often encounter complex eigenvalues that relate to frequency and amplitude of oscillations.
So, complex eigenvectors would be the vectors that correspond to those complex eigenvalues, right?
Precisely, Student_2! Complex eigenvectors are essential for analyzing these systems effectively. They help us to understand vibrations and dynamic behavior in structures, like turbines.
How do we know when to use complex eigenvectors instead of real ones?
Great question! If the characteristic polynomial of a matrix yields complex roots, we turn to complex eigenvectors. They are key in dynamic simulations, especially in civil engineering for structures under dynamic loads.
To sum up, complex eigenvectors arise from complex eigenvalues and are crucial for the analysis of dynamic systems.
Applications of Complex Eigenvectors
Unlock Audio Lesson
Now that we’ve covered what complex eigenvectors are, let’s discuss their applications. Why do you think they are important in civil engineering?
I believe they help in modeling how structures react under different forces, especially in rotating systems.
Exactly, Student_4! For example, in modal analysis, engineers need to account for the complex behavior of bridges under wind loads, where complex eigenvalues might emerge.
Is that why simulations often use complex eigenvectors in their analyses?
Absolutely! Software tools for dynamic simulations rely on them to model realistic behaviors of structures. The complex eigenvalues reveal information about resonance and stability.
Can you give an example of a structure that would use complex eigenvectors?
Sure! Look at wind turbines. Their dynamic responses to varying wind loads are influenced by complex eigenvectors, aiding in their design to ensure they can withstand oscillations without failing.
In summary, complex eigenvectors play a critical role in modeling dynamic systems and ensuring structural stability under varying loads.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces complex eigenvectors, emphasizing their significance in dynamic simulations and modal analysis for rotating systems, such as turbines or structures subjected to wind loads.
Detailed
Complex Eigenvectors
Complex eigenvectors are fundamental in understanding matrices with complex eigenvalues, which are particularly prevalent in dynamic systems. These eigenvectors are crucial in applications involving rotating structures, such as turbines and bridges under wind loads. When dealing with matrices whose eigenvalues are complex, it becomes essential to utilize complex eigenvectors to accurately describe the behavior of the system in dynamic analysis, ensuring that simulations and analyses reflect real-world behaviors. This aspect is pivotal in civil engineering disciplines, where understanding the dynamics of structures can influence design and safety measures.
Youtube Videos
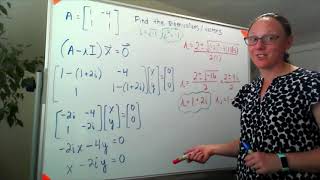
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Complex Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For matrices with complex eigenvalues (e.g., in rotating systems), eigenvectors may also be complex. These are often used in dynamic simulations and modal analysis of rotating structures like turbines or bridges under wind loads.
Detailed Explanation
This chunk introduces the concept of complex eigenvectors, which arise in matrices that have complex eigenvalues. Typically, in systems that involve rotation, such as turbines or bridges subjected to wind forces, the behavior of the system can be modeled using complex numbers. When the eigenvalues of a matrix are not real numbers, the corresponding eigenvectors may also involve complex numbers. This is crucial because these complex vectors help in describing the dynamic response of structures more accurately.
Examples & Analogies
Imagine a spinning bicycle wheel. The forces acting on the wheel and how it responds to those forces can be quite complex when in motion. Just like predicting its motion requires understanding both its position and angular momentum, understanding complex eigenvectors helps engineers predict how structures like bridges or turbines will behave under real-life dynamic conditions, especially when subjected to wind or vibrations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Complex Eigenvectors: Eigenvectors associated with complex eigenvalues, essential for dynamic analysis.
-
Dynamic Systems: Systems whose parameters evolve over time, often requiring complex eigenvector analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In modal analysis, complex eigenvectors are used to determine the stability of structures subjected to dynamic loads such as wind.
-
Turbines often use complex eigenvalue analysis to optimize their design against vibrations and fatigue.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Complex values take a whirl, in dynamic systems they twirl.
📖 Fascinating Stories
-
Imagine a sturdy bridge encountering strong winds. Engineers use complex eigenvalues to ensure it bends but doesn't break, optimizing for safety.
🧠 Other Memory Gems
-
DYNAMIC: Design Your Notable Analysis with Complex eigenvalues.
🎯 Super Acronyms
C.O.D.E
- Complex Eigenvectors Optimize Dynamic Engagement.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Complex Eigenvector
Definition:
An eigenvector associated with a complex eigenvalue, often occurring in the analysis of dynamic systems.
-
Term: Eigenvalue
Definition:
A scalar indicating how much an eigenvector is stretched or compressed during a transformation.
-
Term: Dynamic Systems
Definition:
Systems characterized by variables that change over time, essential in engineering and physics.