Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvector Decomposition
Unlock Audio Lesson
Today, we will discuss eigenvector decomposition and why it's relevant to our studies in civil engineering. Can anyone tell me what an eigenvector is?
I think an eigenvector is a special type of vector that is related to matrices.
Exactly! An eigenvector of a square matrix A satisfies the equation Ax = λx. Now, when we decompose a matrix using its eigenvectors, what do we get?
We get a way to express the matrix as products of matrices that include the eigenvalues.
That's right! We can express A as A = VDV^(-1), which simplifies analysis significantly. V contains the eigenvectors, and D contains the eigenvalues. Why do you think this is beneficial?
It makes it easier to analyze systems since we can break them down into simpler parts!
Exactly! Great summary! We can simplify complex systems of ODEs using this approach.
Applications in Civil Engineering
Unlock Audio Lesson
Now that we understand eigenvector decomposition, let's discuss how it's applied in civil engineering. Can anyone think of a context where this may be useful?
I would guess in structural vibrations?
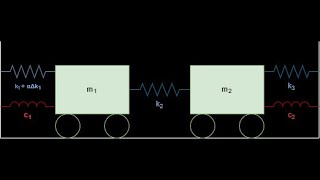
Absolutely! In analyzing the vibration modes of structures, eigenvalue problems help engineers determine how a structure behaves under dynamic loading. What do you expect to find from this analysis?
The natural frequencies and mode shapes?
Exactly! The eigenvalues give us natural frequencies, and the eigenvectors give us mode shapes. This knowledge is vital for ensuring that structures do not resonate with external forces.
Benefits of Eigenvector Decomposition
Unlock Audio Lesson
In summary, eigenvector decomposition not only simplifies complex systems but also plays a crucial role in predictions. What do you think are the major benefits we gain from using this method in engineering?
Easier calculations and clearer understanding of system behaviors?
Correct! It helps clarify how structures respond to loads. By transforming a complex issue into simpler, manageable equations, engineers can ensure safety and reliability in their designs.
Can we use this for any matrix?
Great question! Eigenvector decomposition works particularly well when the matrix has distinct eigenvectors. In cases with repeated eigenvalues, we may need generalized eigenvectors or other methods. Understanding these conditions is important for accurate analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the process of eigenvector decomposition of matrices, showcasing how matrices with linearly independent eigenvectors can be expressed in terms of their eigenvalues. The significance of this decomposition in simplifying structural analyses in civil engineering is highlighted.
Detailed
Eigenvector Decomposition of Systems
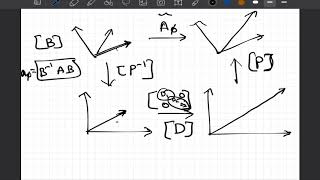
The decomposition of a matrix A with n linearly independent eigenvectors allows it to be expressed in the form:
A = VDV^{-1}
where V is the modal matrix containing the eigenvectors v1, v2,..., vn, and D is a diagonal matrix of eigenvalues λ1, λ2,..., λn. This method greatly aids civil engineers by simplifying the analysis of dynamic systems, particularly in the context of ordinary differential equations (ODEs) that describe structural vibrations. By separating complex problems into independent single-degree-of-freedom systems, engineers can better understand and predict structural behavior under various loading conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Eigenvector Decomposition Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A matrix A with n linearly independent eigenvectors v₁,...,v_n can be decomposed into:
A = VDV⁻¹
Where:
• V = [v₁,...,vₙ] is the modal matrix,
• D = diag(λ₁,...,λₙ) contains the eigenvalues.
Detailed Explanation
In this formula, we express the matrix A in terms of its eigenvectors and eigenvalues. The matrix V is created from the eigenvectors of A, where each column corresponds to one eigenvector. The matrix D is a diagonal matrix that has the eigenvalues on its diagonal. This decomposition essentially allows us to represent the original matrix A as a product of the modal matrix, the diagonal matrix of eigenvalues, and the inverse of the modal matrix. This is particularly useful because it simplifies many computations involving linear transformations.
Examples & Analogies
Think of this decomposition like a recipe where the modal matrix V represents a collection of different ingredients (eigenvectors) and the diagonal matrix D represents the exact amounts needed (eigenvalues) for the final dish (matrix A). When we mix the ingredients in the right proportions (using the inverse of V), we get the final product (matrix A). This method allows engineers to easily analyze and manipulate complex systems by breaking them down into simpler components.
Benefits in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Benefits in Civil Engineering:
• Simplifies analysis of systems of ODEs modeling structural vibration.
• Enables modal analysis, separating the problem into independent single-degree-of-freedom systems.
Detailed Explanation
In civil engineering, understanding the dynamic behavior of structures under loads such as vibrations is crucial. The eigenvector decomposition allows civil engineers to simplify complex differential equations (ODEs) that describe these vibrations. By breaking down these equations into independent parts using eigenvectors, engineers can analyze each mode of vibration separately, making calculations easier and more manageable. This leads to better predictions of how structures will respond to various loads, improving their design and safety.
Examples & Analogies
Imagine trying to understand how a large orchestra performs a symphony. Instead of analyzing the entire orchestra as a single unit, you can look at different sections, such as strings, brass, and percussion, individually. Each section (like each eigenvector) plays its own part, yet contributes to the overall performance (the structural response). By studying these sections separately, a conductor (the engineer) can identify strengths and weaknesses in the performance and make adjustments to enhance the overall sound (make the structure safer and more efficient).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector Decomposition: A method that expresses a matrix in terms of its eigenvalues and eigenvectors, facilitating simpler analysis.
-
Diagonal Matrix: A matrix containing eigenvalues along its diagonal, crucial for eigenvector decomposition.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An engineer analyzes the vibration modes of a bridge using its eigenvalues and eigenvectors to ensure structural integrity during earthquakes.
-
Eigenvector decomposition can simplify the analysis of a complex truss system by breaking it down into simpler one-dimensional systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues large, eigenvectors small, together they help us analyze all!
📖 Fascinating Stories
-
Imagine a building swaying in the wind. The architect needs to know how far it sways back and forth - eigenvectors tell how, while eigenvalues tell how strong the push is.
🧠 Other Memory Gems
-
To remember eigenvector decomposition: 'Eager Engineers Visualize Dimensions'.
🎯 Super Acronyms
EVD
- EigenVector Decomposition - a tool for simplifying matrix analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only in scale when a linear transformation is applied.
-
Term: Eigenvalue
Definition:
The scalar value that represents the factor by which an eigenvector is scaled during a linear transformation.
-
Term: Modal Matrix (V)
Definition:
A matrix where each column corresponds to an eigenvector of the original matrix.
-
Term: Diagonal Matrix (D)
Definition:
A matrix that contains eigenvalues on its main diagonal.