Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Stress and Strain
Unlock Audio Lesson
Today, we'll discuss the significance of stress and strain in materials. Stress can be represented as a tensor. Can anyone tell me what a stress tensor is?
Isn't it a mathematical representation of internal forces in a material?
Exactly! The stress tensor helps us understand how materials deform under forces. It looks like this: \( \sigma = \begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \tau_{xy} & \sigma_{yy} \end{bmatrix} \). Now, can anyone tell me what the components \( \sigma_{xx}, \tau_{xy}, \sigma_{yy} \) represent?
The components represent normal and shear stresses?
Correct! Normal stresses act perpendicular to the material, while shear stresses act parallel. Now, what do you think we need to find to understand principal stresses?
Eigenvalues?
Yes! The eigenvalue problem we use for this is \( \sigma n = \lambda n \), where \( \lambda \) gives us the principal stresses.
And the directions of these stresses are given by the eigenvectors, right?
Exactly! These principal stresses and directions are crucial in structural analysis!
Applying Eigenvalues and Eigenvectors
Unlock Audio Lesson
Now let’s dive into why knowing these eigenvalues and eigenvectors is important for engineers. How can we apply them in real-world structures?
They help determine how buildings can fail under stress, like during an earthquake!
Exactly! In earthquake engineering, we analyze the principal stresses to ensure structures can withstand tremors. Student_2, can you explain how this relates to design?
If we know the principal stresses, we can optimize material usage and ensure safety by preventing failure.
Spot on! Understanding eigenvalues and eigenvectors allows us to model stress distributions accurately, which is fundamental in civil engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
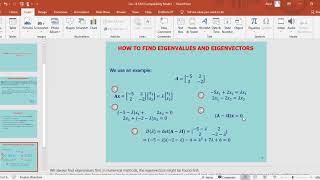
Eigenvectors are essential for finding principal stresses and principal stress directions in materials. This section describes the eigenvalue problem for determining principal stresses and stresses the significance of these concepts in the context of material strength and stability in civil engineering.
Detailed
Principal Axes and Eigenvectors
In this section, we explore eigenvectors and their critical role in understanding the principal directions of stress and strain within materials in civil engineering contexts. The stress tensor, expressed as \( \sigma = \begin{bmatrix} \sigma_{xx} & \tau_{xy} \ \tau_{xy} & \sigma_{yy} \end{bmatrix} \), is analyzed through the eigenvalue problem \( \sigma n = \lambda n \), where \( \lambda \) represents the principal stresses (eigenvalues) and \( n \) signifies the directions of those principal stresses (eigenvectors). This framework is foundational for designing and analyzing the strength of materials, soil mechanics, and concrete design, allowing engineers to predict how materials behave under various loading conditions.
Youtube Videos
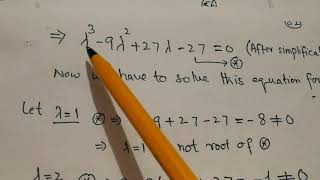
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Principal Axes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering, eigenvectors play a key role in determining the principal directions of stress and strain in materials.
Detailed Explanation
In civil engineering, understanding the principal axes is essential for analyzing how materials behave under stress. The principal axes are the directions along which the material experiences the most significant stress or strain. In technical terms, these directions are associated with the eigenvectors of the stress tensor. By identifying these axes, engineers can design structures that better withstand external forces.
Examples & Analogies
Imagine stretching a rubber band – it elongates more in the direction you are pulling it. Similarly, in materials under stress, there are specific directions (principal axes) where they experience maximum and minimum stress.
Understanding the Stress Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Stress Tensor:
σ = [ σ_xx τ_xy ]
[ τ_xy σ_yy ]
To find principal stresses and principal directions, solve the eigenvalue problem:
σn = λn
Detailed Explanation
The stress tensor is a mathematical representation that describes the stress state at a point in a material. It consists of normal stresses (like σ_xx and σ_yy, acting perpendicular to the surface) and shear stresses (like τ_xy, acting parallel to the surface). To find the principal stresses (the maximum and minimum stress values), you need to solve the eigenvalue problem associated with this tensor. Here, λ represents the principal stresses (eigenvalues), and n represents the directions where these stresses occur (eigenvectors). This conceptual framework allows engineers to assess risks and identify failure points in materials.
Examples & Analogies
Think of a thick loaf of bread. If you push down on it (applying stress), the bread compresses differently in various directions. The stress tensor helps understand how strong those compressive forces are and helps identify which parts of the loaf will squish more or break under pressure.
Applications of Principal Directions in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is foundational in strength of materials, soil mechanics, and concrete design.
Detailed Explanation
Finding the principal axes and associated stresses is vital in various engineering fields. For instance, in the design of concrete structures, engineers must ensure that the materials can withstand the principal stresses without failing. If the stresses exceed the material strength in any direction, it could lead to cracks or even catastrophic failures. Strength of materials involves managing these stresses and ensuring designs can handle the worst-case scenario. Soil mechanics applies similar principles, as understanding stress distributions in soil informs decisions on foundations and earth structures.
Examples & Analogies
Consider how a bridge design relies on understanding how weight is distributed across the deck. Engineers must calculate the principal stresses to ensure the bridge can carry the load without buckling or collapsing. Just like how a well-designed backpack can carry all your items without breaking, structures must distribute stresses effectively to be safe and functional.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector: A vector that maintains its direction during linear transformations, scaled by an eigenvalue.
-
Eigenvalue: A scalar that represents the factor by which an eigenvector is stretched or compressed.
-
Principal Stress: The maximum tension or compression experienced at a specific direction within a material.
-
Stress Tensor: A representation that encodes the state of stress at a point in a material.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a stress tensor representing a two-dimensional material and how to extract principal stresses and directions.
-
Illustration of how eigenvalues determine the principal stresses in structural analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In stress we find our forces play, Eigenvalues guide the way, Principal directions to obey, Stability's what we aim to stay.
📖 Fascinating Stories
-
Once in a land of blueprints and beams, there lived a wise engineer who spoke to her structures. She whispered, 'Tell me your secrets, where do you want to break?' And the structures responded in eigenvalues, revealing their weak points through eigenvectors that showed the way.
🧠 Other Memory Gems
-
PEE - Principal stresses are Eigenvalues, and their directions are Eigenvectors.
🎯 Super Acronyms
PES - Principal Stresses (Eigenvalues), Eigenvectors (Directions of stress).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only in scale (not direction) when a linear transformation is applied to it by a matrix.
-
Term: Eigenvalue
Definition:
The scalar that indicates how much an eigenvector is stretched or compressed during a linear transformation.
-
Term: Principal Stress
Definition:
The maximum or minimum normal stress at a point in an object, occurring in the principal directions where shear stress is zero.
-
Term: Stress Tensor
Definition:
A mathematical representation that describes the internal stress state of a material, represented in a matrix form.