Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvectors in Structural Analysis
Unlock Audio Lesson
Today, we're going to explore how eigenvectors are utilized in structural analysis. Can anyone tell me what an eigenvector is?
Isn't it a vector that doesn't change direction in a linear transformation?
Exactly, Student_1! In the context of structural analysis, eigenvectors represent mode shapes of vibration. For example, when a building is subjected to forces, we can use eigenvectors to predict how it will sway.
So, how does this help in engineering?
Great question, Student_2! By knowing the mode shapes, engineers can see where stress points may occur and prevent potential failures. We can remember this use with the acronym 'M.S.P.': Mode Shapes Predict.
Dynamic Loading and Structural Response
Unlock Audio Lesson
When discussing structural analysis, we also need to consider dynamic loading—like during an earthquake. Student_3, what could happen if a structure isn’t well designed for these loads?
It could collapse or suffer severe damage!
Yes! That’s why analyzing eigenvectors helps engineers devise strategies for reinforcing structures. Let's recall that eigenvectors give us insight into the distribution of forces during these events.
Is there a practical example of this?
Absolutely! Consider a tall building swaying during a storm. Engineers can model this using eigenvectors to ensure the building remains stable. So think of eigenvectors as the guideposts for safe structural design in turbulent conditions.
Real-World Applications of Eigenvectors in Engineering
Unlock Audio Lesson
Now, let’s look at real-world applications of eigenvectors in engineering. Student_2, can you think of a structure that may significantly benefit from eigenvector analysis?
Bridges! They have to deal with a lot of different forces.
Exactly! Bridges are subjected to various loads, including vehicles and wind. Engineers use eigenvectors to ensure that the structure can safely support these dynamic forces through modal analysis.
So they prevent collapse through these calculations?
Right! Remember: M.S.P. stands for 'Mode Shapes Predict'—they predict how structures will act under different conditions, fostering safety.
Challenges in Structural Engineering
Unlock Audio Lesson
Finally, let's address some challenges in applying eigenvector analysis. Student_4, what might be a limitation?
If the models are too simplistic, they might miss important factors?
Exactly! Simplistic models can overlook complexities like material fatigue. Engineers must constantly refine their analyses to account for real-world variables. It's crucial to adapt and evolve our understanding as structures face different stresses.
So continual learning and adaptation are key?
Yes! Remember, engineering is not just about calculations; it's about understanding and adapting. Keep the M.S.P. principle in mind. As structures evolve, so too should our methods.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvectors are crucial in structural analysis as they represent mode shapes of vibration and deformation in structures. The section outlines how engineers use these vectors to predict structural responses under dynamic loads, contributing significantly to the design process for safety and stability.
Detailed
Structural Analysis
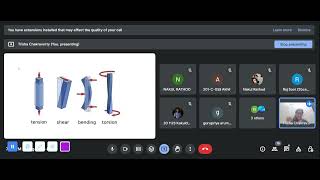
In civil engineering, structural analysis is essential for understanding how structures respond to various forces. Eigenvectors serve a critical role here, particularly in analyzing how structures vibrate or deform under load. By determining the 'mode shapes' of a structure through eigenvectors, engineers can forecast potential failure points under dynamic loading conditions. This section notes that eigenvectors help indicate how different parts of a structure will move relative to one another when influenced by forces such as earthquakes or wind. Engineers rely on these calculations to create resilient designs that will withstand real-world challenges.
Youtube Videos
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector: A vector that signifies a direction in which a linear transformation acts by simply stretching or compressing.
-
Mode Shape: The specific way a structure deforms during vibration, which helps predict responses under dynamic loads.
-
Dynamic Loading: Loads that change over time, crucial to understanding real-world structural responses.
-
Structural Analysis: The process of evaluating structures to ensure they can withstand the forces they encounter.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a skyscraper designed to sway minimally under high winds, incorporating eigenvector analysis to determine safe vibrations.
-
Example of a bridge analyzed using eigenvectors to ensure it can support vehicle loads without collapsing.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In structural beams that sway, eigenvectors show the way,
📖 Fascinating Stories
-
Imagine a tall building in a storm, swaying gently with its form. Thanks to eigenvectors, it knows just how to bend, ensuring safety from beginning to end.
🧠 Other Memory Gems
-
M.S.P.: Mode Shapes Predict - remember that eigenvectors forecast structural behavior!
🎯 Super Acronyms
D.L. for Dynamic Loading - think of all the forces that change and sway, such as storms and shifty play.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that changes by a scalar factor when a linear transformation is applied.
-
Term: Mode Shape
Definition:
The specific pattern of motion that a structure undergoes during vibration.
-
Term: Dynamic Loading
Definition:
Loads that vary with time, influencing the response of a structure, such as wind or earthquakes.
-
Term: Structural Analysis
Definition:
The study of how structures respond to various forces and loads.