Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Linearly Independent Eigenvectors
Unlock Audio Lesson
Today, we will explore the property that if a matrix A has n distinct eigenvalues, its corresponding eigenvectors are linearly independent. This means no eigenvector can be written as a combination of the others.
What does it mean for eigenvectors to be linearly independent?
Good question! Linear independence means that if you try to express one eigenvector as a combination of the others, you won't be able to do it unless all coefficients are zero.
Can you give an example showing why this is important?
Absolutely! If we have three eigenvectors corresponding to three distinct eigenvalues, it gives us a complete basis in R³, allowing us to express any vector in that space using these eigenvectors.
Oh, so it helps span the space!
Exactly! That’s a key takeaway. To remember this: think 'Distinct means Different Directions!'
Scaling of Eigenvectors
Unlock Audio Lesson
Now let's discuss the scaling property of eigenvectors. If x is an eigenvector, then kx is also an eigenvector for any non-zero scalar k.
That sounds intuitive, but why is that the case?
When we say Ax = λx, if we multiply both sides by k, we get A(kx) = kλx, which shows kx satisfies the eigenvalue equation with the same eigenvalue λ.
So, does that mean that there are infinitely many eigenvectors?
Precisely! This scaling leads to an entire line of eigenvectors in the direction of x. You can always visualize it as stretching or compressing that vector.
That's like saying every eigenvector multiplied by a number is still on the same line!
Exactly! A memory aid here can be, 'Scale to Trail!' Each eigenvector creates a trail of its scaled versions.
Diagonalization of Matrices
Unlock Audio Lesson
Next, let's discuss diagonalization. A matrix A is diagonalizable if it has n linearly independent eigenvectors. Can anyone tell me what that allows us to do?
Does it make calculating high powers of matrices easier?
Exactly right! We can express A as A = PDP⁻¹, where D is a diagonal matrix of eigenvalues. This simplifies computations significantly.
What’s a real-world application of this?
One application is in simulations. Diagonalizing a matrix means we can quickly compute power systems in engineering problems.! Always remember: 'Diagonalization = Simplification!'
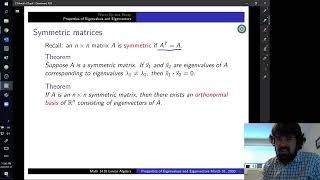
Eigenvectors of Symmetric Matrices
Unlock Audio Lesson
Let's look at symmetric matrices. All eigenvalues of a real symmetric matrix are real, and eigenvectors corresponding to distinct eigenvalues are orthogonal. Why is this interesting?
Orthogonal means they don’t overlap in a sense?
Exactly! It means the dot product of those eigenvectors is zero, making them very useful in applications like modal analysis.
How do we prove that they are orthogonal?
For distinct eigenvalues, you can show that if Ax = λx and Ay = μy, then from the symmetry of the matrix, two eigenvectors x and y corresponding to distinct eigenvalues λ and μ are orthogonal. We can leverage these properties in structural mechanics. Remember, 'Distinct Equals Orthogonal!'
Review of Properties
Unlock Audio Lesson
To wrap up, we discussed four key properties of eigenvectors. Can anyone summarize them for me?
Sure! There are linearly independent eigenvectors for distinct eigenvalues, eigenvectors can be scaled, a matrix can be diagonalized if it has enough independent eigenvectors, and symmetric matrices have real eigenvalues with orthogonal eigenvectors.
Excellent! And remember: 'Independent, Scalable, Diagonalizable, and Orthogonal!' This will help you remember the essential properties of eigenvectors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The properties of eigenvectors play a crucial role in understanding their behavior in linear algebra. Key aspects include the linear independence of eigenvectors associated with distinct eigenvalues, the scalability of eigenvectors, the conditions for diagonalizability, and the orthogonal nature of eigenvectors in symmetric matrices.
Detailed
Properties of Eigenvectors
Eigenvectors are essential in the analysis of linear transformations. This section discusses four primary properties:
- Linearly Independent Eigenvectors: If matrix A has n distinct eigenvalues, it guarantees that the corresponding eigenvectors are linearly independent. This is significant because it implies that these eigenvectors can span the vector space.
- Scaling: Eigenvectors are not unique; for example, if x is an eigenvector, then kx (where k is any non-zero scalar) is also an eigenvector. This highlights that eigenvectors can be multiplied by a scalar without losing their property.
- Diagonalization: A matrix A can be diagonalized if it has n linearly independent eigenvectors. In such cases, A can be expressed as a product of matrices: A = PDP⁻¹, where D is a diagonal matrix containing the eigenvalues, and P consists of the eigenvectors. Diagonalization simplifies the process of raising matrices to powers.
- Symmetric Matrices: For real symmetric matrices, eigenvalues are real numbers, and eigenvectors corresponding to distinct eigenvalues will be orthogonal to each other. This orthogonality is especially notable in applications like modal analysis, where it facilitates calculations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Linearly Independent Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If matrix A has n distinct eigenvalues, the corresponding eigenvectors are linearly independent.
Detailed Explanation
This statement means that each eigenvector associated with distinct eigenvalues cannot be formed by taking a linear combination of the others. In simpler terms, if you have a square matrix A that produces n different eigenvalues, then the eigenvectors connected to those eigenvalues do not overlap or align in a way that one can be represented using the others. This property is critical because it ensures the eigenvectors form a basis for the space, which is essential in various applications including stability analysis and structural engineering.
Examples & Analogies
Imagine you have several unique colors of paint: red, blue, and yellow. Each pure color can stand on its own and cannot be created by mixing the others. Similarly, each eigenvector for a matrix with distinct eigenvalues stands alone, providing a unique direction in the vector space.
Scaling of Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eigenvectors are not unique. If x is an eigenvector, so is kx for any non-zero scalar k.
Detailed Explanation
This property highlights that eigenvectors can be scaled by any non-zero factor and still remain valid eigenvectors. For instance, if x is an eigenvector corresponding to a certain eigenvalue, then multiplying it by 2 (or any other non-zero scalar) will still produce a valid eigenvector with the same direction but changed magnitude. This concept is important because it allows flexibility in selecting eigenvectors, as any scalar multiple can be used without loss of generality.
Examples & Analogies
Think about a direction on a map. You can express the same direction by saying 'go 5 miles northeast' or 'go 10 miles northeast'. Both directions point to the same trajectory; they just differ in distance. Similarly, any non-zero scalar multiple of an eigenvector points in the same direction.
Diagonalization of Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If A has n linearly independent eigenvectors, then it is diagonalizable: A=PDP^{-1} where D is a diagonal matrix with eigenvalues, P is a matrix whose columns are the eigenvectors of A.
Detailed Explanation
Diagonalization is a process that simplifies a square matrix into a diagonal form using its eigenvectors. If there are n linearly independent eigenvectors for an n x n matrix A, it can be expressed in a diagonal form A=PDP^{-1}. Here, D contains eigenvalues along its diagonal, while P is constructed from the eigenvectors. This simplification allows for easier computation in applications like solving systems of linear equations, as working with a diagonal matrix is less complex than with a full matrix.
Examples & Analogies
Consider organizing a group of people by their heights; placing the tallest on one side and the shortest on the other creates a clear, organized line. Diagonalization does something similar for matrices: it organizes the components (eigenvalues and eigenvectors) in a way that makes calculations straightforward.
Properties of Symmetric Matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
All eigenvalues of a real symmetric matrix are real, and eigenvectors corresponding to distinct eigenvalues are orthogonal.
Detailed Explanation
This property refers to how eigenvalues behave when dealing with symmetric matrices (where the matrix is equal to its transpose). All eigenvalues will be real (not complex), which is a powerful feature in real-world applications. Additionally, eigenvectors associated with different eigenvalues are orthogonal, meaning they are at right angles to each other. This orthogonality simplifies many mathematical operations, making calculations involving projections and transformations much more convenient.
Examples & Analogies
Think of two musicians playing different instruments. Their sound can be heard distinctly when they play in different areas, making them orthogonal. Similarly, distinct eigenvectors maintain their identity and do not overlap, simplifying the 'sound' of calculations in solving equations involving symmetric matrices.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linearly Independent Eigenvectors: If a matrix has n distinct eigenvalues, its eigenvectors are linearly independent.
-
Non-Unique Eigenvectors: Eigenvectors can be scaled by any non-zero scalar.
-
Diagonalization: A matrix with n linearly independent eigenvectors can be diagonalized.
-
Symmetric Matrices: Eigenvalues are real, and corresponding eigenvectors for distinct eigenvalues are orthogonal.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix with distinct eigenvalues, the eigenvectors span the space, showing their importance in linear algebra.
-
In symmetric matrices, eigenvalues are guaranteed to be real, and each corresponding eigenvector is orthogonal to others with different eigenvalues.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Eigenvalues are real for matrices that are symmetric, scaling eigenvectors means true here, it's terrific!
📖 Fascinating Stories
-
Imagine eigenvectors as people standing in a line. Each has their unique height, and if they stand tall or shrink, they still can guide you in the right direction - just like eigenvectors, where scaling maintains their alignment.
🧠 Other Memory Gems
-
Remember 'S.L.O.' for properties: Scaling, Linearly independent, Orthogonality.
🎯 Super Acronyms
Use 'D.S.O.' to remember
- Diagonalization
- Scaling
- and Orthogonality of eigenvectors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvalues
Definition:
Scalars that measure the factor by which an eigenvector is stretched or compressed during a linear transformation.
-
Term: Eigenvectors
Definition:
Non-zero vectors that, when multiplied by a matrix, yield a scalar multiple of itself.
-
Term: Diagonalize
Definition:
The process of transforming a matrix into a diagonal form using its eigenvectors.
-
Term: Symmetric Matrix
Definition:
A matrix that is equal to its transpose, having real eigenvalues and orthogonal eigenvectors.
-
Term: Linearly Independent
Definition:
A set of vectors that do not linearly combine to produce the zero vector.