Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Eigenvalues and Eigenvectors
Unlock Audio Lesson
Today, we'll learn how to find eigenvectors once we have the eigenvalues. Can anyone remind me what an eigenvalue is?
An eigenvalue is a scalar that indicates how much an eigenvector is stretched or compressed.
Correct! Now, if we have a matrix A and its eigenvalue λ, how do we find the corresponding eigenvector?
We set up the equation (A - λI)x = 0, right?
Exactly! This leads us to a system of equations. What does it mean if a solution is non-trivial?
It means there are solutions other than the zero vector.
Exactly! Let's summarize: eigenvalues indicate scaling and we use the equation (A - λI)x = 0 to find non-zero eigenvectors.
Example Calculation of Eigenvector
Unlock Audio Lesson
Now, let's apply what we've learned using the matrix A = [[4, 2], [1, 3]]. What’s our first step?
We need to find the eigenvalues first by determining the characteristic equation.
Correct! What does the characteristic equation look like?
det(A - λI) = 0!
Great! What do we get when we calculate that for matrix A?
We end up with λ² - 7λ + 10 = 0, yielding eigenvalues λ=5 and λ=2.
Perfect! Now, how do we find the eigenvector related to λ=5?
We set up (A - 5I)x = 0 and solve the resulting equations.
Exactly! What do we find as our eigenvector?
The eigenvector is proportional to (2, 1).
Excellent! So remember: after finding eigenvalues, we can derive eigenvectors by solving (A - λI)x = 0. Let's summarize what we've learned today.
Significance and Application of Eigenvectors
Unlock Audio Lesson
Next, let's discuss why learning to find eigenvectors is essential. Can anyone think of an application in civil engineering?
In vibration analysis, eigenvectors help determine how structures respond to loads.
Exactly! Eigenvectors can show mode shapes of structures during vibrations. Why is understanding these shapes important?
They help ensure that structures do not resonate and fail during events like earthquakes.
Correct! Remember, eigenvectors simplify complex systems into manageable analyses. Let's summarize the importance of eigenvectors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the procedure for finding eigenvectors of a matrix is discussed, focusing on solving the homogeneous linear equations derived from the characteristic equation. An example with a specific matrix illustrates the steps taken to find eigenvectors, emphasizing the importance of techniques like Gaussian elimination.
Detailed
Finding Eigenvectors
Finding eigenvectors is a crucial step in linear algebra and has significant applications in engineering, particularly in the context of system stability and vibrations. Once the eigenvalues of a square matrix are identified, the corresponding eigenvectors can be derived from the equation
$$ (A - \lambda I)x = 0 $$
This equation represents a homogeneous system of linear equations. To solve for the eigenvector, we set up a matrix formed by substituting the eigenvalue into the equation. By using methods such as Gaussian elimination or row-reduction, one can find the eigenvector, usually defined up to a scalar multiple. The significance of this is in understanding the action of transformations based on the eigenvectors, which geometrically represent directions in which linear transformations merely stretch, compress, or reverse vectors without altering their directions. An illustrative example involves finding eigenvectors for a specific matrix, showcasing the step-by-step process and underlying principles.
Youtube Videos
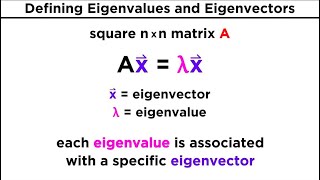
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Finding Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once the eigenvalues λᵢ are found, each corresponding eigenvector x can be obtained by solving:
(A−λᵢ I)x = 0
Detailed Explanation
After determining the eigenvalues of a matrix, the next step is to calculate the eigenvectors. This is done by substituting each eigenvalue into the equation (A−λᵢ I)x = 0, where A is the original matrix, λᵢ is the eigenvalue, and I is the identity matrix. The goal is to find the vector x that satisfies this equation.
Examples & Analogies
Think of eigenvectors as specific directions or paths that maintain their identity (or direction) when influenced by the matrix (like a wind blowing in a consistent direction). For instance, if you imagine a person walking along a path (the eigenvector) while a strong wind (the matrix) may change their speed without changing the direction they walk, this illustrates how eigenvectors behave under transformations.
Solving for Eigenvectors Using Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This typically results in a system of linear equations, which can be solved using Gaussian elimination or row-reduction.
Detailed Explanation
The equation (A−λᵢ I)x = 0 leads to a set of linear equations. Solving these equations can be achieved through methods like Gaussian elimination, where one transforms the system into a simpler form to find the solutions for x. This process is essential to discover the eigenvectors for each eigenvalue.
Examples & Analogies
Imagine you're solving a mystery with clues (equations). Each clue leads you closer to understanding the story (finding the eigenvector). Just like using a map to navigate to a destination, methods like Gaussian elimination guide you step-by-step to uncover the solutions needed to find those special paths (eigenvectors).
Example of Finding Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example: Let A = [4 2; 1 3]
Step 1: Find characteristic equation
det(A−λI) = |(4−λ)(3−λ)−2| = λ²−7λ+10⇒λ²−7λ+10 = 0 ⇒ λ = 5, 2
Step 2: Find eigenvectors
For λ=5: (A−5I)x = 0 ⇒ Solve -x + 2y = 0 ⇒ x = 2y
Eigenvector x = [2; 1] (up to scalar multiple)
Detailed Explanation
In this example, we first determine the eigenvalues for matrix A. After calculating the determinant and solving the characteristic equation, we find two eigenvalues, 5 and 2. Next, we substitute each eigenvalue back into the equation (A−λᵢ I)x = 0 to derive the corresponding eigenvectors. For λ = 5, we obtain a simple linear equation (-x + 2y = 0) leading us to find the eigenvector [2; 1]. This demonstrates the practical steps involved in finding eigenvectors.
Examples & Analogies
Think of the matrix as a recipe book and the eigenvalues as specific recipes you want to make. Each recipe has unique ingredients (eigenvectors) that give the dish its character. In our example, by first figuring out which recipes (eigenvalues) you want to cook and then gathering the necessary ingredients (eigenvectors), you effectively create the dishes (solutions) that showcase unique flavors (characteristics) tied to each recipe.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvector: A vector associated with an eigenvalue that represents a direction of a transformation.
-
Eigenvalue: A scalar that indicates the factor by which an eigenvector is stretched or compressed.
-
Characteristic Equation: The equation used to find eigenvalues, derived from the determinant of (A - λI).
-
Solution of Eigenvector: Found by resolving the equation (A - λI)x = 0.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For matrix A = [[4, 2], [1, 3]], the eigenvalues are λ=5 and λ=2. The eigenvector corresponding to λ=5 is (2, 1).
-
In civil engineering, eigenvectors help model structures under dynamic loads, determining how they will deform.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Finding eigenvectors is quite nifty, solve (A-λI)x, things get shifty.
📖 Fascinating Stories
-
Imagine a designer analyzing bridges. They compute eigenvalues, then visualize how the structures sway with eigenvectors, ensuring safety in storms.
🧠 Other Memory Gems
-
Remember "EIG Vap" for Eigenvalue and Eigenvector search: Eigenvalue, Identify (matrix), Gaussian elimination (to solve), Vector.
🎯 Super Acronyms
EVE - Eigenvalue, Vector, Eigenvector.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that is only scaled by a transformation, specified by a matrix.
-
Term: Eigenvalue
Definition:
A scalar that indicates how much an eigenvector is stretched or compressed by a transformation.
-
Term: Homogeneous System
Definition:
A system of linear equations set to zero, where at least one solution is non-trivial.
-
Term: Matrix A
Definition:
A square array of numbers used for linear transformations.
-
Term: Gaussian Elimination
Definition:
A method for solving systems of linear equations using row operations.