Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Characteristic Equation
Unlock Audio Lesson
Today, we'll explore how to find eigenvalues using the characteristic equation derived from a square matrix. Can anyone remind me what we typically look for in a matrix to find an eigenvalue?
Is it the scalar that stretches or compresses the eigenvector?
Exactly! The eigenvalue is that scalar. Now, to find it, we start with the equation Ax = λx. How do we transform this to find our characteristic equation?
We rearrange to (A−λI)x = 0, right?
Correct! By setting A−λI to zero, we create the characteristic equation. What do we do next with it?
We need to find the determinant and set it to zero!
Yes! When we compute the determinant of (A−λI) and set it to zero, we can find the eigenvalues. Let’s remember that this is a crucial step known as obtaining the characteristic equation.
Finding Eigenvectors from Eigenvalues
Unlock Audio Lesson
Now that we have our eigenvalues, who can tell me the next step for finding the corresponding eigenvectors?
We use the equation (A−λI)x = 0 for each eigenvalue, right?
Very good! After finding each eigenvalue λᵢ, we plug it back into the equation. What are we looking for?
We’re looking for the non-zero vector x that satisfies the equation.
Exactly! This will yield a homogeneous system of equations. Does anyone know a method we could use to solve these equations?
We could use Gaussian elimination or row reduction.
Right on! Solving these will help us determine the eigenvectors corresponding to each eigenvalue. Remember, these eigenvectors can also be scaled, meaning there are infinitely many that correspond to an eigenvalue.
Significance of Eigenvalues and Eigenvectors
Unlock Audio Lesson
Let’s shift gears. Can anyone share why eigenvalues and eigenvectors are significant in engineering?
They help in understanding vibrations in structures!
Absolutely! They provide insights into mode shapes and natural frequencies in structural dynamics. How about in stability studies?
Eigenvalues give critical loads associated with buckling in columns!
Exactly! By solving the eigenvalue problem, engineers can predict potential failure modes. Remember, this method is vital in software tools used for civil engineering analysis.
It's amazing how math helps in real-world applications!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains how to find eigenvalues and eigenvectors by solving the characteristic equation of a square matrix. It emphasizes the importance of the determinant and introduces the notation associated with eigenvalues and eigenvectors.
Detailed
Eigenvalue Problem
To determine the eigenvalues and eigenvectors of a square matrix A, we solve the characteristic equation derived from the equation Ax = λx. The transformation leads us to a homogeneous system of linear equations represented as (A−λI)x = 0, where the matrix A must be singular (i.e., its determinant must equal zero) for non-trivial solutions to exist. This condition generates the characteristic equation, denoted as det(A−λI) = 0, whose roots yield eigenvalues λ₁, λ₂, ..., λₙ. Once the eigenvalues are identified, eigenvectors corresponding to each eigenvalue can be computed by solving the system (A−λI)x = 0. This foundational concept is crucial in applications across various engineering fields, particularly in modeling and analyzing physical systems.
Youtube Videos
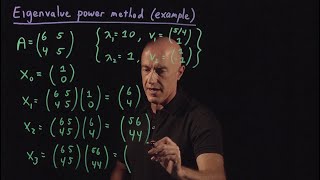
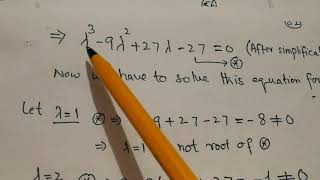
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Characteristic Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To find eigenvectors, we start by solving the characteristic equation:
Ax=λx⇒(A−λI)x=0
This is a homogeneous system of equations, and for a non-trivial solution to exist (i.e., x̸=0), the coefficient matrix must be singular:
det(A−λI)=0
Detailed Explanation
The characteristic equation is foundational in finding eigenvalues and eigenvectors. We start with the equation Ax = λx, where A is the square matrix, x is the eigenvector, and λ is the eigenvalue. Rearranging gives (A - λI)x = 0, indicating a system of linear equations. To find solutions for x (the eigenvectors), we need this system to have a non-trivial solution, meaning the solution cannot be the zero vector. For this to happen, the determinant of the matrix A - λI must equal zero (det(A - λI) = 0). This condition determines the eigenvalues (λ) of the matrix A.
Examples & Analogies
Think of a bridge. To understand how much weight it can support (which can change with different loads), engineers need to analyze its structure using mathematical models. The characteristic equation helps in determining the 'strength' of the bridge under various conditions, much like how eigenvalues help predict stability under stress.
Characteristic Equation and Eigenvalues
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This equation is called the characteristic equation, and its roots λ1, λ2, ..., λn are the eigenvalues of A.
Detailed Explanation
The characteristic equation stems from the condition det(A - λI) = 0. When we solve this polynomial equation, we find its roots, which are the eigenvalues of the matrix A. Each eigenvalue corresponds to an eigenvector that reveals how that eigenvalue scales the matrix's transformations on vectors in its space.
Examples & Analogies
Consider an elevator in a tall building. The eigenvalues can be seen as the different weights the elevator can carry safely without malfunctioning. Just like understanding the limits (eigenvalues) helps in ensuring safety and performance, knowing eigenvectors helps understand how the system behaves when subjected to those weights.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalue Problem: A mathematical approach to finding eigenvalues and eigenvectors from a given matrix.
-
Characteristic Equation: The determinant of (A−λI) set to zero; used to find eigenvalues.
-
Eigenvectors: Vectors that remain on the same line when a transformation is applied, scaled by eigenvalues.
-
Non-trivial Solutions: Solutions to equations that are not just zero; crucial for determining eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a matrix A = [[4, 2], [1, 3]], the characteristic equation det(A−λI) is derived, yielding eigenvalues λ = 5, 2.
-
For eigenvalue λ = 5, solving (A−5I)x = 0 leads to the eigenvector x = [2, 1].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For eigenvalues we seek, a determinant so weak, sets the matrix to sway, eigenvectors on display.
📖 Fascinating Stories
-
Imagine a square matrix, lonely on a blank page, needing to find its way. By exploring its characteristic equation, it discovers eigenvectors leading the way through transformations—strengthening its existence!
🧠 Other Memory Gems
-
DREAM - Determinant Zero, Roots of Eigenvalues, Eigenvectors Found, Apply Transformation, Matrix Singularity.
🎯 Super Acronyms
ACE - A characteristic equation gives eigenvalues and eigenvectors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only by a scalar factor when a linear transformation is applied.
-
Term: Eigenvalue
Definition:
A scalar associated with an eigenvector that indicates how much the eigenvector is stretched or compressed.
-
Term: Characteristic Equation
Definition:
An equation obtained from det(A−λI) = 0 used to find the eigenvalues of a matrix.
-
Term: Determinant
Definition:
A scalar value that describes certain properties of a matrix, including whether it's invertible.
-
Term: Homogeneous System
Definition:
A system of equations that is equal to zero.