Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvectors
Unlock Audio Lesson
Today, we're going to dive into the world of eigenvectors. Can anyone tell me what an eigenvector is?
Isn't it a special vector that comes from a matrix?
Exactly! An eigenvector is a non-zero vector that changes its scale but not its direction when multiplied by a matrix. What about the corresponding eigenvalue?
The eigenvalue is a scalar that indicates how much the eigenvector is stretched or compressed?
Right! We can remember this relationship with the acronym 'SCALE' – Stretch, Compress, And Leave direction unchanged. Next, let's discuss the characteristic equation. Who can explain what it is?
Isn't it det(A - λI) = 0?
That's correct! The roots of the characteristic equation give us the eigenvalues.
And then we can find the eigenvectors from that?
Exactly! To summarize, we have a definition of eigenvectors, the role of eigenvalues, and how we find them together.
Finding Eigenvectors
Unlock Audio Lesson
Now that we understand eigenvalues, let's look at a specific example. If we have a matrix A, how would we find its eigenvalues?
We'd calculate the determinant of (A - λI) and set it to zero, right?
Correct! Let's say our matrix A is [[4, 2], [1, 3]]. What would the determinant look like?
It would be (4 - λ)(3 - λ) - 2!
Right! And if we solve that, we get the eigenvalues λ = 5 and λ = 2. Now, let's find the eigenvectors. Who would like to give it a try?
For λ = 5, we solve (A - 5I)x = 0, which ends up giving us the vector form.
Excellent! So you've derived that eigenvector corresponds to the eigenvalue. Let's summarize our key steps: finding the characteristic polynomial and extracting eigenvectors.
Application of Eigenvectors
Unlock Audio Lesson
Moving on, let's discuss how we actually use eigenvectors in engineering. Can anyone think of a practical application?
I think they're used in structural analysis, right?
Exactly! In structural analysis, we determine the mode shapes using eigenvectors to understand how structures respond to loads. Can anyone elaborate further?
They also help with vibration analysis to prevent resonance in structures, don't they?
Absolutely! Eigenvalues indicate the natural frequencies of vibration. Remember the acronym 'MODES' – Modes of deformation, Own shapes of vibration, Dynamics understanding, Engineering applications, and Structural failure prevention.
That makes it clearer why eigenvectors are crucial! They connect theory with real-world applications.
Yes! To wrap up, eigenvectors give us powerful insight into understanding complex engineering systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Eigenvectors are non-zero vectors associated with a square matrix that, when transformed by the matrix, result in a scalar multiple of themselves. This section explores their mathematical foundations, properties, and applications in fields such as structural analysis and vibration analysis, providing engineers with tools to model various physical phenomena.
Detailed
Eigenvectors
Eigenvectors are essential in understanding linear transformations and play a crucial role in systems of linear equations. Defined for a square matrix A, an eigenvector x (where x ≠ 0) satisfies the equation Ax = λx, where λ is the eigenvalue corresponding to x. This relationship signifies that the transformation represented by matrix A scales vector x by the factor λ, preserving its direction. The identification of eigenvectors begins with solving the characteristic polynomial obtained from det(A - λI) = 0, where roots yield the eigenvalues. The corresponding eigenvectors can be found through substitution into the equation (A − λI)x = 0. Key properties include linear independence, non-uniqueness (scaling), and diagonalizability when a matrix possesses distinct eigenvalues. In civil engineering, eigenvectors are heavily utilized in applications such as structural analysis, vibration analysis, and stability studies.
Youtube Videos
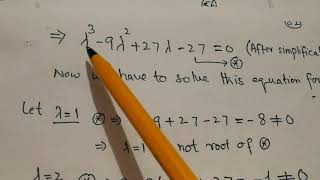
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eigenvectors are fundamental in the study of linear transformations and systems of linear equations. In civil engineering, they are widely used in structural analysis, vibration analysis, stability studies, and finite element methods. Understanding eigenvectors and the corresponding eigenvalues helps civil engineers model physical phenomena such as resonance, stress distribution, and buckling of columns.
Detailed Explanation
Eigenvectors are important concepts in linear algebra, particularly when dealing with matrices. They allow engineers to analyze and predict how structures will react under various forces. In civil engineering, eigenvectors can help determine how structures vibrate and distribute stresses. For example, when a building sways during an earthquake, eigenvectors help calculate how the building's materials will respond to the shaking, ensuring that the structure remains stable and safe.
Examples & Analogies
Think of a swing at a playground. When you push it, it swings back and forth, and this motion has a specific rhythm or pattern. In a similar way, buildings have 'natural' ways of moving when forces are applied to them, and eigenvectors help identify those movements, much like understanding the rhythm of the swing helps you know how far to push it without going too high.
Definition of Eigenvector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An eigenvector x≠0 of matrix A is a non-zero vector that, when multiplied by the matrix A, yields a scalar multiple of itself: Ax=λx. Here, • x is the eigenvector, • λ∈R (or C) is the eigenvalue associated with x, • A is a square matrix.
Detailed Explanation
An eigenvector is a special type of vector that, when acted upon by a square matrix A, does not change its direction; it only gets scaled (stretched or compressed). The scalar by which it is scaled is known as the eigenvalue (λ). Mathematically, this relationship can be expressed as Ax = λx. In this equation, A transforms the eigenvector x into another vector, but this new vector points in the same direction as the original one, just altered in length.
Examples & Analogies
Imagine you have a rubber band (the eigenvector) that you pull (the matrix A). When you stretch the rubber band, it becomes longer (scaled), but it remains in the same direction no matter how much you pull. The amount by which you stretch it is similar to the eigenvalue. If you pull the rubber band lightly, it extends a little (small eigenvalue). If you pull it hard, it extends a lot (large eigenvalue).
The Eigenvalue Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To find eigenvectors, we start by solving the characteristic equation: Ax=λx⇒(A−λI)x=0. This is a homogeneous system of equations, and for a non-trivial solution to exist (i.e., x≠0), the coefficient matrix must be singular: det(A−λI)=0.
Detailed Explanation
The eigenvalue problem involves finding both eigenvalues and eigenvectors of a matrix A. We solve for these by first transforming the equation into a characteristic form, (A − λI)x = 0, where I is the identity matrix. This transformation allows us to find values for λ that tell us what the eigenvalues are. To determine the eigenvalues of the matrix, we compute the determinant of (A − λI) and set it equal to zero. The solutions (roots) of this equation are the eigenvalues, which further allow us to find the corresponding eigenvectors.
Examples & Analogies
Imagine you are tuning a musical instrument, like a guitar. Each string can vibrate at certain frequencies (eigenvalues), and those frequencies correspond to specific notes. The way a string vibrates along its length is akin to its eigenvector. To find out which notes (eigenvalues) your guitar strings can produce, you may pluck the strings and observe their vibrations, just as we solve the characteristic equation to find eigenvalues.
Finding Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once the eigenvalues λ are found, each corresponding eigenvector x can be obtained by solving: (A−λI)x=0. This typically results in a system of linear equations, which can be solved using Gaussian elimination or row-reduction.
Detailed Explanation
After calculating eigenvalues, the next step is to find eigenvectors for each eigenvalue. This involves substituting each eigenvalue into the equation (A − λI)x = 0. The result is a linear system of equations which can be resolved using techniques like Gaussian elimination or row-reduction, resulting in the eigenvectors that correspond to each eigenvalue. Each eigenvector indicates a direction in which the matrix transformation only scales the vector without altering its direction.
Examples & Analogies
Think of this process like fitting different puzzle pieces (eigenvectors) into a puzzle board (the matrix). Each piece fits perfectly in a specific orientation that highlights its unique shape (its eigenvalue). Once you know a piece's orientation based on its characteristics (its eigenvalue), you can find how it fits in the larger puzzle, allowing you to see the bigger picture of how everything connects.
Properties of Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Linearly Independent Eigenvectors: If matrix A has n distinct eigenvalues, the corresponding eigenvectors are linearly independent.
- Scaling: Eigenvectors are not unique. If x is an eigenvector, so is kx for any non-zero scalar k.
- Diagonalization: If A has n linearly independent eigenvectors, then it is diagonalizable: A=PDP⁻¹.
- Symmetric Matrices: All eigenvalues of a real symmetric matrix are real, and eigenvectors corresponding to distinct eigenvalues are orthogonal.
Detailed Explanation
Eigenvectors have several important properties that are useful in various applications. Firstly, if a matrix has 'n' different eigenvalues, then it will also have 'n' linearly independent eigenvectors, which provide a basis for the vector space. Secondly, although eigenvectors provide unique directions, they can be scaled, meaning that any non-zero multiple of an eigenvector is also an eigenvector. Furthermore, if a matrix has enough eigenvectors, it can be simplified into a diagonal form, which makes computations easier. For symmetric matrices, the eigenvalues are guaranteed to be real, and eigenvectors for different eigenvalues are orthogonal, which further aids in analysis.
Examples & Analogies
Consider a colorful kite flying in the wind. Each color represents a unique eigenvector that captures the kite's behavior in the wind (its direction). However, you can blow the kite harder or softer, thus changing its size while maintaining its shape (scaling). If you had multiple colorful kites, each representing a unique trajectory, together they would show you the entire beautiful array of how the kites navigate the air currents (the matrix's behavior).
Geometric Interpretation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An eigenvector represents a direction in which a linear transformation acts as a simple scaling, and the corresponding eigenvalue represents the scale factor. • If λ>1: Stretching • If 0<λ<1: Compression • If λ=−1: Reversal of direction • If λ=0: Maps to zero vector.
Detailed Explanation
Geometrically, eigenvectors can be seen as directions along which the transformation represented by the matrix acts as a simple scaling operation. The eigenvalue associated with an eigenvector indicates the type of scaling behavior. If the eigenvalue is greater than one (λ>1), the vector is stretched; if it is between zero and one (0<λ<1), the vector is compressed; if equal to -1 (λ=-1), the vector reverses direction; and if equal to zero (λ=0), the vector collapses to the zero vector.
Examples & Analogies
Imagine a rubber band that you stretch. If you pull it until it's twice as long (λ>1), you're stretching it; if you gently pinch it to about half its size (0<λ<1), it compresses. Reversing direction is like flipping the band so it snaps back the other way (λ=-1), and ultimately, if you cut the rubber band, it no longer exists (λ=0). Each of these changes represents a unique behavior similar to eigenvalues affecting eigenvectors during transformations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Eigenvalues: The scale factors related to eigenvectors in transformations.
-
Characteristic Equation: The polynomial used to derive eigenvalues from a matrix.
-
Diagonalization: The representation of a matrix through its eigenvectors and eigenvalues.
-
Mode Shapes: The deformations of structures during vibrational analysis determined by eigenvectors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For the matrix A = [[4, 2], [1, 3]], the characteristic polynomial is α^2 - 7α + 10 = 0, yielding eigenvalues λ = 5 and λ = 2.
-
In structural dynamics, the eigenvectors corresponding to these eigenvalues represent the mode shapes of how the structure deforms under load.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When multiplying a vector by A, Keep direction but change the way.
📖 Fascinating Stories
-
Once there was a flexible ruler named A, who could stretch and shrink any vector's way, turning it into a taller or shorter play, yet in the same direction, it would stay.
🧠 Other Memory Gems
-
Remember 'SCALE' for eigenvectors: Stretch, Compress, and Leave direction unchanged.
🎯 Super Acronyms
To remember key terms
- 'E-VECS' - Eigenvalues
- Vectors
- Eigenvectors
- Characteristic equation
- Scaling.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Eigenvector
Definition:
A non-zero vector that transforms into a scaled version of itself when multiplied by a matrix.
-
Term: Eigenvalue
Definition:
A scalar that indicates how much the eigenvector is stretched or compressed in the transformation.
-
Term: Characteristic Equation
Definition:
A polynomial equation derived from det(A - λI) = 0 used to find eigenvalues.
-
Term: Diagonalization
Definition:
The process of transforming a matrix into a diagonal matrix through its eigenvalues and eigenvectors.
-
Term: Mode Shape
Definition:
The shape of a structure's deformation during vibrational modes determined by eigenvectors.