Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Normalization
Unlock Audio Lesson
Today, we’re going to learn about normalizing eigenvectors. Can anyone tell me what normalization means in this context?
Does it mean making the vector have a length of one?
Exactly! Normalization scales the eigenvector so that its length or norm equals one. This is important in computations as it simplifies analysis and ensures consistency in results.
Why don't we always use normalized vectors?
Good question! While normalization is helpful, sometimes the original scaling of vectors contains crucial information, so it’s not always feasible. However, in many numerical methods, normalized vectors are preferred.
So, how do we normalize a vector?
We use the formula: \( v_{normalized} = \frac{v}{||v||} \). Who can tell me what \( ||v|| \) represents?
I think it’s the norm of the vector, like the length of it!
Correct! It measures the magnitude of the vector. Let's summarize: Normalizing an eigenvector helps in computational efficiency and accuracy. Can anyone suggest other benefits?
Applications of Normalized Eigenvectors
Unlock Audio Lesson
Now that we understand the basics of normalization, let's discuss its applications. How do you think normalized eigenvectors impact simulations in civil engineering?
It must make calculations faster and more stable.
Absolutely! Normalization leads to greater numerical stability, especially in systems involving a large number of equations or iterations. Does anyone have a specific example in mind?
In finite element analysis, right?
Yes! In finite element methods, normalized eigenvectors facilitate understanding deformation and stress patterns in structures. This allows engineers to avoid resonance in designs.
Is there a downside to this method?
Some practitioners may overlook the original vector scaling, which can lead to loss of context in certain applications. Balancing normalization with original data is key.
This makes sense. What should we take away from this?
Normalization enhances computational clarity and stability, making it essential for accurate simulations. Always consider the context of your eigenvectors!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Normalization of eigenvectors involves scaling them to unit length, which simplifies calculations and is especially beneficial in numerical simulations. This practice aids in achieving consistent results across various applications, allowing for easier interpretation of the eigenvector's significance.
Detailed
Normalization of Eigenvectors
In the process of working with eigenvectors, we often want to normalize them for several reasons. Normalization refers to the process of scaling a vector such that its length (or norm) is equal to one. The formula for normalizing an eigenvector \( v \) is given by:
\[ v_{normalized} = \frac{v}{||v||} \]
where \( ||v|| \) is the norm of the vector. This normalization is crucial in software tools and numerical simulations because it ensures stability, accuracy, and consistency across computations. By converting eigenvectors to a common scale, engineers and scientists can more effectively interpret their significance in various applications, such as structural analysis and vibration analysis. This section highlights the importance of normalized eigenvectors in enhancing clarity and precision in computational models.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Normalization of Eigenvectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eigenvectors are often normalized for ease of computation:
v
v =
norm ∥v∥
Detailed Explanation
Normalization is a process applied to eigenvectors to make them easier to work with in computations. When we normalize an eigenvector 'v', we ensure that its length (or magnitude) is equal to 1. This is done by dividing the vector by its norm (also called its length). The norm of 'v', denoted as ||v||, represents the square root of the sum of the squares of its components. The formula shows that after normalization, the new vector maintains the same direction as the original eigenvector but scales it down to a unit length.
Examples & Analogies
Imagine you're teaching someone how to shoot a basketball. You want them to focus on their aim and technique, so you tell them to stand at a distance of exactly 15 feet from the hoop - this is like normalizing their position for consistent practice. Similarly, normalizing an eigenvector ensures that every vector you work with has a 'standard size', making it easier to compare and calculate.
Importance of Normalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Especially useful in software tools and numerical simulations.
Detailed Explanation
Normalization is particularly important in computational fields, such as those used in engineering software. Many numerical methods rely on consistent and standardized inputs to function efficiently. For instance, when simulations are run in software, normalized eigenvectors can lead to faster calculations and improved accuracy, reducing errors that might arise from vectors of varying lengths. This standardization allows for clearer comparisons between vectors and simplifies the mathematical operations involved in simulations.
Examples & Analogies
Think of normalization as setting a standard volume level for music when sharing a playlist. If some songs are much louder than others, it becomes hard for listeners to enjoy them equally. By normalizing the sound levels, every song fits seamlessly into the listening experience. Similarly, normalizing eigenvectors gives a consistent format that benefits mathematical operations in engineering analyses.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Normalization: The process of scaling eigenvectors to have unit length for simplicity in computations.
-
Eigenvectors: Non-zero vectors that transform in a specific manner when multiplied by a matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
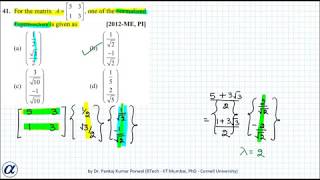
An example of normalizing an eigenvector \( v = [2, 4] \) gives \( v_{normalized} = \frac{[2, 4]}{\sqrt{20}} = [0.447, 0.894] \).
-
Normalization in a simplistic model makes the spectrum of a structural system clearer during vibration analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To keep vectors neat and tight, scale them down to unit height.
📖 Fascinating Stories
-
Imagine an engineer needing to measure building stability. They find vectors that are too long to compare, so they decide to 'normalize' for uniformity and easier understanding.
🧠 Other Memory Gems
-
N-E-A-T: Normalize Eigenvectors for Accurate Testing.
🎯 Super Acronyms
NORM
- Normalizing Optimizes Resulting Magnitudes.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Normalization
Definition:
The process of scaling a vector to have a length of one, ensuring consistent representation.
-
Term: Eigenvector
Definition:
A non-zero vector that changes only by a scalar factor when a linear transformation is applied.