Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Modal Analysis
Unlock Audio Lesson
Today we’ll discuss modal analysis, which is essential in determining how structures respond to dynamic loading. Can anyone tell me why it’s important for engineers?
It helps us understand how buildings or bridges will behave during events like earthquakes or heavy winds!
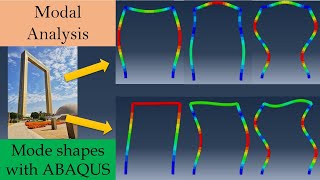
Exactly! Modal analysis identifies natural frequencies and mode shapes. These are crucial for ensuring the stability of large structures. What might happen if we ignore these factors?
We could end up designing something that fails under certain loads!
Well said! Remember, natural frequencies correspond to eigenvalues, and mode shapes correspond to eigenvectors. It's essential to grasp these connections for analyzing structures effectively.
Mathematical Formulation
Unlock Audio Lesson
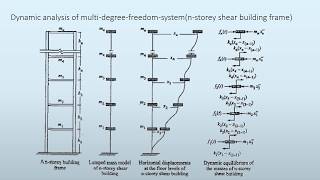
Let’s delve into the mathematics behind modal analysis. When we analyze a discretized beam, we typically start with the equation of motion, Mx¨ + Kx = 0. Can anyone explain what M and K represent?
M is the mass matrix and K is the stiffness matrix!
Exactly! To find the natural frequencies, we assume a solution of the form x(t) = ve^(iωt), leading us to a generalized eigenvalue problem, (K−ω²M)v=0. Why do we represent it this way?
It helps us express the dynamic characteristics of the structure in terms of eigenvalues and eigenvectors!
Correct! This transformation reveals critical insights into structural behavior. Understanding this relationship is key in applying modal analysis effectively.
Application of Modal Analysis in Civil Engineering Software
Unlock Audio Lesson
Now, let’s discuss how we apply these concepts in practice, particularly in civil engineering software like ETABS or ANSYS. How do you think engineers utilize modal analysis in these applications?
They probably use it to simulate how structures will behave under different load conditions!
Correct! These software tools utilize modal analysis to calculate natural frequencies and mode shapes, allowing engineers to predict potential issues before construction. Can anyone think of a scenario where this might be vital?
During an earthquake, understanding how a building will sway is crucial for safety.
Absolutely! Safety is the top priority in civil engineering. Modal analysis equips engineers with the necessary data to ensure that structures can withstand dynamic forces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers modal analysis in civil engineering structures like bridges and buildings, emphasizing its importance in dynamic loading scenarios. It details the use of natural frequencies as eigenvalues and mode shapes as eigenvectors, demonstrating how these concepts are mathematically explored using equations of motion.
Detailed
Modal Analysis in Structures
Modal Analysis is a critical aspect of civil engineering, particularly when examining how large structures such as bridges, buildings, and towers behave under dynamic loading conditions. In this section, we delve into the concepts of natural frequencies, which correspond to eigenvalues, and mode shapes, which correspond to eigenvectors. Through a mathematical framework, we’ll analyze how the equation of motion for a discretized beam or a building can be formulated as a generalized eigenvalue problem. This analysis is fundamental to predicting potential failures in structures and influences design decisions to enhance stability and safety. Modern engineering software like ETABS and ANSYS apply these principles to conduct simulations, allowing engineers to visualize structural behavior in response to dynamic forces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Importance of Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In large civil engineering structures (bridges, buildings, towers), it is often critical to understand how the structure behaves under dynamic loading. Modal analysis is used to find:
- Natural frequencies (eigenvalues),
- Mode shapes (eigenvectors).
Detailed Explanation
Modal analysis is a technique used to study how structures respond to dynamic loads, such as those from earthquakes, winds, or vibrations. Understanding how a structure behaves under these conditions is crucial for ensuring its safety and durability. In this context, natural frequencies are the specific frequencies at which a structure tends to oscillate, whereas mode shapes describe the pattern of motion associated with each natural frequency. These concepts are essential for predicting how structures will respond when subjected to various forces.
Examples & Analogies
Imagine a swing at a playground. When you push the swing, it moves back and forth at certain natural frequencies. If you push it at just the right moment, it swings higher. This is similar to how a building might sway during an earthquake; understanding its natural frequencies allows engineers to design structures that can move with the forces rather than against them, preventing damage.
Mathematical Formulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example:
Consider a discretized beam or building with mass M and stiffness K. The equation of motion is:
Mx¨ + Kx = 0
To solve this, assume x(t) = veiωt, substitute into the equation:
(K - ω²M)v = 0
This is a generalized eigenvalue problem, with ω² as eigenvalues and v as eigenvectors (mode shapes).
Detailed Explanation
In this section, we see a mathematical example of how to implement modal analysis using a simplified model of a building or beam. The equation Mx¨ + Kx = 0 represents the motion of the structure, where M is the mass matrix and K is the stiffness matrix. By assuming a solution form (x(t) = ve^(iωt)), we find the eigenvalues and eigenvectors, leading to the eigenvalue problem (K - ω²M)v = 0. This relationship helps identify how different parts of the structure will move (mode shapes) at specific frequencies (natural frequencies).
Examples & Analogies
Think of a guitar string. When plucked, it vibrates at certain frequencies to produce sound. If the string is too tight or too loose, it won't vibrate correctly, producing a different (and often unpleasant) sound. Similarly, in a building, if the structural components are not correctly designed for their natural frequencies, the building may sway excessively during an earthquake, leading to potential collapse.
Software Utilization in Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Software like ETABS, STAAD.Pro, or ANSYS uses this process internally.
Detailed Explanation
Modern engineering software tools implement modal analysis calculations automatically, which simplifies the analysis for engineers. By inputting the structure's parameters, the software can quickly calculate the natural frequencies and mode shapes, providing valuable insights without manual calculations. These tools utilize the same principles discussed, but automate the complex mathematics involved, allowing for faster and more reliable design processes.
Examples & Analogies
Consider cooking with a pressure cooker that has a specific safety valve. Engineers can think of modal analysis software as a ‘safety valve’ for structures. It takes countless variables into account and processes them rapidly, ensuring the design can handle dynamic loads, just like the safety valve ensures that the pressure does not exceed safe levels in cooking.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Natural Frequencies: The rates of vibration of a structure, represented as eigenvalues.
-
Mode Shapes: The patterns of deformation for structures under load, represented as eigenvectors.
-
Dynamic Loading: Forces or motions that change with time, necessitating modal analysis.
-
Generalized Eigenvalue Problem: A mathematical formulation defining the relationship for dynamic systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a bridge analyzed using modal analysis to predict its response to an earthquake by calculating its natural frequencies.
-
The simulation of a large building under wind loads, utilizing software tools to perform modal analysis and to assess stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When structures sway and twist, modes of motion can't be missed.
📖 Fascinating Stories
-
Imagine a tall tower swaying in the wind. It moves in specific patterns or 'modes' that show how it withstands the force. Engineers study these to make sure it doesn’t tumble!
🧠 Other Memory Gems
-
To remember the key elements of modal analysis, think 'M(E)AS: Mass, Eigenvalue, Analysis, Structure'.
🎯 Super Acronyms
Use 'FAME' for frequency, analysis, mass, and eigenvalues in modal study.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Modal Analysis
Definition:
A method in engineering used to determine the natural frequencies and mode shapes of a system, especially structures under dynamic loads.
-
Term: Natural Frequencies
Definition:
The eigenvalues associated with a system that indicate the rates at which it vibrates.
-
Term: Mode Shapes
Definition:
The eigenvectors corresponding to natural frequencies, depicting the deformation pattern of a structure under dynamic loading.